引言

在Matlab实现小世界网络生成及其分析中，我们已经讨论了社会网络结构属性以及小世界网络的生成算法、结构分析。
在该文中，我们提到社会网络最重要的三个属性是：

群聚系数
平均路径长度
节点度分布

通过小世界网络生成算法能够很好地研究群聚系数和平均路径长度对网络信息传递的影响。
因此，本文将从无标度网络出发，研究网络结构度分布的特点。

社会网络分类

在发现万维网的度服从非泊松分布之前，人们通常认为复杂网络的节点度服从泊松分布 [1]。而实际上许多真实的网络结构，如学术论文的引用关联网络 [2]的节点度并不服从泊松分布，而是服从如下图所示的幂律分布 [3]。
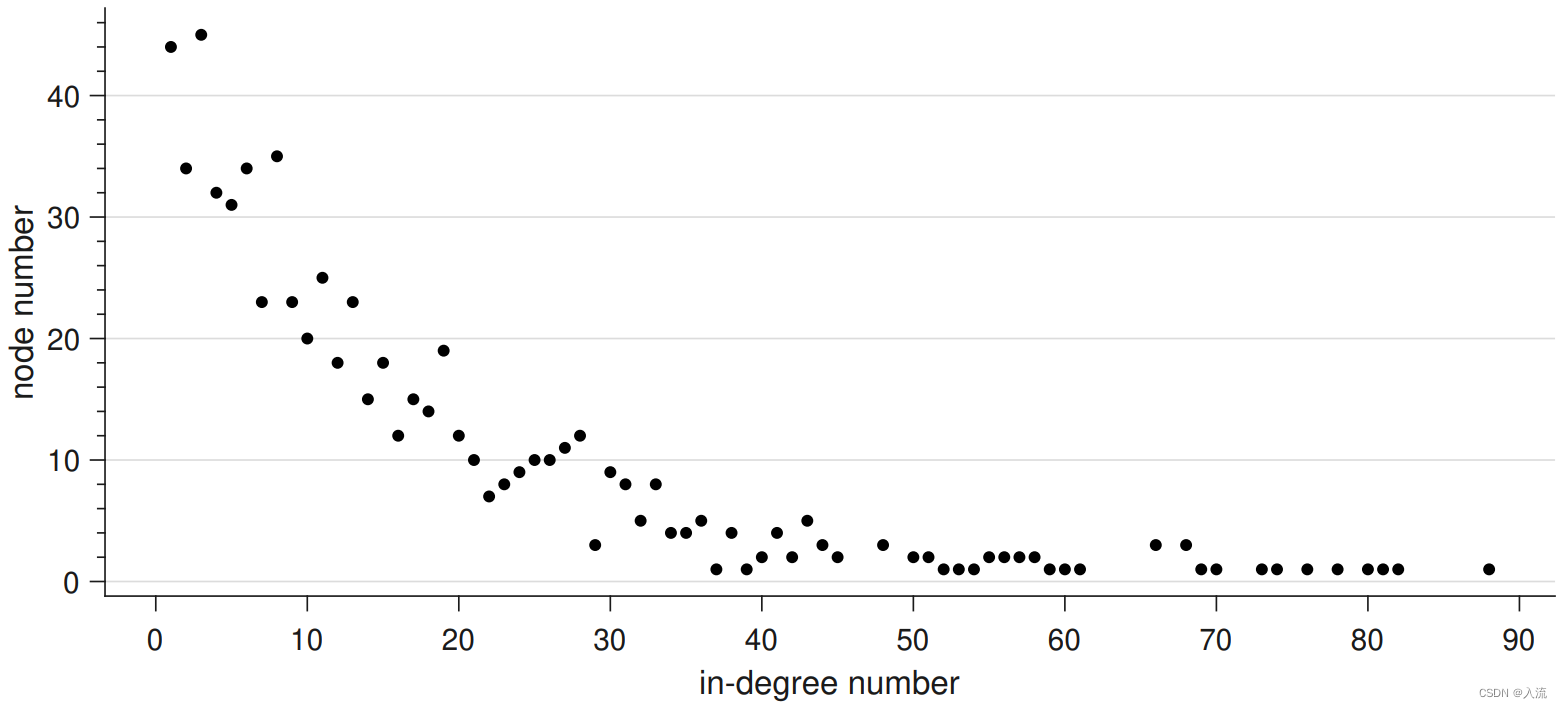
幂律分布图

因此，根据真实网络的节点度分布将“小世界”网络进一步划分为以下三类[4]：

1） scale--free networks：节点的度分布呈现出幂律衰减的特征；
2） broad--scale networks：节点的度分布呈现出幂律衰减的特征，但存在着一个指数截断现象；
3） single--scale networks：节点的度分布呈现出指数衰减的特征。

这里的scale--free networks即为无标度网络。该类网络中的大多数节点都拥有很少的边连接数，只有少数网络节点的相连节点度很大。这些连接度很大的节点在网络信息传递中扮演着主导作用 [5]。
文献 [3] 提出了节点增加和连接偏好两种机制来解释这类度很大的节点出现的原因。该连接偏好机制认为：“对于网络中的已有节点 $i$ ，其被新增节点连接的概率 $p_i$ 与它的节点度 $k_i$ 呈正比例关系。”。这一概率可以用下式表示：
$p_i = \frac{k_i}{\sum_j{k_j}}$
在上式中，分母项 $\sum_j{k_j}$ 表示的是当前所有节点的度数总和。

Barabási-Albert无标度网络生成算法

基于节点增加和连接偏好，Barabási 和 Albert提出了一类无标度网络生成算法。具体算法流程图如下：
在这里插入图片描述

MATLAB代码实现

这里提供了两类生成代码（均来自网上开源代码）

无向的无标度网络生成代码BAgraph_undir

function [sparsematrix, fullmatrix] = BAgraph_undir(N,m0,m)
adjacent_matrix = sparse( m0, m0);% 初始化邻接矩阵
for i = 1: m0
    for j = 1:m0
        if j ~= i      %去除每个点自身形成的环
            adjacent_matrix(i,j) = 1;%建立初始邻接矩阵，3点同均同其他的点相连
        end
    end
end
adjacent_matrix =sparse(adjacent_matrix);%邻接矩阵稀疏化
node_degree = zeros(1,m0+1);                %初始化点的度
node_degree(2: m0+1) = sum(adjacent_matrix);%对度维数进行扩展
for iter= 4:N
    iter;                               %加点
    total_degree = 2*m*(iter- 4)+6;%计算网络中此点的度之和
    cum_degree = cumsum(node_degree);%求出网络中点的度矩阵
    choose= zeros(1,m);%初始化选择矩阵
    % 选出第一个和新点相连接的顶点
    r1= rand(1)*total_degree;%算出与旧点相连的概率
    for i= 1:iter-1
        if (r1>=cum_degree(i))&&( r1<cum_degree(i+1))%选取度大的点
            choose(1) = i;
            break
        end
    end
    % 选出第二个和新点相连接的顶点
    r2= rand(1)*total_degree;
    for i= 1:iter-1
        if (r2>=cum_degree(i))&&(r2<cum_degree(i+1))
            choose(2) = i;
            break
        end
    end
    while choose(2) == choose(1)%第一个点和第二个点相同的话，重新择优
        r2= rand(1)*total_degree;
        for i= 1:iter-1
            if (r2>=cum_degree(i))&&(r2<cum_degree(i+1))
                choose(2) = i;
                break
            end
        end
    end
    % 选出第三个和新点相连接的顶点
    r3= rand(1)*total_degree;
    for i= 1:iter-1
        if  (r3>=cum_degree(i))&&(r3<cum_degree(i+1))
            choose(3) = i;
            break
        end
    end
    while (choose(3)==choose(1))||(choose(3)==choose(2))
        r3= rand(1)*total_degree;
        for i=1:iter-1
            if (r3>=cum_degree(i))&&(r3<cum_degree(i+1))
                choose(3) = i;
                break
            end
        end
    end
    %新点加入网络后, 对邻接矩阵进行更新
    for k = 1:m
        adjacent_matrix(iter,choose(k)) = 1;
        adjacent_matrix(choose(k),iter) = 1;
    end
    node_degree=zeros(1,iter+1);
    node_degree(2:iter+1) = sum(adjacent_matrix);
end
sparsematrix = adjacent_matrix;
% tu_plot(matrix,0);%画出当前的连接图
fullmatrix=full(adjacent_matrix);%得到邻接矩阵
%将主对角元素也记为1，即认为自己也属于邻居一员
for i=1:N
    fullmatrix(i,i)=1;
end
end

有向的无标度网络生成代码BAgraph_dir

function retAdjMat = BAgraph_dir(N,mo,m)
% Generates a scale-free directed adjacency matrix using Barabasi and Albertalgorithm
% Input: N - number of nodes in the network, mo - size of seed, m = average degree. 
% Use mo=m or m<mo.
% Example: A = BAgraph(300,10,10);
% Ref: Methods for generating complex networks with selected structural properties for simulations, Pretterjohn et al, Frontiers Comp Neurosci

% Author:
% Tapan P Patel, Ph.D., tapan.p.patel@gmail.com
% University of Pennsylvania
hwait = waitbar(0,'Please wait. Generating directed scale-free adjacency matrix');
A = zeros(N);
E = 0;
for i=1:mo
	for j=i+1:mo
		
		A(i,j) =1;
		A(j,i) = 1;
		E = E + 2;
	end
end
% Second add remaining nodes with a preferential attachment bias - rich get
% richer
for i=mo+1:N
	waitbar(i/N,hwait,sprintf('Please wait. Generating directed scale-free adjacency matrix\n%.1f %%',(i/N)*100));
	curr_deg =0;
	while(curr_deg<m)
		sample = setdiff(1:N,[i find(A(i,:))]);
		j = datasample(sample,1);
		b = sum(A(j,:))/E;
		r = rand(1);
		if(b>r)
			r = rand(1);
			if(b>r)
			A(i,j) = 1;
			A(j,i) = 1;
			E = E +2;
			else
			A(i,j) = 1;
			E = E +1;
			end
		else
			no_connection = 1;
			while(no_connection)
				sample = setdiff(1:N,[i find(A(i,:))]);
				h = datasample(sample,1);
				b = sum(A(h,:))/E;
				r = rand(1);
				if(b>r)
					r = rand(1);
					if(b>r)
					A(h,i) = 1;
					A(i,h) = 1;
					E = E +2;
					else
					A(i,h) = 1;
					E = E+1;
					end
					no_connection = 0;
				end
			end
		end
		curr_deg = sum(A(i,:));
	end
end
retAdjMat = A;
waitbar(1,hwait,'Successfully generating onn B-A scale free graph');
pause(1)
delete(hwait);
end

无标度网络的节点度统计分析

对于生成得到的有向或无向的无标度网络G。我们可以在得到其邻接矩阵adjMat的基础上，直接统计行和和列和作为网络的入度及出度，并人为的进行曲线拟合。

无向的无标度网络节点频率统计算法

%% 本脚本将被用于绘制一个网络的度分布图
% 只适用于无向图的邻接矩阵，若要绘制有向图的邻接矩阵，请参考plotDirDegDistribution
function plotDegDistribution(adjMat,type)
% Input：
% 1. adjMat: 一个网络结构图的邻接矩阵
% 2. type: 绘制的曲线图类型，缺省情况下为曲线图
% 只能用于无向图，因此要求传入的邻接矩阵是对称的
if nargin < 2
    type = '-';
    disp('默认绘制曲线图，而不是散点图');
end
row = size(adjMat,1);
col = size(adjMat,2);
assert(row==col, '邻接矩阵必须是一个方阵'); % 输入检测限制
assert(all(all(adjMat==adjMat'))==1, '必须是无向图的邻接矩阵，即对称');
degree = sum(adjMat);
degCase = unique(degree); % 计算度的种类个数
degFreq = zeros(length(degCase),2); % 构造一个键值对
degFreq(:,1) = degCase; % 设置键值
for i=1:length(degCase)
    degFreq(i,2) = sum(sum(degree == degCase(i))); % 统计节点度的频率
end
figure % 绘制幂律
loglog(degFreq(:,1),degFreq(:,2),type);
set(gcf,'Color','w');
figure % 绘制普通坐标
plot(degFreq(:,1),degFreq(:,2),type);
set(gcf,'Color','w');
maxFreq = max(degFreq(:,2));
maxIdx = max(degFreq(:,1)); % 统计坐标范围
xticks(0:5:(ceil(maxIdx/5)*5));
yticks(0:20:(ceil(maxFreq/20)*20));
ylim ( [-5 ceil(maxFreq/20)*20]);
xlim ([0 (ceil(maxIdx/5)*5)+3]);
xlabel('Node degree value');
ylabel('Degree frequency');
end

有向的无标度网络节点频率统计算法

%% 本脚本将被用于绘制一个网络的度分布图
% 只适用于有向图的邻接矩阵，若要绘制无向图的邻接矩阵，请参考plotDegDistribution
function plotDirDegDistribution(adjMat,type)
% Input：
% 1. adjMat: 一个无向网络结构图的邻接矩阵
% 2. type: 绘制的曲线图类型，缺省情况下为曲线图
% 只能用于有向图，因此要求传入的邻接矩阵是对称的
if nargin < 2
    type = '-';
    disp('默认绘制曲线图，而不是散点图');
end
row = size(adjMat,1);
col = size(adjMat,2);
assert(row==col, '邻接矩阵必须是一个方阵'); % 输入检测限制

%% 统计节点度
inDegree = sum(adjMat,1); 
outDegree = sum(adjMat,2);
totalDegree = inDegree + outDegree'; 
degCase = unique(totalDegree); % 计算度的分布
degFreq = zeros(length(degCase),2);
degFreq(:,1) = degCase; % 构造一个键值对，键为度的种类，值为度的频次
for i=1:length(degCase)
    degFreq(i,2) = sum(totalDegree == degCase(i)); % 统计节点度的频率
end
figure % 绘制幂律
loglog(degFreq(:,1),degFreq(:,2),'o');
set(gcf,'Color','w');
figure % 绘制普通坐标
plot(degFreq(:,1),degFreq(:,2),'o');
set(gcf,'Color','w');
maxFreq = max(degFreq(:,2));
maxIdx = max(degFreq(:,1)); % 统计坐标范围
xticks(0:5:(ceil(maxIdx/5)*5));
yticks(0:20:(ceil(maxFreq/20)*20));
ylim ( [-5 ceil(maxFreq/20)*20]);
xlim ([0 (ceil(maxIdx/5)*5)+3]);
xlabel('Node degree value');
ylabel('Degree frequency');
end

完整的分析代码

在网络结构生成算法以及网络节点度统计分析算法都实现以后，可以实现一个完整的分析流程。

请将这些代码分别用.m保存，然后文件名命名为对应的函数名。

在这里插入图片描述

代码实现

%% 脚本说明：本脚本将被用于分析B-A无标度网络
% 主要用于分析：网络的节点度分布情况
% 依赖的外部脚本包括：
% 1. 生成有向的无标度网络的脚本：BAgraph_dir(N,mo,m)
% 2. 绘制节点分布图的脚本：plotDegDistribution
% 特别地，还需要工具箱cftool
%% 参数初始化
clear;
N = 200; % 网络的节点总数
m0 = 5; % 初始节点数
m = 5; % 每个新增节点带来的边数增加
assert(m <= m0 && N >= m0, '参数m必须小于等于初始节点数，不然会出现重复边或自环');
%% 生成有向的BA无标度模型的图
retAdjMat = BAgraph_dir(N,m0,m); % 得到的是矩阵
%% 网络结构可视化
retGraph = digraph(retAdjMat); 
plot(retGraph,'NodeColor','k','EdgeAlpha',0.3);
title(['ScaleFree Graph with N =', num2str(N),' nodes, m0 = ' num2str(m0), ' and m = ', ...
    num2str(m)], 'Interpreter','latex')
axis off;
set(gcf, 'Color', 'w');
% 通过脚本有向的无标度网络的度分布图
plotDirDegDistribution(retAdjMat,'o');

这段代码主要是对由BAgraph_dir生成的有向无标度网络进行度分布统计并可视化工作。
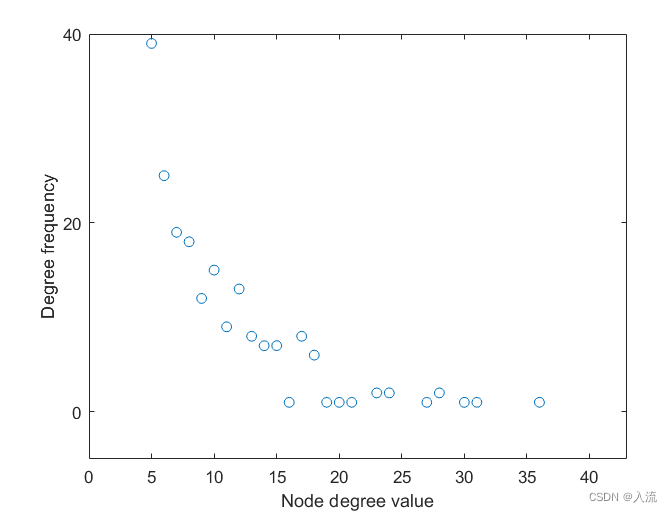
在这里插入图片描述
从上图也可以发现：节点度呈现出幂律分布的趋势。但这样可视化的效果不是很好。因此，在得到节点度分布degCase及对应频次degFreq的基础上，我们可以通过matlab的曲线拟合工具cftool得到更为好看的曲线拟合图。

直接调用命令cftool（这里不确定是否需要手动安装该工具箱）

%% 通过工具箱cftool进行曲线拟合，需要选取对应的数据
cftool; % 进行曲线拟合

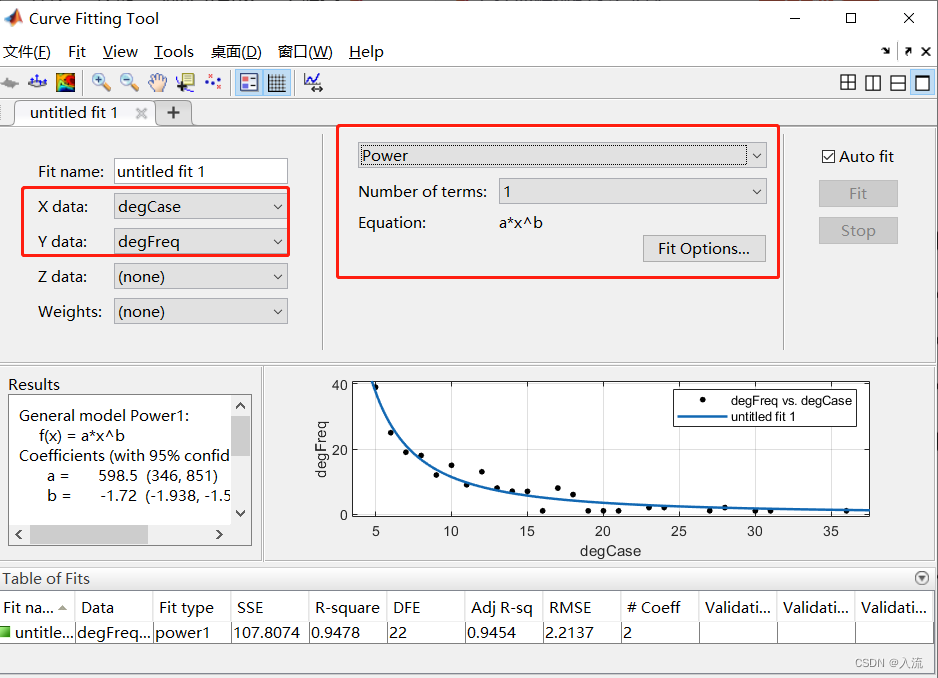
在这里插入图片描述
还可以对这一拟合后的figure进行编辑。

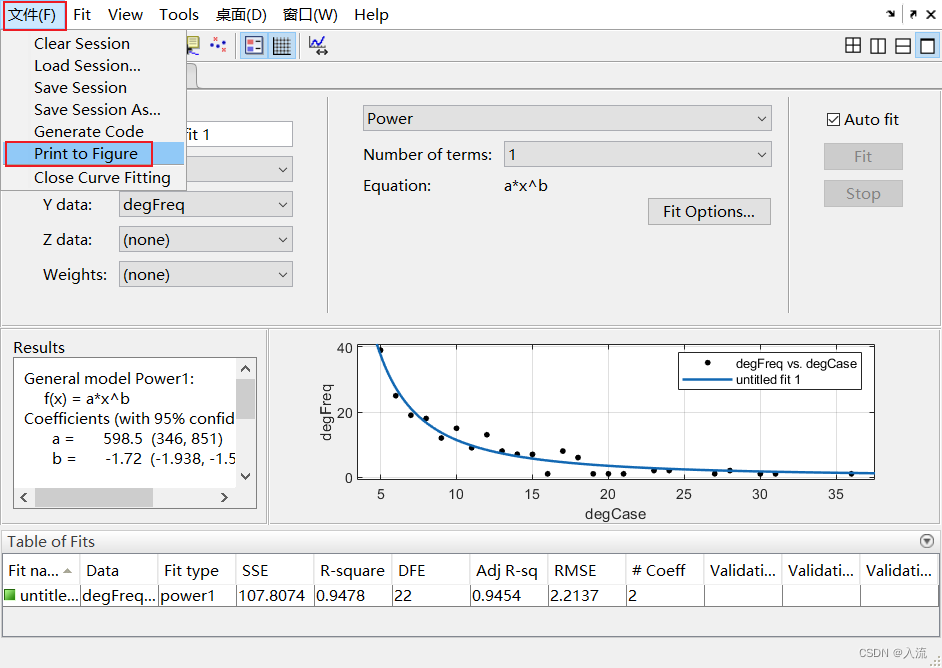
总结

Matlab实现小世界网络生成及其分析和这篇文章对小世界网络及无标度网络的生成算法、结构分析做了一个比较充足的讨论。也提供了一些可视化的代码实现。

在Matlab中，我们倾向于得到一个矩阵的邻接矩阵，进而进行相应的分析工作。
而实际上，matlab对于graph这一对象的支持也做的很完善。可以通过命令doc grpah查看完整的帮助。
在这里插入图片描述
这里就不仔细为大家分析了。

参考文献

[1] Albert-László, Barabási. Scale-free networks: a decade and beyond.[J]. Science (New York,N.Y.), 2009, 325(5939): 412--413
[2] Redner, S… How popular is your paper? an empirical study of the citation distribution[J]. Physics of Condensed Matter, 1998, 4(2)
[3] A.-L. Barabási, R. Albert. Emergence of scaling in random networks[J]. science, 1999, 286(5439): 509--512
[4] L. Amara, A. Scala, M. Barthelemy, et al. Classes of small-world networks[J]. , 2011, 207--210
[5] Q. Zha, G. Kou, H. Zhang, et al. Opinion dynamics in finance and business: a literature review and research opportunities[J]. Financial Innovation, 2020, 6(1): 1--22