[数据结构与算法]PID控制算法学习与Matlab仿真

起因

PID控制算法应该是包括工业机器人等各种行业和领域中非常常用的一种控制算法了。了解这个算法的起因是在稚晖君开发的自行车项目中见到，后来在北理工组会中了解到PID控制算法属于控制工程专业中非常基础的理论。
初步了解之后就会经常注意到这个算法，发现PID在飞控算法中非常重要，也常出现在b站分享的各种自平衡项目中。前两天又了解到著名“载人航天仿真工程软件”《坎巴拉太空计划》的MOD中也可以通过写入PID算法来对火箭姿态进行控制。可以说此算法是既实用又很酷了。

算法原理

连续系统中的PID算法公式如下
$$\begin{gathered} U(t)=k_P\left[err(t)+\frac{1}{T_I}\int err(t)dt+T_D\frac{d[err(t)]}{dt}\right] \\ =k_{P}err(t)+\frac{k_P}{T_I}\int err(t)dt+T_D{k}_P\frac{d[err(t)]}{dt} \\ =k_{P}err(t)+k_I\int err(t)dt+k_D\frac{d[err(t)]}{dt} \end{gathered}$$
其中$U(t)$即为调节的控制量，$err(t)$为期望值与实际值的偏差，由于实际使用时都要对三个参数进行调节，因此索性直接写为$k_P$$k_I$$k_D$，正好代表了P比例 I积分 D微分三个调节参数。
离散系统中的PID算法公式如下
$$U(t)=K_{P}err(t)+K_I\sum _{n=0}^{k}err(n)+K_D\left[err(k)?err(k?1)\right]$$
算法结构如下

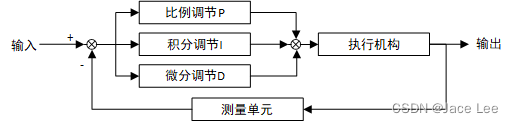
算法解析

比例P就是常规中很直觉的控制思想，即大了就缩小，小了就扩大；

比例P存在的问题是调节速度过快会引起系统在期望值处震荡，因此引入微分D；
微分D考量变化速度，若变化速度过大将降低调节量；

比例P+微分D存在的问题是，存在稳态误差（系统由于其他干扰，使得比例调节无法完成期望值，在另一处实现稳态），因此引入积分I；
积分I考量一段时间的误差积累（特别是稳态误差），根据误差积累改变调节量。

调参小技巧

最优的曲线貌似因人而异，如果需要更快达到目标，可以存在少量超调，微微震荡，如果对震荡敏感，可以严格限制超调，降低达到目标的速度，总的来说：

1. 先$K_p$后$K_i$最后$K_d$；
2. 确定$K_p$ 时，由0逐渐加大比例增益$K_p$，直至系统出现振荡，再从此时的比例增益$K_p$逐渐减小，直至系统振荡消失，记录此时的比例增益$K_p$，设定最终的比例增益$K_p$为当前值的60%~70%；
3. $K_i$也一样保证在震荡的临界处即可；
4. 最后加$K_d$。

Matlab仿真

%Project: 【PID控制算法仿真】最简单的系统
%Author: Jace
%Data: 2022/6/12
%====================准备====================
clear all;
close all;
clc;
%====================初始化参数====================
%--------全局参数--------
N=100;
%--------系统模型参数1--------
A=0.9;
B=0.2114;

%--------分配空间--------
x=zeros(1,N);
u=zeros(1,N);
e=zeros(1,N);
Sum_e=zeros(1,N);
r=zeros(1,N);

%--------初始化--------
r(1)=800;
x(1)=0;
e(1)=0;   
Sum_e(1)=0;

%--------PID参数--------
% kp=0.22;    
% ki=0.13;
% kd=0;
kp=2;    
ki=0.23;
kd=0.2;
for k=2:N
    %系统运行
    x(k)=A*x(k-1)+B*u(k-1)+B*u(k);%系统状态方程
    if k<N/2
        r(k)=r(1);%期望值
    else
        r(k)=r(1)-200;
    end
    e(k)=r(k)-x(k);%误差信号
    Sum_e(k)=Sum_e(k-1)+e(k);%误差的累加和
    u(k)=kp*e(k)+ki*Sum_e(k)+kd*(e(k)-e(k-1)); %PID控制器输出
end

figure;
hold on,box on;
plot(x,'-r.');
plot(r,'-k.');
legend('State','Expect');
axis([0 N 0 1000])
xlabel('Sampling Time');ylabel('Value');
title('State');