[数据结构与算法]选择 & 冒泡 & 快速排序算法详解

这边文章主要介绍选择、冒泡和快速排序算法上面，相信大家对前两种算法都是很熟悉的了，特别是冒泡排序，这三种算法也是递进的关系， 需要了解插入、希尔、归并排序算法的请看我另外一篇文章。

选择排序

场景：如果我们要找到公司里薪资最高的人你会怎么找？
选择排序的思路跟插入排序是非常相似的，也分已排序区间和未排序区间，但选择排序每次会从未排序区间找到最小的元素，将其放到已排序区间的末尾，但是插入排序是移动数组，选择排序是进行交换，例如以下例子：
6000 8000 5000 9000 4000
第一次：4000 6000 8000 5000 9000
第二次： 4000 5000 6000 8000 9000
代码实现：

public static void chooseSort(int[] num){
        for (int i = 0; i < num.length; i++) {
            for (int j = i+1; j < num.length; j++) {
                if (num[i]>num[j]){ //将小的数据移动到前面来
                    num[i]=num[i]+num[j];
                    num[j]=num[i]-num[j];
                    num[i]=num[i]-num[j];
                }
            }
        }
        System.out.println(Arrays.toString(num));
    }

可以看到选择排序是需要遍历n*n次数组的 所有时间复杂度为O(N2) ，空间复杂度为O(N)，稳定性肯定是不稳定的。

冒泡排序

核心思想：冒泡排序是操作相邻的两个数，每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系，如果不满足，就交换两个位置的元素。一次冒泡至少会让一个元素移动到它应该在的位置，重复n次，就完成n个数据的排序工作
举例说明：4 5 6 3 2 1,从小到大排序。
1 2 3 4 5 6进行排序：什么样的情况下不做任何交换了呢，那就是所有的数都在它应该在的位置；O(n)
第一次冒泡的结果:4 5 6 3 2 1->4 5 3 6 2 1 - > 4 5 3 2 6 1 -> 4 5 3 2 1 6,哪个元素的位置确定了，6
第二次冒泡的结果:4 5 3 2 1 6->4 3 5 2 1 6 -> 4 3 2 5 1 6 -> 4 3 2 1 5 6
第三次冒泡的结果:4 3 2 1 5 6->3 4 2 1 5 6 -> 3 2 4 1 5 6 -> 3 2 1 4 5 6
第四次冒泡的结果:3 2 1 4 5 6->2 3 1 4 5 6 -> 2 1 3 4 5 6
第五次冒泡的结果:2 1 3 4 5 6->1 2 3 4 5 6
代码实现：

public static void bubbleSort(int [] nums){
        int n=nums.length;
        for (int in = 0; in<n-1 ; in++) { //最后一次排序不需要
            boolean flag=false; //如果遍历一次 所有的数据都没有做交换 说明数据本身就是排好序的
            for (int i = 0; i <n-in-1 ; i++) {
                if (nums[i]>nums[i+1]){
                    nums[i]=nums[i]+nums[i+1];
                    nums[i+1]=nums[i]-nums[i+1];
                    nums[i]=nums[i]-nums[i+1];
                    flag=true;
                }
            }
            if(!flag) break; //数组是个有序数组 直接返回就好了
        }
        System.out.println(Arrays.toString(nums));
    }

冒泡排序时间复杂度最坏的情况还是需要遍历n*n次数组，时间复杂度为O(N2），空间复杂度为O(N），稳定性是稳定的。

快速排序

快速排序的思想结合了递归，回溯，以及双指针的思想。
核心思想：首先选择一个基准数，从后面往前找到比基准数小的数进行交换，从前往后找比基准数大的数进行交换，这时候数组就分为三个部分，左边的比基准数小，右边比基准数大，然后左右两边在进行上述操作。例如：
45 28 80 90 50 16 100 10
基准数：一般就是取要排序序列的第一个。
第一次排序基准数：45
从后面往前找到比基准数小的数进行对换：
10 28 80 90 50 16 100 45
从前面往后面找比基准数大的进行对换：
10 28 45 90 50 16 100 80

10 28 16 90 50 45 100 80
10 28 16 45 50 90 100 80
以基准数分为3部分，左边的比之小，右边比之大：
{10 28 16} 45 {50 90 100 80}
到此第一次以45位基准数的排序完成。
然后再将左右两边的数组选取基准数，在进行对比交换，就能完成排序

流程图：

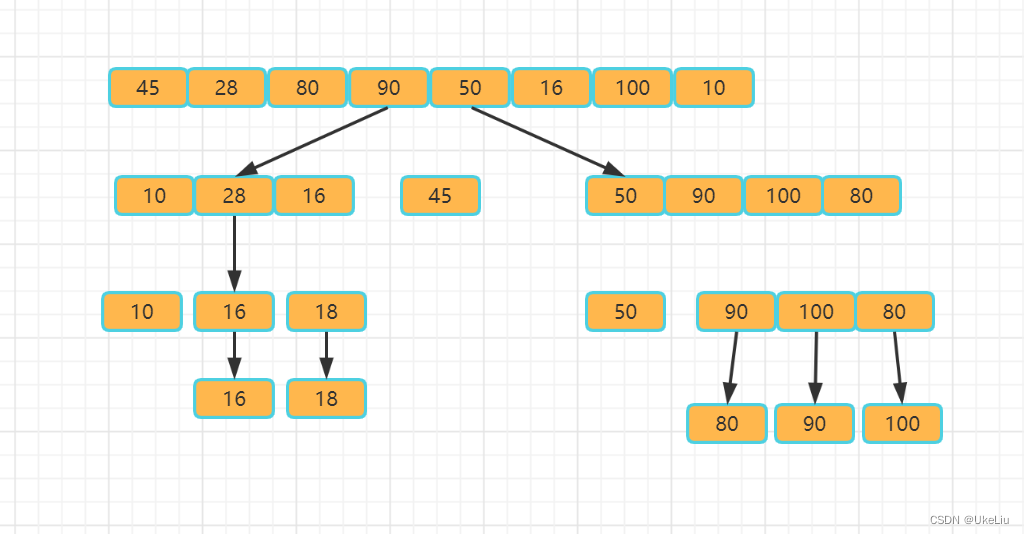
代码实现：

 public static void QuickSort(int[] num){
        int left=0;
        int right=num.length-1;
        //进行第一次排序
        quickChild(num,left,right);
    }

    public static void quickChild(int[] num,int ll,int rr){
        int base=num[ll]; //基准数
        int left=ll; //左指针
        int right=rr; //右指针
        while (left<right){
            //从后面往前找比基准数小的数
            while (left<right && num[right]>base){
                right--;
            }
            if (left<right){
                num[left]=num[left]+num[right];
                num[right]=num[left]-num[right];
                num[left]=num[left]-num[right];
                left++;
            }
            //从前往后找 找到比基准数大的数
            while (left<right && base>num[left]){
                left++;
            }
            if (left<right){
                num[left]=num[left]+num[right];
                num[right]=num[left]-num[right];
                num[left]=num[left]-num[right];
                right-- ;
            }
        }
        //现在数组分成了三个部分 左右再继续进行快排 使用递归
        if (ll<left) 
        quickChild(num,ll, left-1);
        if (left<rr)
        quickChild(num,left+1, rr);
    }

快速排序的时间复杂度O（nlogn），最坏的情况还是O（n2），空间复杂度是O（n），稳定性是不稳定的。
快速排序和归并排序的算法的比较：

1. 归并排序的处理过程是由下往上的，先处理子问题，然后在合并。
2. 快排其实就是从上往下，先分区，在处理子问题，不用合并，分区的同时将大小比较了
3. 快速排序的优化思想就是要找对基准数，基准数在中间，就是最好的

总结一下：

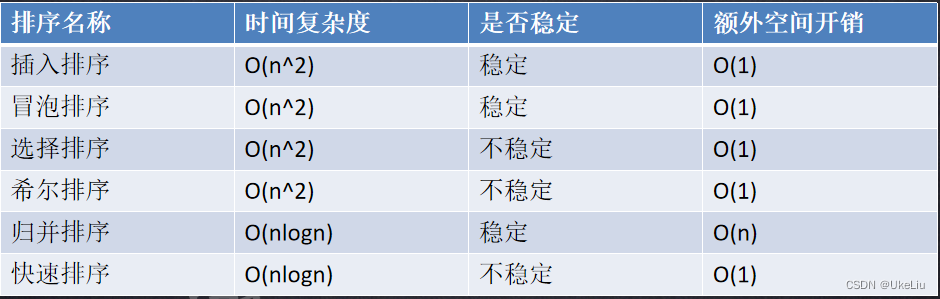
这里给大家提供一下算法选择的思路，

1. 如果你的数据量很小的话，这样就不用考虑归并和快速，直接用插入和选择等简单的算法就行，因为数据量小，其中的时间复杂度完全可以忽略不计。
2. 分析你的存储空间，归并的话会有额外的空间开销，如果你的空间有限，就是用快排，如果空间多的话，你都可以考虑。
3. 分析你的数据量，如果你的数据量在不断的增加或者数据量大，建议还是用归并和快速，虽然前期数据量小，可能使用插入等算法会快一点，但是到后期数据量越来越大，就会越来越慢，只有去升级代码了。
4. 分析你的场景，比如你要根据订单的下单时间以及下单的金额进行排序，你的时间必须是从前往后，那你的排序算法就要稳定的，这时候你只能选择稳定的排序算法。

在这里我只讲解了六种简单的算法，当然还有很多巧妙的算法，我们只有不停的去学习，才能在需要的时候使用好他们。