排序算法的执行效率
排序算法的执行效率一般从以下几个角度衡量
- 最好情况、最快情况、平均情况下的时间复杂度
- 时间复杂度的系数、常数 、低阶
- 比较次数和交换(或移动)次数
排序算法的内存消耗
算法的内存消耗是靠空间复杂度来衡量。在排序算法中有一个新的概念叫做 原地排序,原地排序就是特制空间复杂度是O(1)的算法。
排序算法的稳定性
排序算法中还有一个重要的度量指标:稳定性 指的是,如果带排序的数据中有两个相等的元素,排序完成后两个相等元素的原有的前后顺序不变。比如 3,2,5,4,3 。按照大小排序后是:2,3,3,4,5 .稳定排序就是指排完之后,第一个3仍然在第二个三前面。
**稳定排序的意义:**一个实际的例子,一个订单列表要按照相同的订单金额从小到大排序,相同金额的订单按照创建时间排序。一般的思路先按照订单金额排序,然后处理金额相等的一段一段的时间,思路简单,但是实现起来有点复杂。
简单点的:先按照订单时间排序,然后再使用稳定排序对订单金额排序,这样相同金额的订单,创建时间也是从小到大了。
冒泡排序(Bubble Sort)
冒泡排序只会操作相邻的连个数据。每次冒泡操作都会对相邻的两个元素进行比较,如果不满足大小关系就将他们交换。一次冒泡至少会让一个元素移动大他应该在的位置,重复n次就完成了n个数据的排序工作。
冒泡排序示意图:
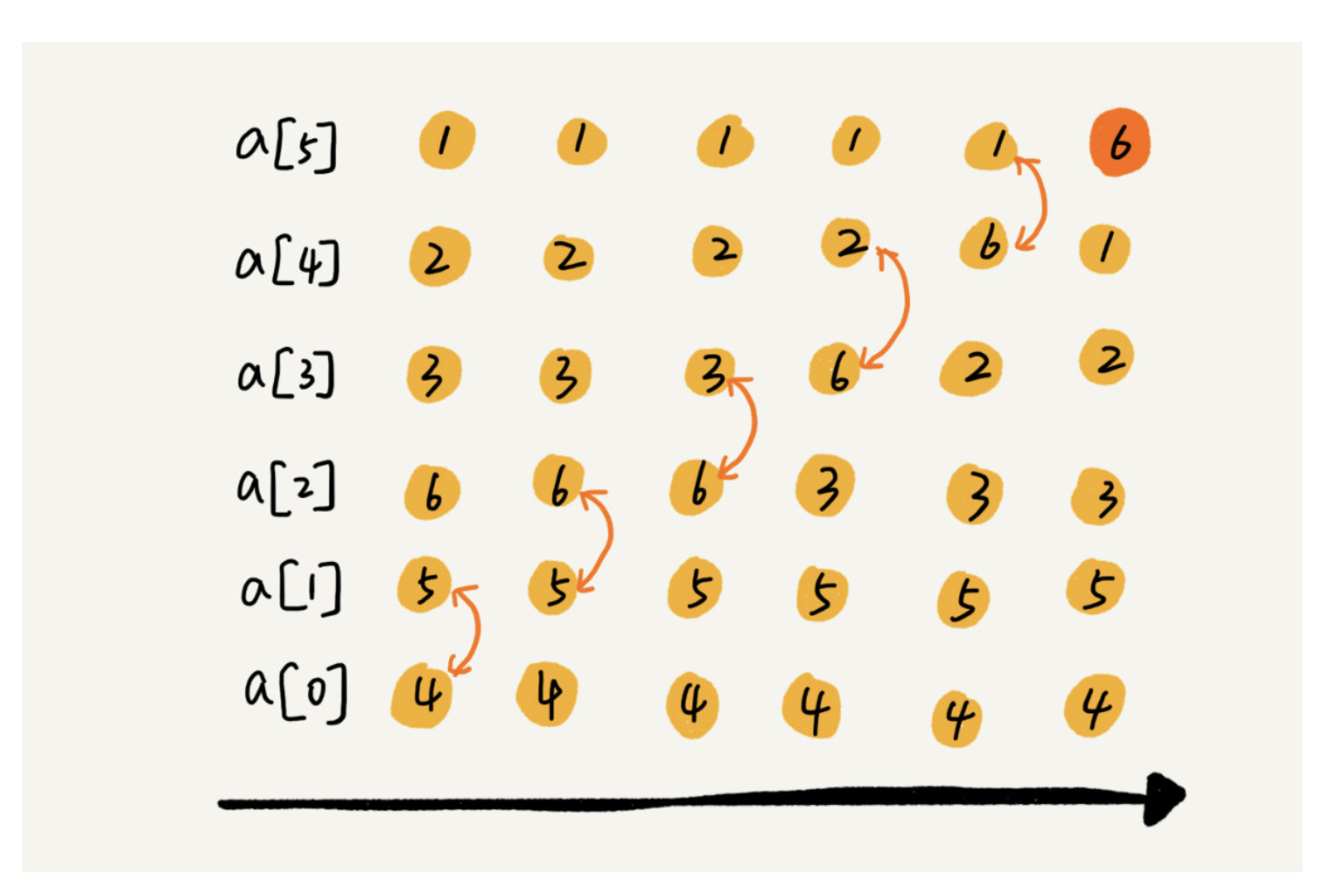
当某一次冒泡过程中未进行任何数据交换,则说明数据已经是有序的了,无需在进行循环。也就是说冒泡排序可以提前跳出循环的。
public static void bubbleSort(int[] array) {
if (array.length <= 1) {
return;
}
// 结束冒泡标识
boolean flag = false;
// 需要进行n次冒泡
for (int i = 0; i < array.length; i++) {
// 每次冒泡确定一个元素的位置。 所以第i次冒泡需要从 0比较到 length-i-1的地方
for (int j = 0; j < array.length - i - 1; j++) {
if (array[j] > array[j + 1]) {
int tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
flag = true;
}
}
if (!flag) {
return;
}
}
}
插入排序
将数组中的元素分为两个区间,已排序区间、未排序区间。初始的已排序区间只有一个元素,就是数组的第一个元素。插入排序的核心思想就是取未排序区间中元素,在已排序区间中找到合适的插入位置插入,并保证已排序区间一直有序。重复这个过程直到未排序区间元素个数为0,结束。
插入排序示意图

代码如下:
public void insertionSort(int[] a) {
// 初始:未排序区间 1 ~ n
for (int i = 1; i < a.length; i++) {
int j = i - 1;
int value = a[i];
// 取第i个元素在已排序区间找它的位置 已排序区间从后往前比较
for (; j >=0; j--) {
if (a[j] > value) {
a[j + 1] = a[j];
}else {
break;
}
}
a[j + 1] = value;
}
}
选择排序
选择排序的思想有点类似插入排序,也分为已排序区间,未排序区间,但是选择排序每次会从未排序区间选取最小的元素,将其放置到已排序区间末尾。
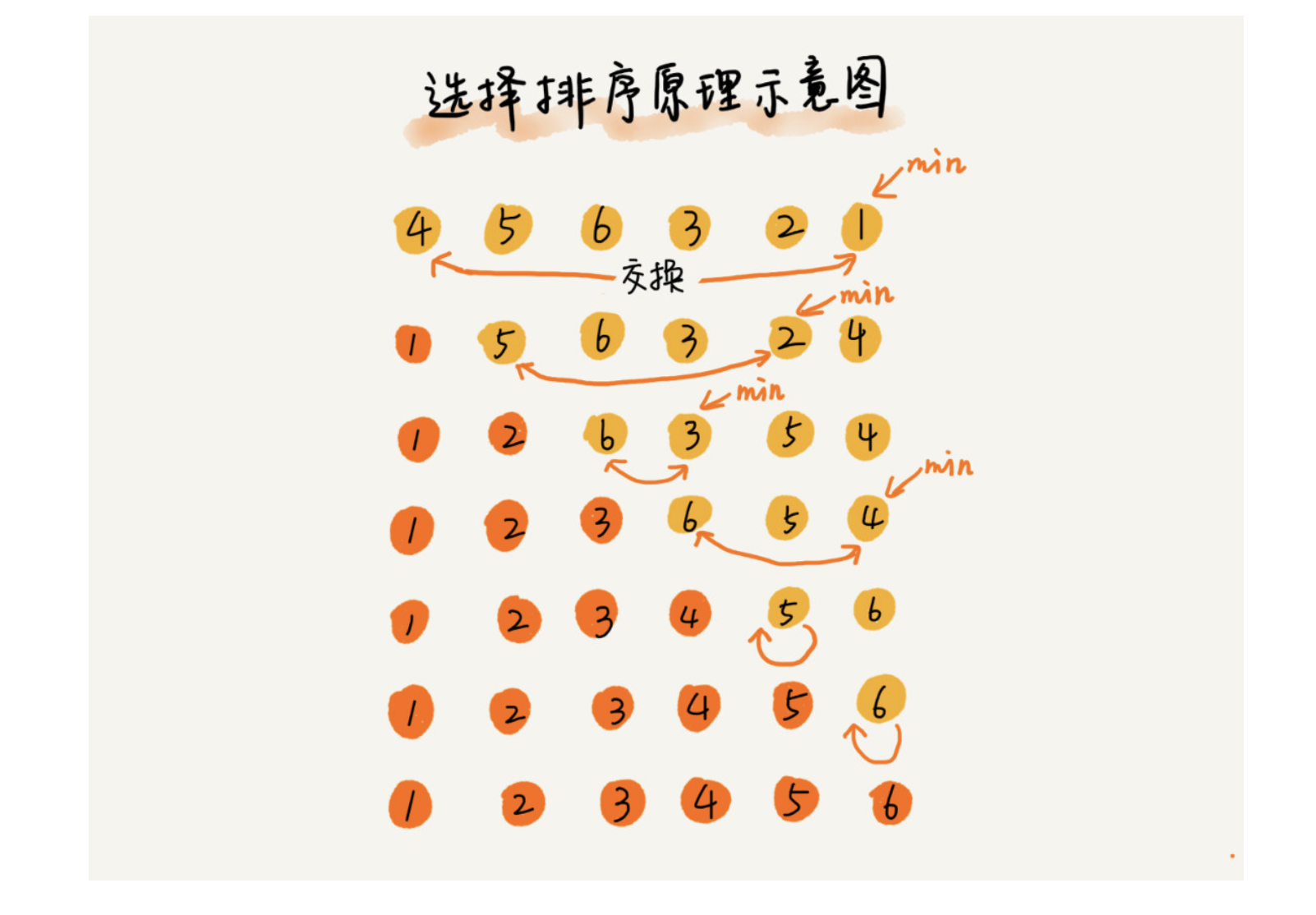
代码如下:
public void selectionSort(int[] a) {
// 每次选择一个 需要执行n次
for (int i = 0; i < a.length; i++) {
int j = i;
int minIndex = i;
// 从未排序数组中找出最小的
for (; j < a.length; j++) {
if (a[minIndex] > a[j]) {
minIndex = j;
}
}
//第i次操作就是要交换第i个元素 最小位置 和 a[i]交换
int value = a[i];
a[i] = a[minIndex] ;
a[minIndex] = value;
}
}
归并排序
归并排序的核心思想是,如果要排序一个数组,先把数组从中间分成两部分,分别对这两个部分排序,然后在合并起来就可以了。这就是分治思想。下面是归并排序的图解。
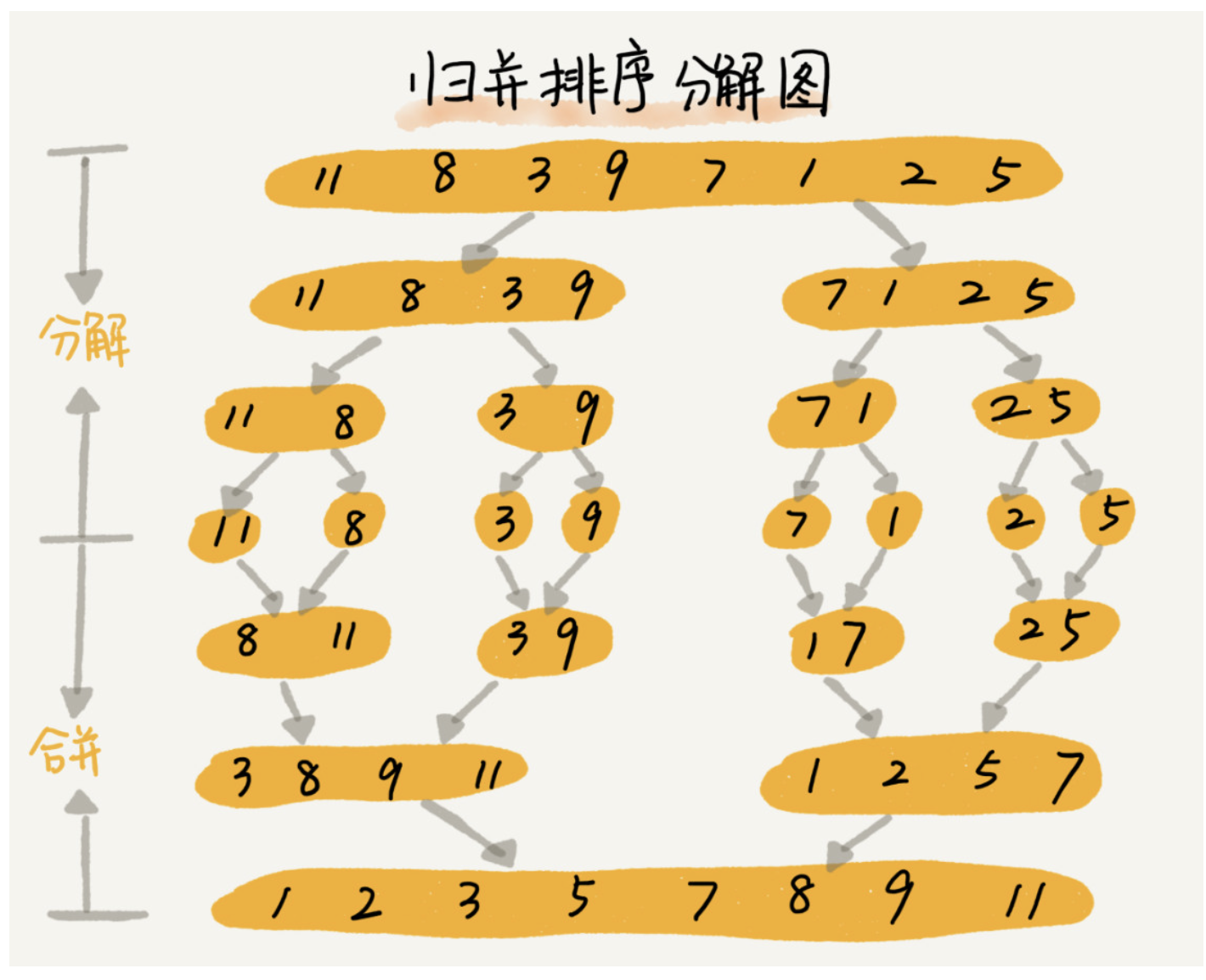
分治一般都是由递归实现,不难看出递推公式如下
递推公式:
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件:
p >= r 不用再继续分解
代码如下:
public void mergeSort(int[] a) {
int[] temp = new int[a.length];
sort(a, 0, a.length - 1, temp);
}
public void sort(int[] a, int start, int end, int[] result) {
if (start >= end) {
return;
}
int mid = (start + end) / 2;
sort(a, start, mid, result);
sort(a, mid + 1, end, result);
merge(a, start, mid, end, result);
}
public void merge(int[] a, int start, int mid, int end, int[] result) {
// 左边数起始位置
int leftStart = start;
// 右边数组起始位置
int rightStart = mid + 1;
// 结果数组下标
int resultIndex = start;
while (leftStart <= mid && rightStart <= end) {
if (a[leftStart] > a[rightStart]) {
result[resultIndex] = a[rightStart];
rightStart += 1;
} else {
result[resultIndex] = a[leftStart];
leftStart += 1;
}
resultIndex += 1;
}
while (leftStart <= mid) {
result[resultIndex] = a[leftStart];
leftStart += 1;
resultIndex += 1;
}
while (rightStart <= end) {
result[resultIndex] = a[rightStart];
rightStart += 1;
resultIndex += 1;
}
for (resultIndex = start; resultIndex <= end; resultIndex++) {
a[resultIndex] = result[resultIndex];
}
}
快速排序
快速排序的思想是,如果要对下标p到r的一个数组排序,我们选择p到r之间任意一点作为pivot(分界区)。遍历p到r,将大于pivot的放右边,小于pivot的放左边,pivot方中间。这样的话左边的数据全部都小于右边,在按照归并排序将左右两部分排序,直到区间减小为1,就说明整个数组都是有序的了
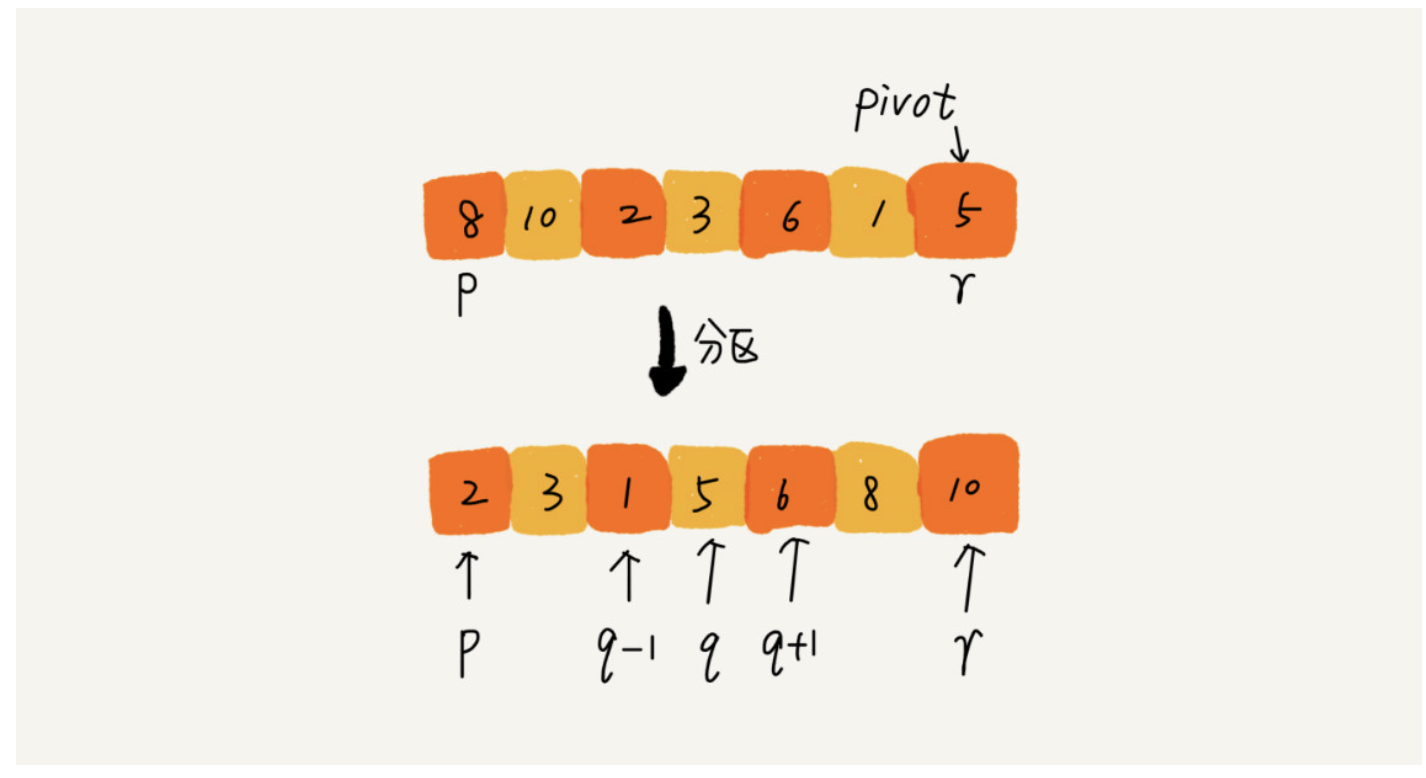
原地分区逻辑
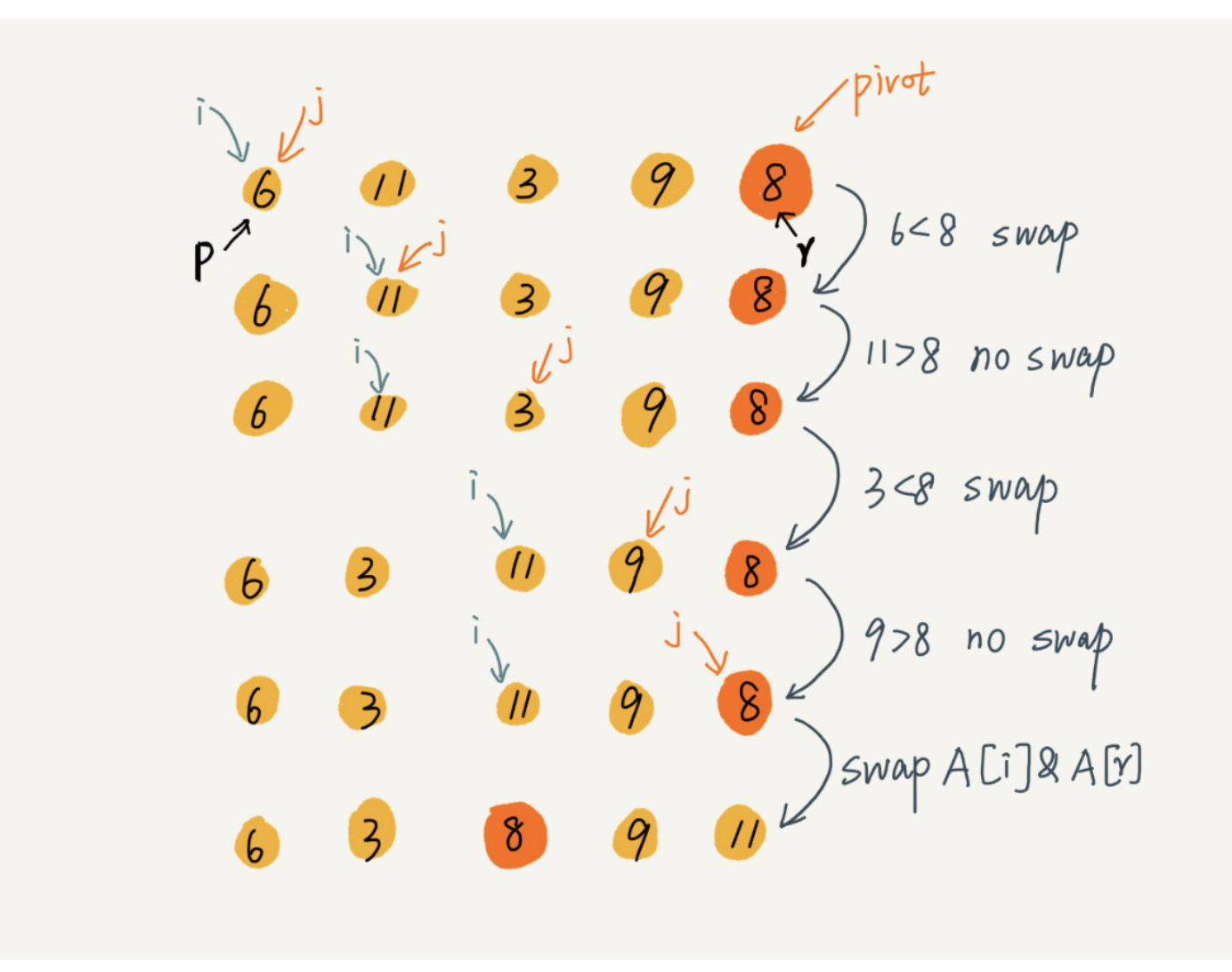
递推公式
递推公式:
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1, r)
终止条件:
p >= r
代码:
public void quickSort(int[] a) {
sort(a, 0, a.length - 1);
}
public void sort(int[] a, int start, int end) {
if (start >= end) {
return;
}
// 分区找到分界点的下标
int q = partition(a, start, end);
sort(a, start, q - 1);
sort(a, q + 1, end);
}
private int partition(int[] a, int start, int end) {
// 从start 到i 为已处理区间,即每次去一个数,跟pivot对比,若小于pivot,放入已处理区间
// i-1 代表已处理区最后元素的下标
int i = start;
int pivot = a[end];
for (int j = start; j < end ; j++) {
if (a[j] < pivot) {
// 小于,则需要把 a[j] 放在已处理区末尾就可以了 即a[i]
int tmp = a[j];
a[j] = a[i];
a[i] = tmp;
i += 1;
}
}
// 处理完了 交换a[i] 和 a[end]即 将pivot放到两个区域中间
a[end] = a[i];
a[i] = pivot;
return i;
}
复杂度
各种排序算法的时间复杂度、空间复杂度
| 排序算法 | 是否原地排序 | 是否稳定排序 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 |
|---|---|---|---|---|---|---|
| 冒泡排序 | 是 | 是 | O(1) | O(n2) | O(n2) | O(1) |
| 插入排序 | 是 | 是 | O(1) | O(n2) | O(n2) | O(1) |
| 选择排序 | 是 | 否 | O(n2) | O(n2) | O(n2) | O(1) |
| 归并排序 | 否 | 是 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) |
| 快速排序 | 是 | 否 | O(nlogn) | O(n2) | O(nlogn) | O(1) |