[数据结构与算法]数据结构与算法之图的深度优先遍历(DFS)

前要

树的先根遍历

学习图的深度优先遍历 (DFS)，先复习下 树的深度优先遍历(这里以先根遍历为例)。

//树的先根遍历
void PreOrder(TreeNode *R*){
	if(R!=NULL){
		visit(R); //访问根节点
		while(R还有下一个子树T){
			PreOrder(T);  //先根遍历下一颗子树
		}
	}
}

新找到的相邻接点一定是没有访问的。

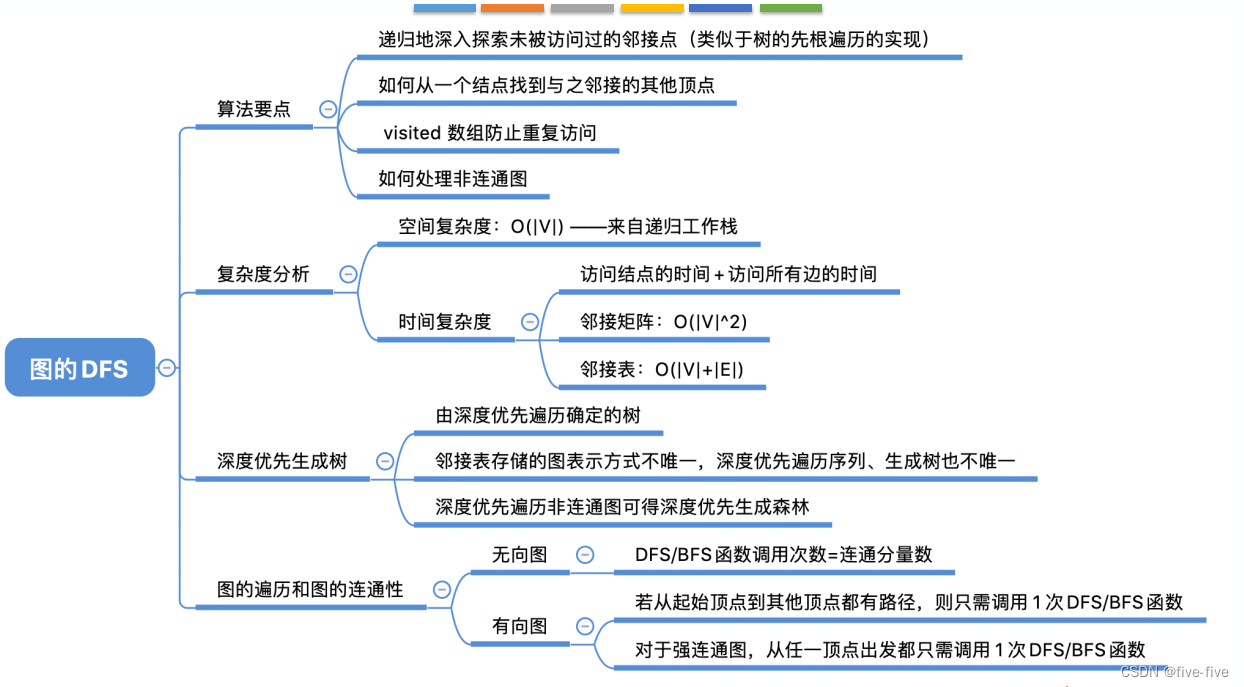
图的深度优先遍历

这里的 FirstNeighbor(G,v) 和 NextNeighbor(G,v,w) 同上文 方法说明

bool visited[MAX_VERTEX_NUM]; //访问标记数组
void DFS(Graph G,int v){  //访问标记数组
	visit(v); //从顶点v出发,深度优先遍历图G
	visited[]=TRUE;  //设已访问标记
	for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)){ 
			if(!visited[w]){  //w为u的尚未访问的邻接顶点
				DFS(G,w);
		}
	}
}

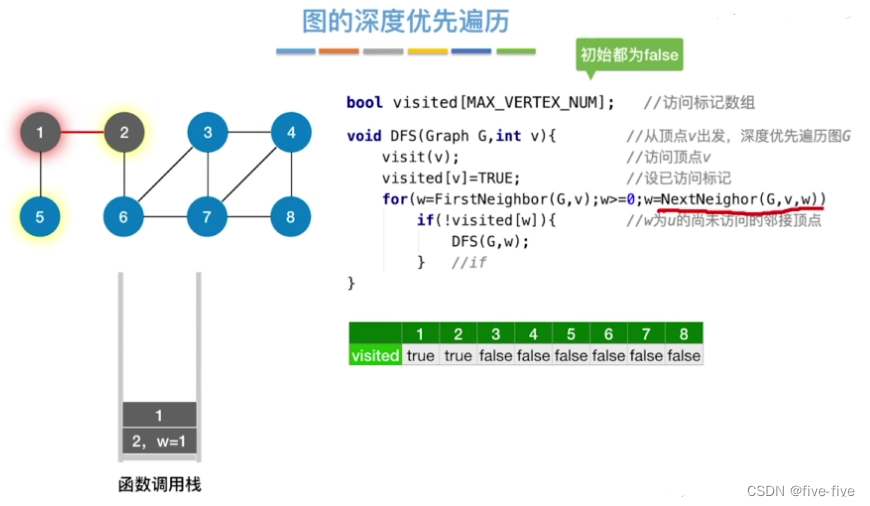
算法存在的问题

如果是非连通图，则无法遍历完所有结点

bool visited[MAX_VERTEX_NUM]; //访问标记数组

void DFSTrave(Graph G){
	for(v=0;v<G.vexnum;v++){
		visited[v]=FALSE;
	}
	for(v=0;v<G.vexnum;v++){
		if(!visited[i]){
			DFS(G,v);
		}
	}
}

void DFS(Graph G,int v){  //访问标记数组
	visit(v); //从顶点v出发,深度优先遍历图G
	visited[]=TRUE;  //设已访问标记
	for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)){ 
			if(!visited[w]){  //w为u的尚未访问的邻接顶点
				DFS(G,w);
		}
	}
}

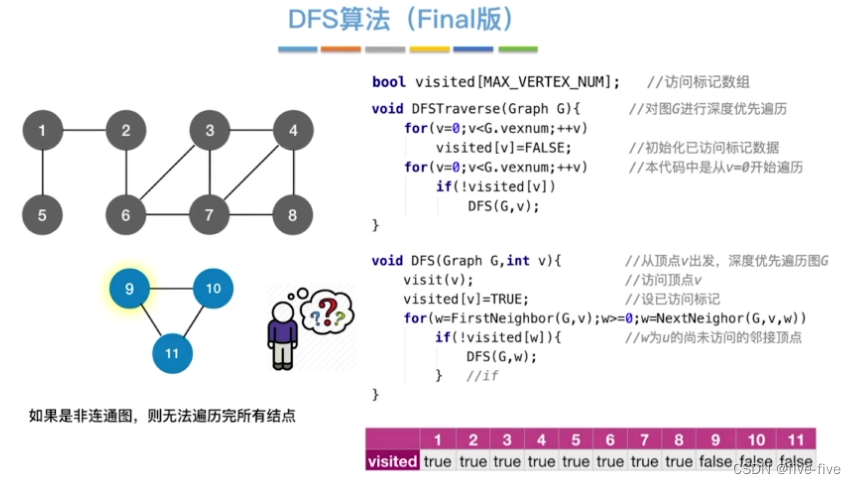
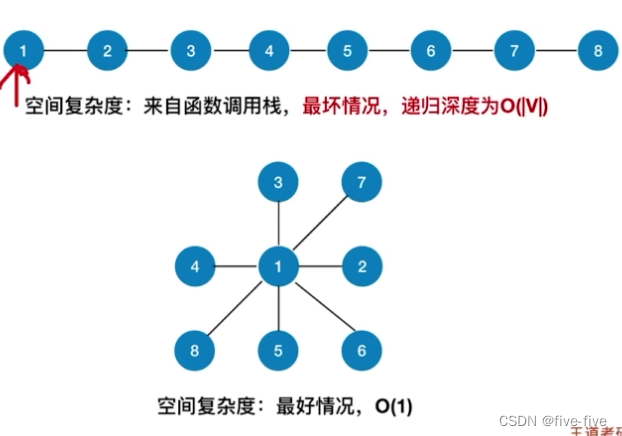
算法复杂度分析

时间复杂度=访问各节点所需时间 + 探索各条边所需时间

邻接矩阵

1. 访问 $|V|$个顶点需要 $O|V|$的时间
2. 查找每个顶点的邻接点都需要 $O(|V|)$的时间，而总共有|V|个结点，时间复杂度=$O(|V{|}^2)$

邻接表

1. 访问|V|个顶点需要 O(|V|) 的时间
2. 查找各个顶点的邻接点共需要 $O(|E|)$的时间，时间复杂度为：$O(|V|+|E|)$。

注意：

1. 同一个图的邻接矩阵表示方式唯一，因此深度优先遍历序列唯一
2. 同一个图的邻接表表示方式不唯一，因此深度优先遍历序列不唯一

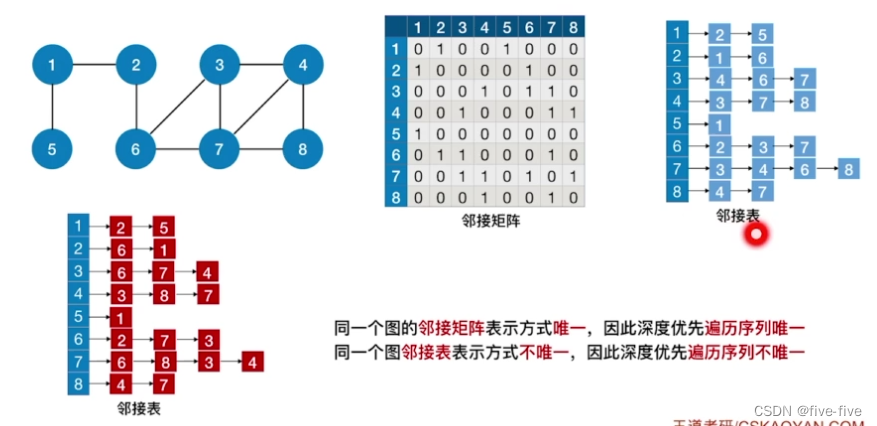
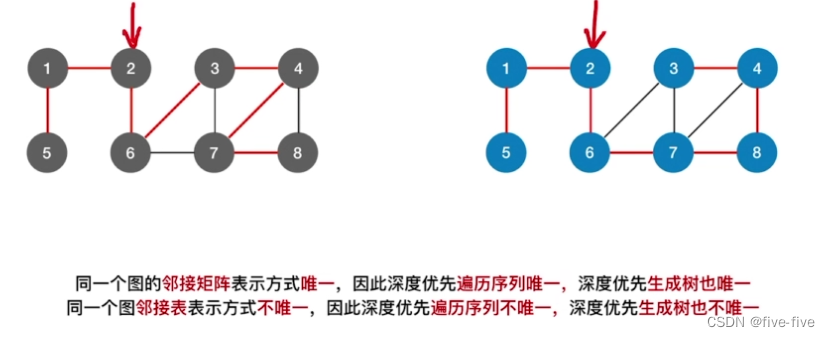
深度优先生成树

1. 同一个图的邻接矩阵表示方式唯一，因此深度优先遍历序列唯一，深度优先生成树也唯一
2. 同一个图的邻接表表示方式不唯一，因此深度优先遍历序列不唯一，深度优先生成也不唯一

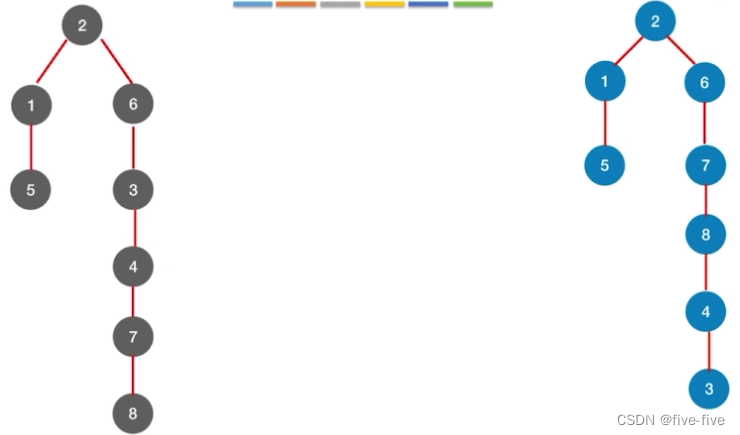
树节点示意图

生成树示意图

深度优先生成森林

同 广度优先生成森林 一样

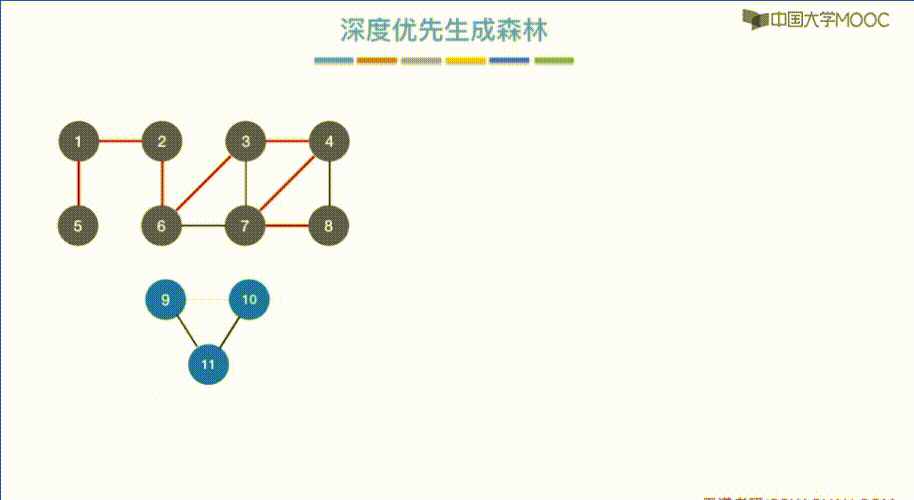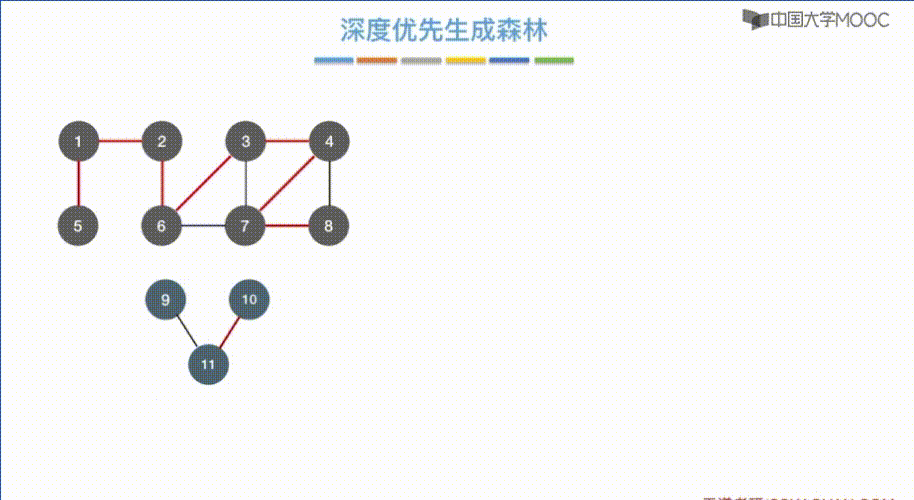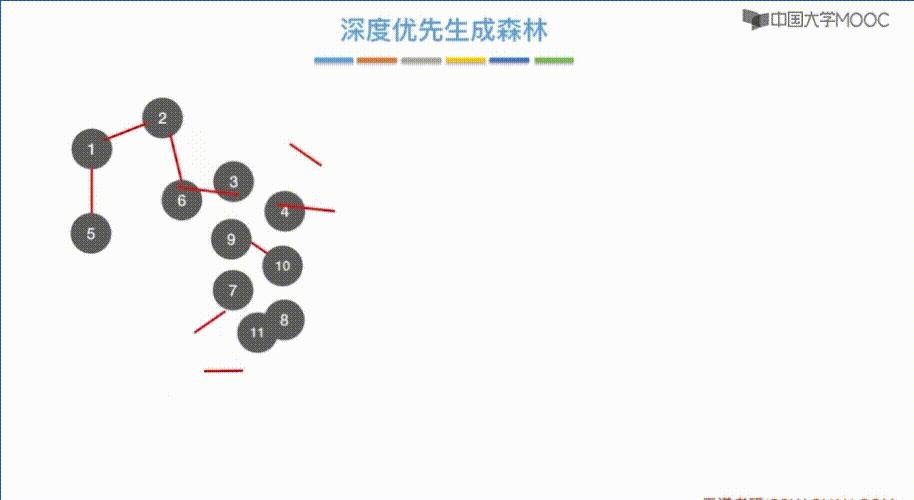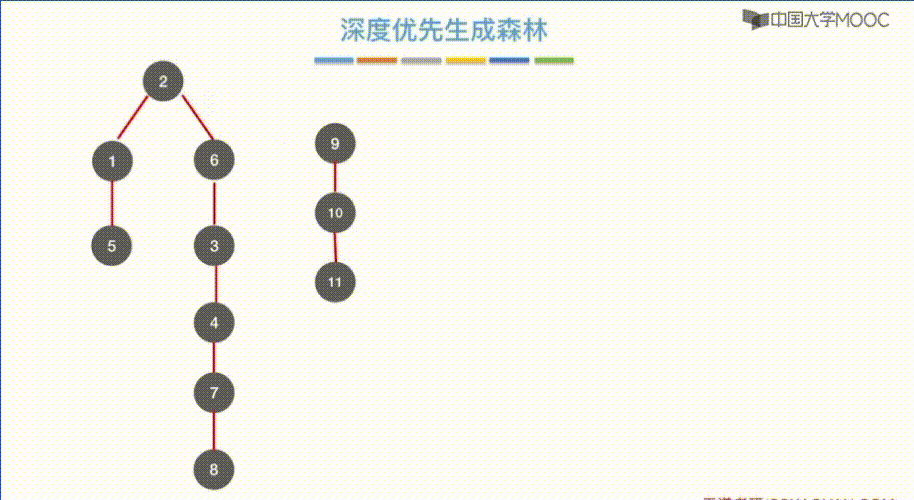
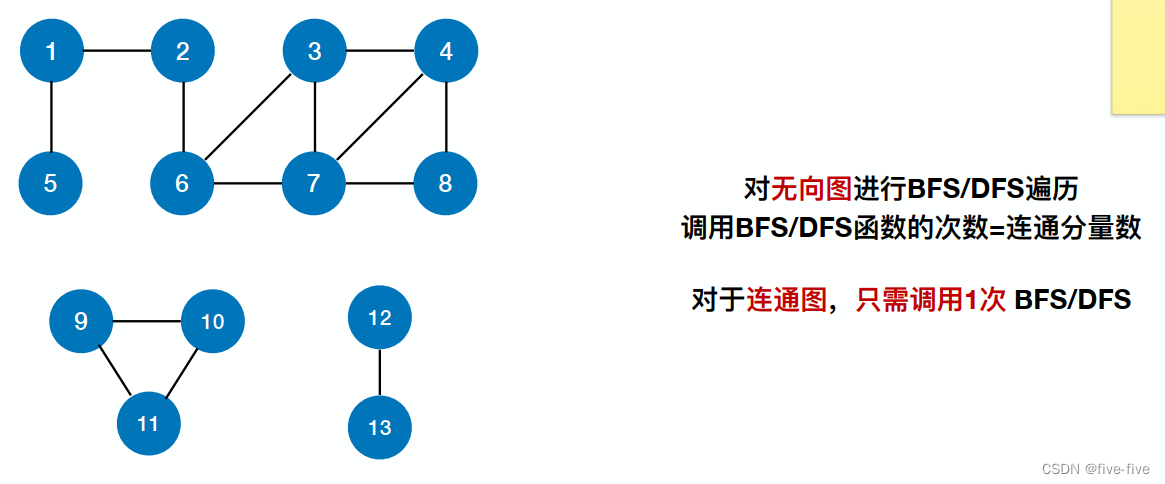
图的遍历与图的连通性

1. 对无向图进行 BFS/DFS 遍历，调用 BFS/DFS 次数=连通分量数
   1. 对于连通图，只需调用 1 次 BFS/DFS
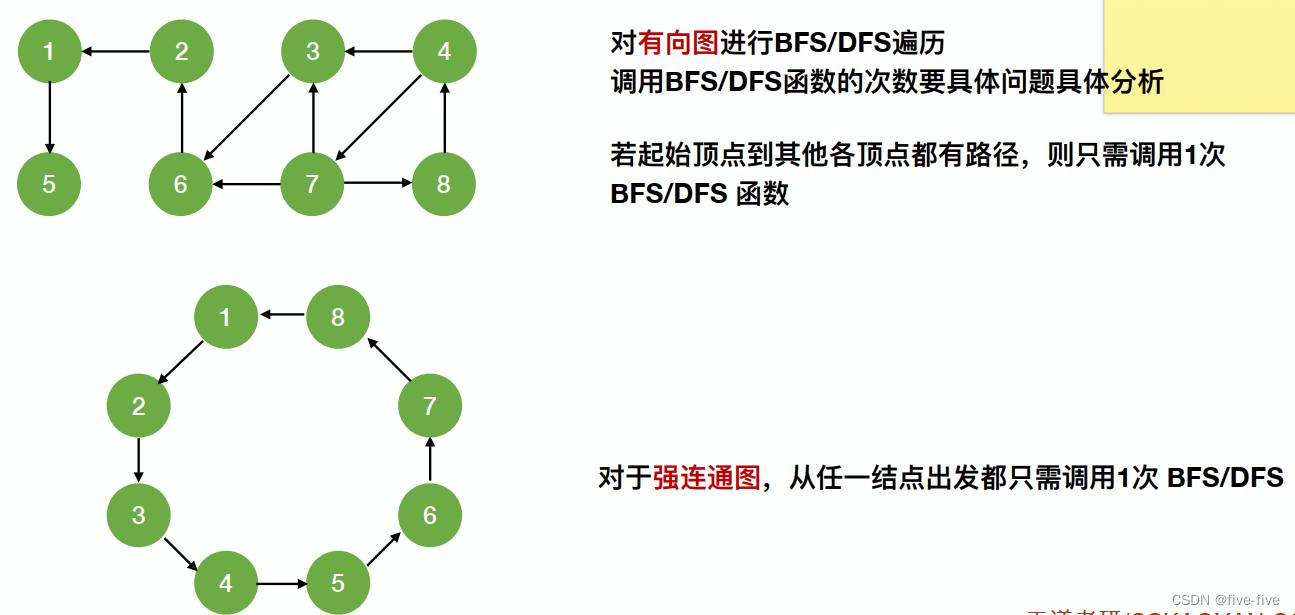
2. 对有向图进行 BFS/DFS 遍历，调用 BFS/DFS 次数要具体分析
   1. 若起始顶点到其他各顶点都有路径，则只需要调用 1 次 BFS/DFS 函数
3. 对于强连通图，从任一结点出发都只需要调用 1 次 BFS/DFS。
   无向图&连通图
   

有向图&强连通图

知识回顾与重要考点