Z 字形变换
算法标签:字符串、找规律


?
给出一个字符串,需要把它先按 Z 字行写一遍,然后再按行读出来,用数字来表示字符串,假设字符串里面的第一个字符是 0,第二个字符是 1,以此类推 . . . 题目给出了行数等于 4,按 Z 字形排列如下图所示

然后按照行输出,先输出第一行,再输出第二行 . . . 以此类推
行数是 4 表示第一列有 4 个数,行数是 7 表示第一列有 7 个数,这里都是行数大于 1 的情况,如果行数是 1,需要特判
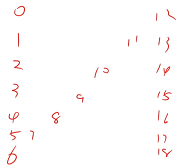
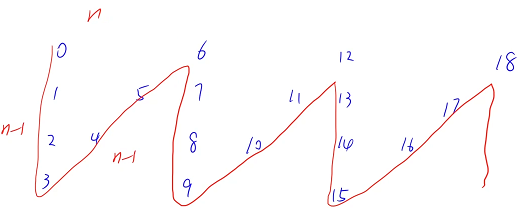
输出的时候按行来输出,先来看一下第一行输出的时候规律是什么
第一行是以 0 开头的,公差是 6 的等差数列,这个 6 是怎么来的呢?
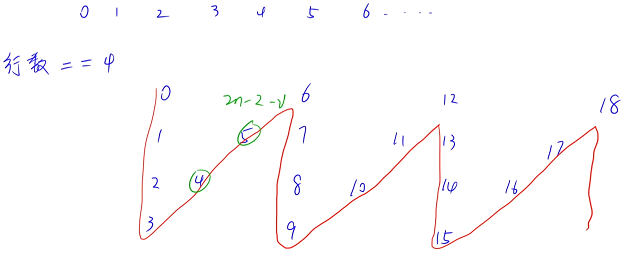
如果行数是 n,从第一个数开始,第一列除了第一个数之外有 n - 1 个数,斜边除了第一列的最后一个数之外有 n - 1 个数,所以从 0 → 6 要数 2n - 2 个数,所以公差是 2n - 2,第一行是以 0 开头的,公差是 2n - 2 的一个等差数列,最后一行是以 3 开头的,公差是
2n -? 2 的等差数列
接下来看一下除了第一行和最后一行之外的行,中间这些行我们可以把它拆成两个等差数列
把它拆成在竖线上的等差数列和在斜线上的等差数列
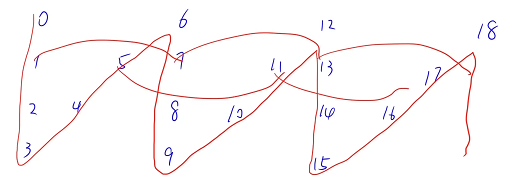
在竖线上的数也是一个公差为 2n - 2 的等差数列
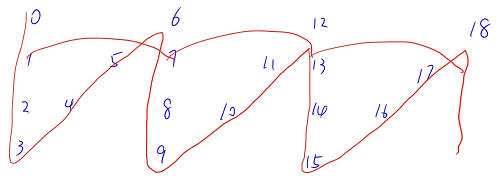
在斜线上的数也是一个公差为 2n - 2 的等差数列
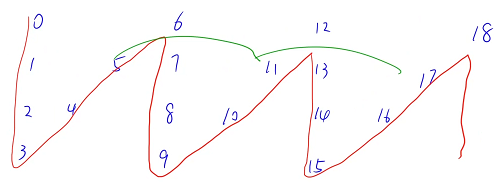
所以中间这些行其实是两个等差数列混在一块,先写第一个等差数列的一项,再写第二个等差数列的一项 . . . 以此类推
第一行和最后一行是一个等差数列,中间这些行是两个等差数列混合在一块(先写第一个等差数列的一项,再写第二个等差数列的一项),所有等差数列的公差都是 2n - 2,每个等差数列的起点是 0 ~ n - 1
接下来考虑斜线上的等差数列的起点是 5 和 4,这个 5 和 4 是怎么计算出来呢?
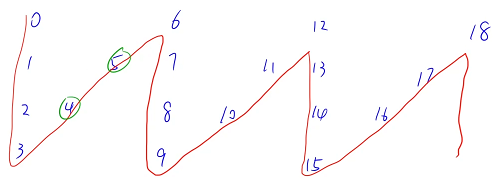
1 + 5 = 6
2 + 4 = 6
第一条斜线上的数与第一条竖线上的数之和是 2n - 2
所以斜线上的等差数列的首项 = 2n - 2 - 第一条竖线上的数
?
class Solution {
public:
string convert(string s, int numRows) {
//定义答案序列
string res;
//需要特判 n = 1 的情况还是原来的序列 当 n = 1 公差为 0 就会发生死循环 只要公差大于 1 都不会发生死循环
if(numRows == 1) return s;
//从第一行开始一直枚举到最后一行
for(int i = 0;i < numRows;i++) {
//如果是第一行或者是最后一行是一个首项是 i,公差是 2 × numRows - 2 的等差数列
if(i == 0 || i == numRows - 1) {
//j 从 i 开始
for(int j = i;j < s.size();j += 2 * numRows - 2)
res += s[j];
}
//如果是中间这些行是两个等差数列混在一起
else {
//每一行的第一个等差数列的首项是 i,第二个等差数列的首项是 2 * numRows - 2 - i
for(int j = i,k = 2 * numRows - 2 - i;j < s.size() || k < s.size();j += 2 * numRows - 2,k += 2 * numRows - 2) {
//先加第一个序列的再加第二个序列的
if(j < s.size()) res += s[j];
if(k < s.size()) res += s[k];
}
}
}
return res;
}
};整数反转
算法标签:数学
?
?
给出一个 32 位的有符号整数 x ,需要将这个整数的每一位上的数字进行反转后输出,如果翻转之后这个数溢出的话就返回 0
假设环境不允许存储 64 位整数(有符号或无符号)
尽量不要定义 long long 变量,只用 int 存储,然后特判会不会溢出就可以了
模拟样例
如果输入 123,输出 321,如果输入 -123,负号不需要考虑,输出 -321
法一
可以用 to_string( ) 转换成字符串,再用 reverse( ) 翻转,最后用 aoti( ) 转换成整数
法二
怎么把一个数的每一位拿出来?
以正数为例
①从个数开始拿,x % 10 就可以把 x 的个位数字取出来,让 x? / 10 就可以把 x 的个位数字删掉,最后输出 4 3 2 1

②再把 4、3、2、1 变成一个整数,先定义一个变量 r = 0,从最高位开始加
r = r × 10 + 最高位数字 最后就可以把这个数变成一个整数

把两步合在一块,先定义一个 r 等于 0,每一次的个位就是要加的最高位
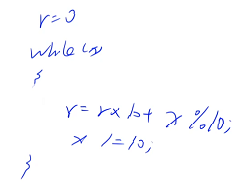
为了方便,先用 long long 存储,最后再把 long long 换成 int
利用 c++ 中取模运算的性质,一个正数模上一个数得到的是正数,一个负数模上一个数得到的是负数
数学上的取模运算,余数一定是大于等于 0 的
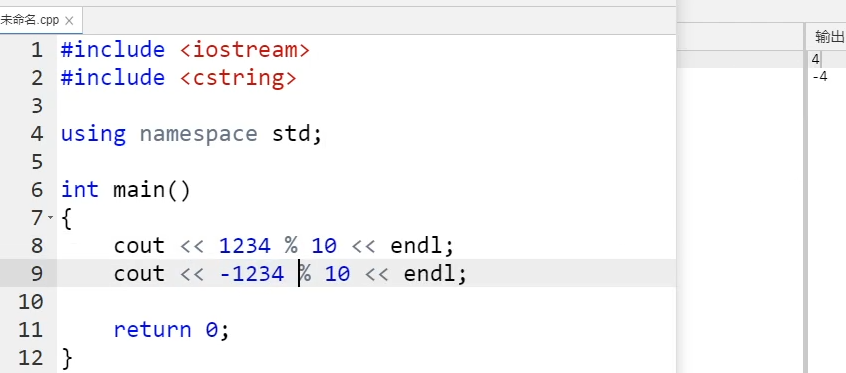
所以刚才的分析对于负数同样适用
?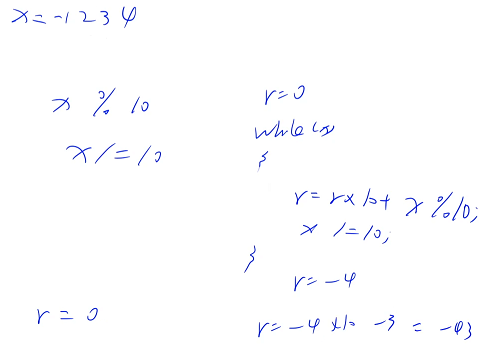

数学取模的含义:两个数的差值应该是 10 的整数倍,6 - ( - 4 ) 才是 10 的整数倍
class Solution {
public:
int reverse(int x) {
long long r = 0;
while(x) {
r = r * 10 + x % 10;
x /= 10;
}
//r 大于 int 的最大值
if(r > INT_MAX) return 0;
if(r < INT_MIN) return 0;
return r;
}
};由于题目规定了不能使用 long long 存储 🤡,接下来考虑一下更严谨的做法
如果把?r?改成?int 其实就是看一下 r?=?r?*?10?+?x?%?10;这行代码什么时候会溢出,有两种情况:r?是正数,r 是负数
r 为正数什么时候溢出呢?
用 max 减去左边的数来计算就不会溢出了,判断溢出只需要判断以下式子是否成立就可以了
r 为负数什么时候溢出呢?
两个负数相加可能小于 INT_MIN
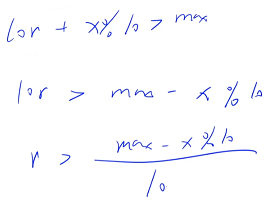
?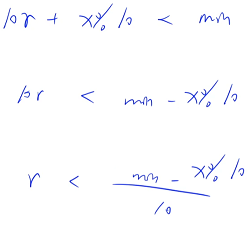
class Solution {
public:
int reverse(int x) {
int r = 0;
while(x) {
//如果溢出返回 0
if(r > 0 && r > (INT_MAX - x % 10) / 10) return 0;
if(r < 0 && r < (INT_MIN - x % 10) / 10) return 0;
//如果把 r 改成 int 就是看下面这行代码什么时候会溢出,有两种情况:r 是正数 r是负数
r = r * 10 + x % 10;
x /= 10;
}
return r;
}
};字符串转换整数 (atoi)
算法标签:字符串

?

?
要求实现一个 atoi 函数,把字符串转换成整数
规则如下
输入字符串开头可能会有一些空格,前面的空格直接删掉
如果第一个不是空格字符是正号或者负号的话就表示后面这个数的符号,如果两者都不存在,则假定结果为正。如果第一个非空的字符是数字,则从这个字符开始,后面连续的一段数字就是我们要转换的数
这个数的后面可能会有一些额外的字符,这些字符直接忽略就可以了
如果输入第一个非空格字符不是一个数就是非法输入直接输出 0
只要是无效输入就输出 0
如果存储的数大小范围不在 int 范围内也返回 0
①首先最一开始需要把前面所有空格都删掉了
res 存储的是正数,先把符号拿出来,然后存储它的绝对值
class Solution {
public:
int myAtoi(string str) {
//过滤字符串前面的所有空白字符
int k = 0;
while(k < str.size() && str[k] == ' ') k++;
//如果这个字符串已经过滤完了 整个字符串都是空格的话返回 0
if(k == str.size()) return 0;
//第一个字符可能是 '+' 或者 '-',定义符号默认是 '+'
int minus = 1;
//如果第一个字符是 '-',说明是一个负数,minus = -1,k 往后走一位
if(str[k] == '-') minus = -1,k++;
//否则如果第一个字符是 '+',说明是一个正数,k 往后走一位
else if(str[k] == '+') k++;
//定义答案,先用 long long 存储,之后再把 long long 改成 int
long long res = 0;
//k 是数字
while(k < str.size() && str[k] >= '0' && str[k] <= '9') {
res = res * 10 + str[k] - '0';
//k 往后移动一位
k ++;
//res 存储的是一个正数
if(res > INT_MAX) break;
}
//乘上原来的符号
res *= minus;
//如果大于最大值就输出最大值
if(res > INT_MAX) res = INT_MAX;
//如果小于最小值就输出最小值
if(res < INT_MIN) res = INT_MIN;
return res;
}
};由于题目规定了不能使用 long long 存储🤡,下面考虑一下更严谨的做法?
主要是判断这句话 res?=?res?*?10?+?str[k]?-?'0';有没有溢出
特判的时候也需要分成正数和负数两种情况判断

常量INT_MAX和INT_MIN_永不为辅的博客-CSDN博客
INT_MAX = 2^32 - 1 =?? 2147483647
INT_MIN? = -2^32?? ? = - 2147483648
负无穷的绝对值要比正无穷的绝对值多 1,如果 res 恰好是 - 2147483648,正数存储不下来,需要特判负无穷这个数,否则会溢出
class Solution {
public:
int myAtoi(string str) {
//过滤字符串前面的所有空格
int k = 0;
while(k < str.size() && str[k] == ' ') k++;
//字符串都被过滤完了 整个字符串都是空格返回 0
if(k == str.size()) return 0;
//第一个字符可能是 '+' 或者 '-',定义符号默认是 '+'
int minus = 1;
//如果第一个字符是 '-',说明是一个负数,minus = -1,k 往后走一位
if(str[k] == '-') minus = -1,k++;
//否则如果第一个字符是 '+',说明是一个正数,k 往后走一位
else if(str[k] == '+') k++;
//先用 long long 存储之后再把 long long 改成 int
int res = 0;
//k 是数字
while(k < str.size() && str[k] >= '0' && str[k] <= '9') {
int x = str[k] - '0';
//如果是正数并且溢出 直接返回最大值
if(minus > 0 && res > (INT_MAX - x) / 10) return INT_MAX;
//如果是负数也是一样的
if(minus < 0 && -res < (INT_MIN + x) / 10) return INT_MIN;
//特判溢出
if(-res * 10 - x == INT_MIN) return INT_MIN;
res = res * 10 + x;
//k 往后移动一位
k ++;
}
//乘上原来的符号
res *= minus;
//正无穷与负无穷的输出都在这里
return res;
}
};回文数
算法标签:数学

?
题目要求判断一个整数是不是回文数
回文数从左到右读和从右到左读是一样的,如果一个字符串翻转之后还是和原来一样的话也是回文数
特判:负数一定不是回文数,-121 翻转后是 121-????????????????
把它转换成一个字符串,(利用反向迭代器)把这个字符串翻转一遍看是否和原来字符串一样
class Solution {
public:
bool isPalindrome(int x) {
//特判负数
if(x < 0) return 0;
string s = to_string(x);
//初始化一个倒序的字符串
return s == string(s.rbegin(),s.rend());
}
};由于这道题目没有 long long 的限制,所以可以使用第 7 题的做法😪
class Solution {
public:
bool isPalindrome(int x) {
//特判负数
if(x < 0) return 0;
//由于 x 的值发生了改变 需要先存储 x
int y = x;
//从个位开始把 x 的每一位拿出来
long long res = 0;
//x 的个位就是 res 的首位
while(x) {
res = res * 10 + x % 10;
x /= 10;
}
return res == y;
}
};正则表达式匹配
算法标签:递归、字符串、动态规划
闫氏DP分析法 --- 01背包、完全背包_小雪菜本菜的博客-CSDN博客
闫氏DP分析法 --- 石子合并、最大上升子序列_小雪菜本菜的博客-CSDN博客
?
?
给出一个字符串 s 和一个字符串 p,要求实现一个正则表达式匹配的一个函数
s 当中不包含匹配符号,p 里面包含两种正则表达式的匹配符号
.? 可以匹配任意一种字符
*? 表示 * 前面那个字符可以出现 0 次、1 次、2 次、任意多次
.* 可以匹配任意一个字符串,字符串的长度是多少就给多少个 " . ",每个 " . " 可以匹配任意多个字符
模拟样例
aa 和 a 一定不匹配,这里面没有任何的匹配字符
![]()
aa 和 a* 是匹配的,因为 * 可以表示前面 a 出现 2 次
ab 和 .* 是匹配的,.* 可以匹配任意多个字符
aab 和 c*a*b 是匹配的,第一个 * 表示 c 出现 0 次,第二个 * 表示 a 出现 2 次,就可以匹配 aab 了
dp 问题的时间复杂度由 O( n^3 ) 最终优化为 O( n^2 )
如果按照定义来做,要把每一种匹配的方案都暴搜一遍(每个 * 表示多少个字符),但是所有匹配的方案数量应该是指数级别,为什么可以用 dp?由于 dp 每个状态可以表示一类方案
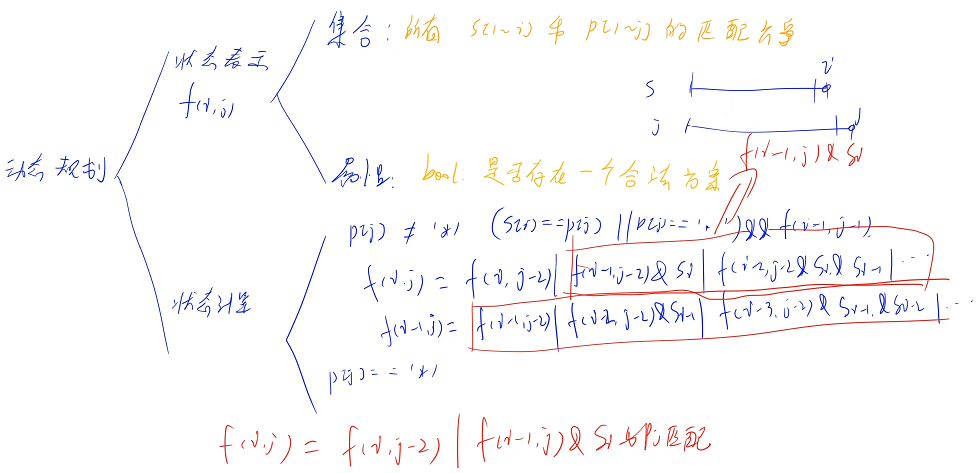
[ 状态表示 ] 一般两个字符串的问题用两维来表示
把每一个方案看成一个集合,看 f[ i ][ j ] 表示的是哪个集合
[ 状态计算 ] 接下来所有的分析,包括边界的分析,包括状态转移方程的分析都是围绕定义来看
题目问所有的匹配方式里面有没有匹配的一种情况,匹配方式有很多种,主要取决于 1 -? j? 里面每个 * 匹配几个字符,每个 * 可以匹配任意多个字符,因此有很多种匹配方式,需要在所有的方案中找一个合法的方案

问所有匹配方式中有没有匹配的一种情况
下标从 1 开始
首先看一下它是不是 ?*,需要把它看成一个整体
![]()
如果 p[ j ] ≠ ' * ',看 s[ i ] 和 p[ j ] 是不是匹配的,有两种情况,第一种情况:s[ i ] = p[ j ]。第二种情况:p[ j ] 可能是 ' . ',同时还要满足 s[ i - 1 ] 个字符与 p[ j - 1 ] 个字符是匹配的,整个才可以匹配
如果 p[ j ] = ' * ',就要枚举一下这个 ' * ' 表示多少个字符:' * ' 表示取 0 个字符、取 1 个字符、取 2 个字符 . . .
如果 ' * ' 表示 0 个字符,说明 ' ?* ' 是多余的

状态数量 n^2,转移数量需要枚举一遍是 O( n ),整个时间复杂度为 O( n^3 )
优化后时间复杂度由 O( n^3 ) 变成 O( n^2 )
& si 表示 s[ i ] 和 p[ j ] 是不是匹配,最终的状态转移方程是 O( 1 )
如果 s 串一个字符都没有,可能是和 p 串匹配的,因为 p 串里面可能有 ' * ',' a* ' 也可以表示空字符串
第一个字符串为 0,第二个字符串不为 0 是可以存在的
如果第二个字符串从 0 开始,首先 f[ 0 ][ 0 ] 已经初始化过了,如果是 f[ 1 ][ 0 ],一定是不匹配的,一个非空的串是不可能匹配一个空串的,所以 j 从 0 开始没有意义,j 从 1 开始就可以了
class Solution {
public:
bool isMatch(string s, string p) {
//用 n 和 m 表示两个字符串的长度
int n = s.size(),m = p.size();
//让两个字符串的下标从 1 开始
s = ' ' + s,p = ' ' + p;
//定义状态转移方程,下标从 0 - n,一共 n + 1 个数
vector<vector<bool>> f(n + 1,vector<bool>(m + 1));
//第一个串和第二个串都是空串的时候是匹配的
f[0][0] = true;
//枚举所有状态 第一个串从 0 开始到 n
for(int i = 0;i <= n;i++)
//考虑第二个串要不要从 0 开始呢?
for(int j = 1;j <= m;j++) {
//需要把 'a*' 看成一个整体 如果满足条件,当前的字符不能单独使用,可以直接 continue
if(j + 1 <= m && p[j + 1] == '*') continue;
/* 第一种情况 i 有可能从 0 开始
由于字符串下标从 1 开始,i 从 0 开始没有意义 不表示任意字符
避免越界
*/
if(i && p[j] != '*') {
f[i][j] = f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.');
}else if(p[j] == '*') {
//注意 si 和 pj 匹配其实是 si 和 pj-1 匹配 因为 pj 是 '*' pj-1 才是它前面的字符
f[i][j] = f[i][j - 2] || i && f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '.');
}
}
//判断 f[n][m] 是不是 true
return f[n][m];
}
};