1. 概念:什么是递归?
递归(Recursion)是一种解决问题的方法。尤其是复杂问题,有时用递归解决复杂问题可能会出奇的简单。
递归将一个比较复杂的问题分解成更小规模的问题,持续分解直到问题规模小到可以用非常简单的方式直接解决。
分解在算法上的表现出来的就是:在算法流程中调用自身。
2. 举例说明递归:数列求和
问题:给定一个列表,返回所有数的和,列表中数的个数不定。
2.1 用循环的解法:
需要一个循环和一个累加变量来迭代求和。
def sum_list(alist):
sum_of_list = 0
for i in alist:
sum_of_list = sum_of_list + i
return sum_of_list
print(sum_list([1, 3, 5, 7, 9]))
2.2 如果不使用while或for的话,还能求解吗?
数列求和,其实是由很多次的两个数相加实现的。我们需要做的,是如何将规模大的数列求和分解为规模小的两数求和。同样属于求和问题,只是规模发生了变化,这就是递归解决问题的特征。
对[1, 3, 5, 7, 9]这个数列进行求和,除了循环,还有另外一种方式:全括号表达式(1 + (3 + (5 + (7 + 9))))
最内层的 (7 + 9) 直接相加就可以计算的出。
然后 (5 + (7 + 9)) 就可以用 (5 + 16) 直接计算出。
整个求和的过程就是:
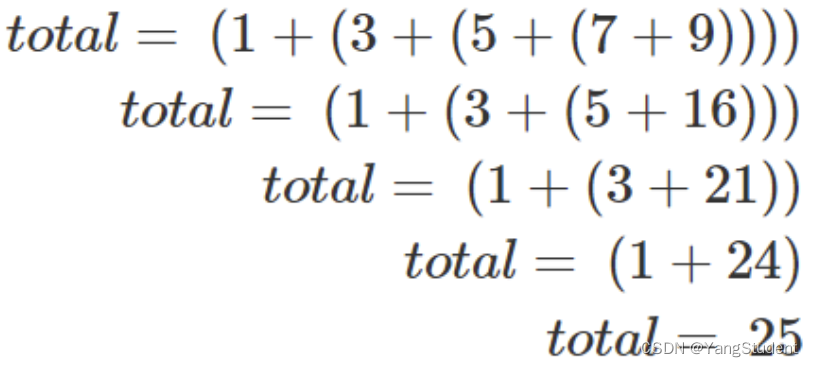
s u m _ l i s t ( a l i s t ) = a l i s t [ 0 ] + s u m _ l i s t ( a l i s t [ 1 : ] ) sum\_list(alist) = alist[0] + sum \_ list(alist[1: ]) sum_list(alist)=alist[0]+sum_list(alist[1:])
写成代码就是:
def sum_list(alist):
# 问题的最小规模,直接输出
if len(alist) == 1:
return alist[0]
else:
# 调用函数自身,减小函数的规模
return alist[0] + sum_list(alist[1:])
print(sum_list([1, 3, 5, 7, 9]))
这个程序的重点在于:
- 给出了最小规模的条件,可以直接解决最小问题。
- 具备分解问题的步骤,通过调用函数自身减小问题的规模。
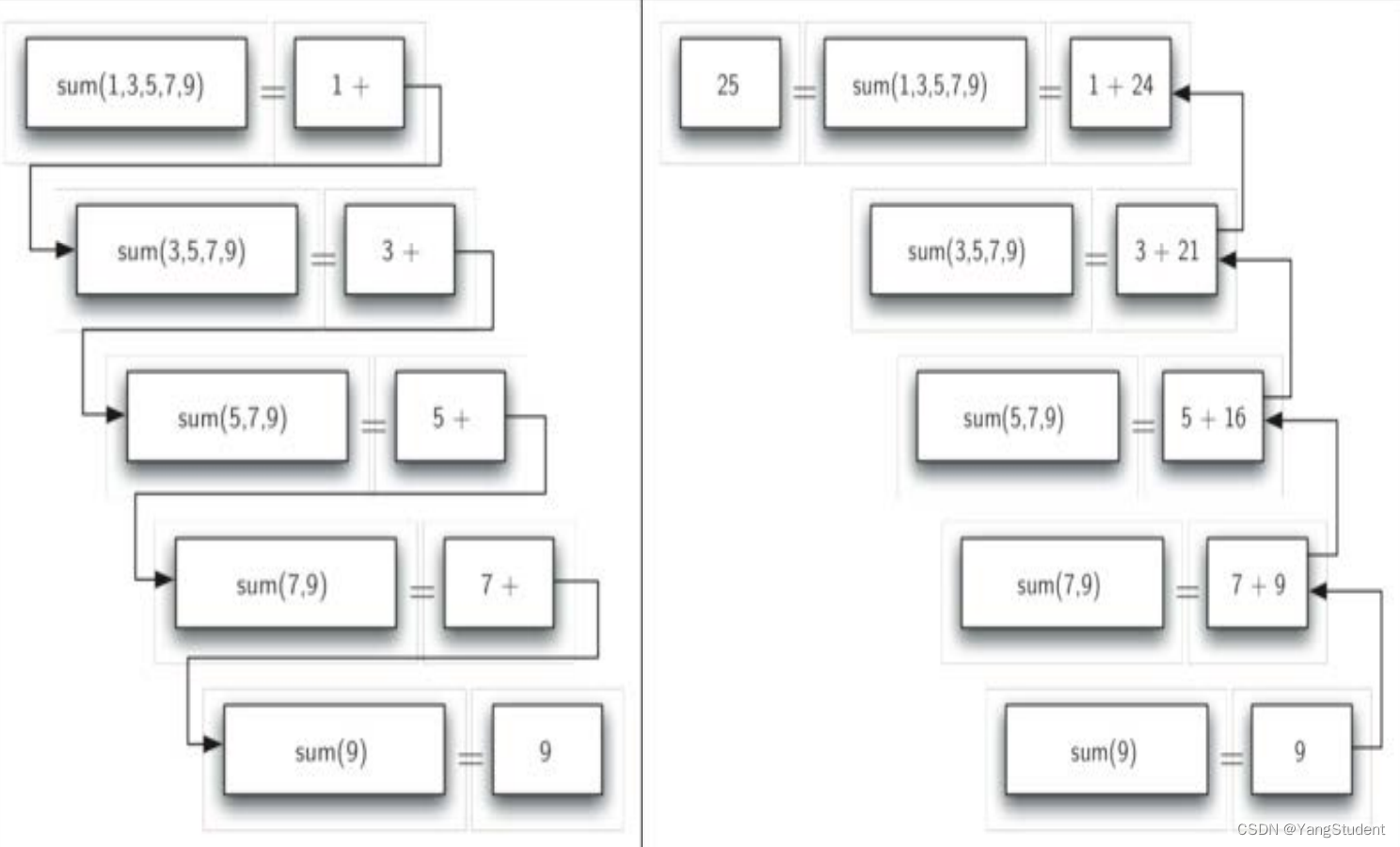
函数的执行和返回过程如下图。
2.3 递归三定律
1,递归算法必须有一个基本结束条件(最小规模问题的直接解决)
2,递归算法必须能改变状态向基本结束条件演进(减小问题规模)
3,递归算法必须调用自身(解决减小了规模的相同问题)
对于上例的数列求和问题,对应的三定律分别为:
1,数列求和问题首先具备了基本结束条件:当列表长度为1的时候,直接输出所包含的唯一数
2,数列求和处理的数据对象是一个列表,而基本结束条件是长度为1的列表,那递归算法就要改变列表并向长度为1的状态演进。我们看到其具体做法是将列表长度减少1
3,调用自身是递归算法中最难理解的部分,实际上我们理解为“问题分解成了规模更小的相同问题”就可以了在数列求和算法中就是“更短数列的求和问题
2.4 简易高效理解
如果你还没懂的话,问题不大,因为我看完了也是懵的。
对于递归有没有什么好的理解方法? - 方应杭的回答 - 知乎
https://www.zhihu.com/question/31412436/answer/738989709
这篇文章能更帮助理解。
3. 递归的应用
3.1 十进制整数转换为任意进制
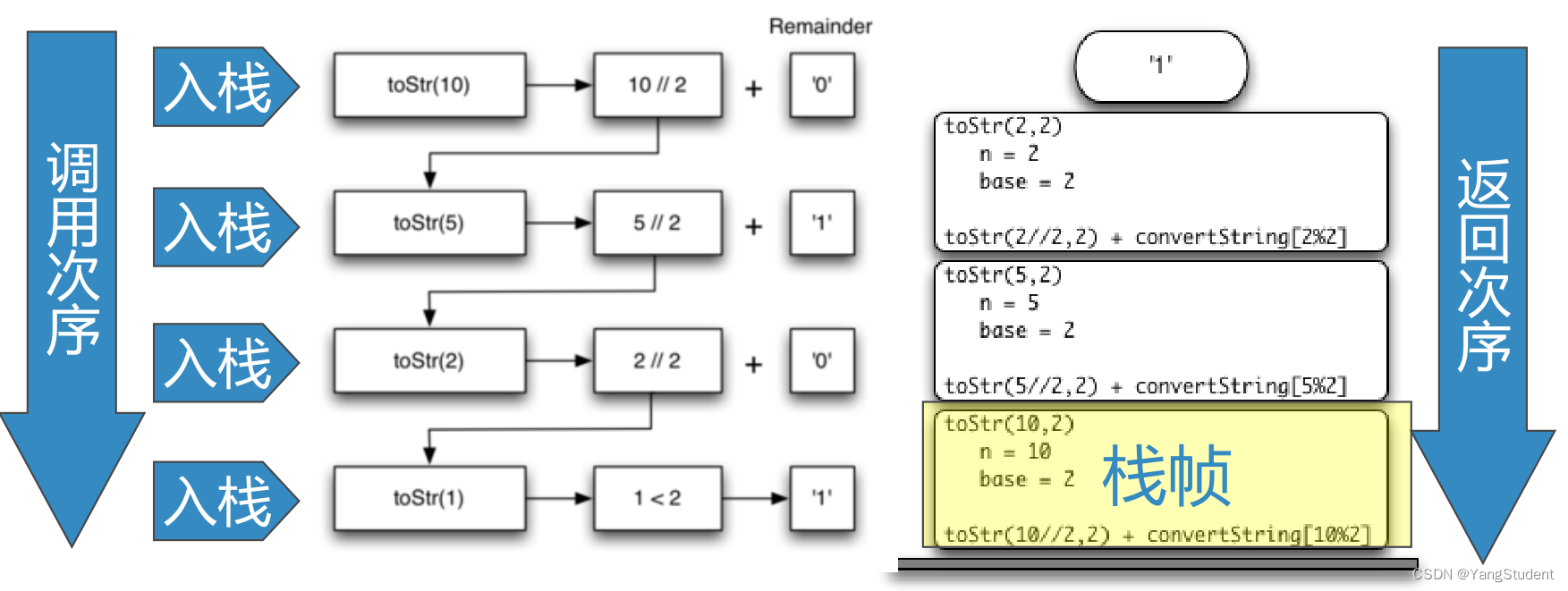
之前曾用栈实现过进制的转换,这里,采用递归实现。递归和栈具有一定的关系。递归要解决的是从十进制到二进制、四进制、八进制、十六进制等进制的任意进制转换。
首先来看最熟悉的十进制,即十进制整数转换为十进制。
十进制包含10个符号:conv_string = “0123456789”
对于小于10的十进制整数,如“5”,直接查表就行了
conv_string[5]
因此本题的基本结束条件就是一位的整数小于基(即进制数,十进制的基就是10,十六进制的基就是16),直接查表并输出。
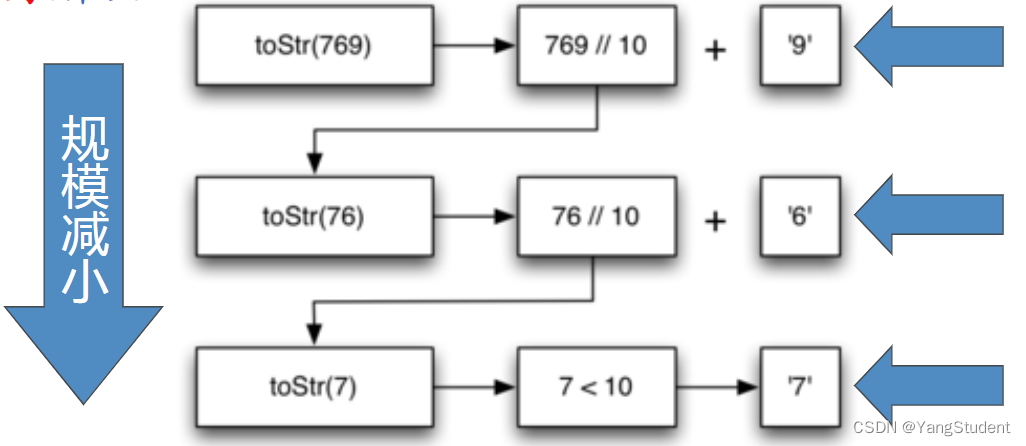
对于大于10的十进制整数,如“769”,延续上面的方法,把“769”拆分成多个小于“10”的整数就行了,即拆分成 “7” , “6”, “9”,然后将这个三个小字符串拼接即可。现在问题就在于拆分的方法。
拆分的目的在于每次从多位的整数中分离出一位小于基整数,对于769,拆分的过程就是:“769” = “76” + “9” , “76” = “7” + “6” 。在分离的过程中,这个多位的整数位数朝着变成一位整数的方向发展,这就是本体的想基本结束条件演进(减小规模)
拆分可以同时使用求余数和整数除,求余数用于分离出大整数的最后一位,整数除用于保留除最后一位外的前面几位。
具体来讲,整数除是“十进制整数 // 基base”。
求余数“十进制整数 % 基base”。
例如:
769 % 10 = 9 < 10 -> “9”
769 // 10 = 76
76 % 10 = 6 < 10 -> “6”
76 // 10 = 7 < 10 -> “7”
整数就是 “7” + “6” + “9” = “769”
基本结束条件就是余数小于10。
减小规模就是整数除后的商位数小于原整数。
调用自身就是每次对整数商使用自身函数减少规模。
流程图如下:
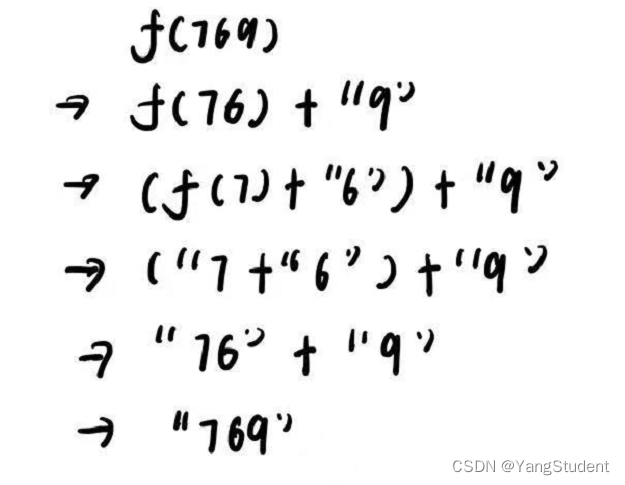
类比到十进制转为二进制,十进制转为十六进制也是一样的。
769 // 2 = 384
769 % 2 = 1 < 2 -> 1
384 // 2 = 192
384 % 2 = 0 < 2 -> 0
192 // 2 = 96
192 % 2 = 0 < 2 -> 0
96 // 2 = 48
96 % 2 = 0 < 2 -> 0
48 // 2 = 24
48 % 2 = 0 < 2 -> 0
24 // 2 = 12
24 % 2 = 0 < 2 -> 0
12 // 2 = 6
12 % 2 = 0 < 2 -> 0
6 // 2 = 3
6 % 2 = 0 < 2 -> 0
3 // 2 = 1 < 2 -> 1
3 % 2 = 1 < 2 -> 1
从下往上把字符串拼接起来
所以 769 转成 二进制 就是 1100000001
代码如下:
def to_str(number, base):
convert_str = "0123456789ABCDEF"
if number < base: # 最小结束条件
return convert_str[number]
else:
return to_str(number // base, base) + convert_str[number % base] # 向最小结束条件演化
print(to_str(769, 2))
print(to_str(769, 10))
print(to_str(769, 16))
4. 递归调用在系统中是怎么实现的
4.1 递归实现的原理
当一个函数被调用的时候,系统会把调用时的现场数据压入到系统调用栈。
每次调用,压入栈的现场数据称为栈帧。
当函数返回时,要从调用栈的栈顶取得返回地址,恢复现场,弹出栈帧,按地址返回。
4.2 Python中的递归深度限制
在调用递归算法的程序时,会遇到这样的错误:RecursionError。如下图。

解决方法:
要检查程序中是否忘记设置基本结束条件,导致无限递归。
或者向基本结束条件演进太慢,导致递归层数太多,调用栈溢出。

Python的内置的sys模块可以在Python内置的sys模块可以获取和调整最大递归深度。

递归的影视作品:
前目的地
恐怖游轮
参考文献
本文的知识来源于B站视频 【慕课+课堂实录】数据结构与算法Python版-北京大学-陈斌-字幕校对-【完结!】,是对陈斌老师课程的复习总结