[数据结构与算法]C#，哈密顿环问题（Hamiltonian Cycle problem）的算法与源程序

?

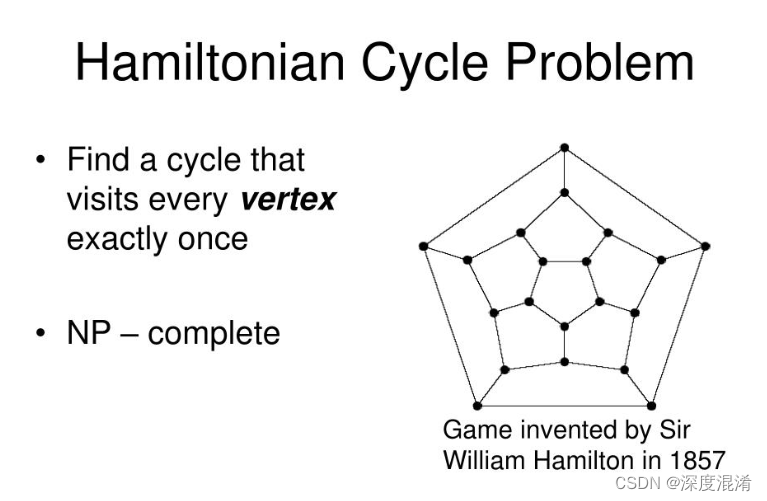
哈密顿圈问题

无向图中的哈密顿路径是一条恰好访问每个顶点一次的路径。哈密顿循环（或哈密顿回路）是一条哈密顿路径，从哈密顿路径的最后一个顶点到第一个顶点有一条边（在图中）。确定给定的图是否包含哈密顿圈。如果包含，则打印路径。以下是所需功能的输入和输出。

输入：

二维数组图[V][V]，其中V是图中的顶点数，图[V][V]是图的邻接矩阵表示。如果从i到j有一条直边，则值图[i][j]为1，否则图[i][j]为0。

在无向图中，哈密顿路径是一条恰好访问每个顶点一次的路径，哈密顿圈或回路是一条哈密顿路径，即从最后一个顶点到第一个顶点有一条边。

在这个问题中，我们将尝试确定一个图是否包含哈密顿圈。当存在哈密顿循环时，也打印该循环。

算法思路

给定一个图G=（V，E），我们必须使用回溯方法找到哈密顿回路。我们从任意顶点开始搜索，比如“a”。该顶点“a”成为隐式树的根。部分解的第一个元素是要构造的哈密顿循环的第一个中间顶点。按字母顺序选择下一个相邻顶点。如果在任何阶段，任何任意顶点与顶点“a”以外的任何顶点进行循环，则我们称达到了死端。在这种情况下，我们回溯一步，然后再次开始搜索，选择另一个顶点并从部分回溯元素；必须移除溶液。如果得到一个哈密顿循环，则使用回溯的搜索是成功的。

From backtracking, the vertex adjacent to 'e' is b, c, d, and f from which vertex 'f' has already been checked, and b, c, d have already visited. So, again we backtrack one step. Now, the vertex adjacent to d are e, f from which e has already been checked, and adjacent of 'f' are d and e. If 'e' vertex, revisited them we get a dead state. So again we backtrack one step.

Now, adjacent to c is 'e' and adjacent to 'e' is 'f' and adjacent to 'f' is 'd' and adjacent to 'd' is 'a.' Here, we get the Hamiltonian Cycle as all the vertex other than the start vertex 'a' is visited only once. (a - b - c - e - f -d - a).

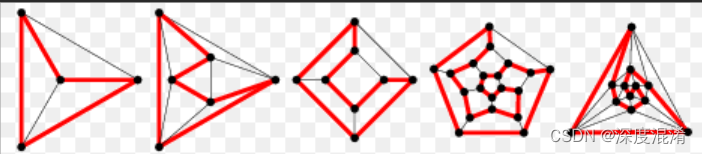
参考：

C#，图（Graph）的数据结构设计与源代码https://blog.csdn.net/beijinghorn/article/details/125133711

源代码(POWER BY TRUFFER)：

using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
	public partial class Graph
	{
		private bool IsSafe(int v, int[] path, int pos)
		{
			if (Matrix[path[pos - 1], v] == 0)
			{
				return false;
			}
			for (int i = 0; i < pos; i++)
			{
				if (path[i] == v)
				{
					return false;
				}
			}
			return true;
		}

		private bool Hamiltonian_Cycle_Utility(ref int[] path, int pos)
		{
			if (pos == Node_Number)
			{
				if (Matrix[path[pos - 1], path[0]] == 1)
				{
					return true;
				}
				else
				{
					return false;
				}
			}

			for (int v = 1; v < Node_Number; v++)
			{
				if (IsSafe(v, path, pos))
				{
					path[pos] = v;

					if (Hamiltonian_Cycle_Utility(ref path, pos + 1) == true)
					{
						return true;
					}
					path[pos] = -1;
				}
			}

			return false;
		}

		public bool Hamiltonian_Cycle(out int[] path)
		{
			path = new int[Node_Number];
			for (int i = 0; i < Node_Number; i++)
			{
				path[i] = -1;
			}

			path[0] = 0;
			if (Hamiltonian_Cycle_Utility(ref path, 1) == false)
			{
				return false;
			}

			return true;
		}
	}

	public static partial class GraphDrives
	{
		private static string PrintPath(int[] path)
		{
			StringBuilder sb = new StringBuilder();
			sb.AppendLine("Solution Exists: Following is one Hamiltonian Cycle<br>");
			for (int i = 0; i < path.Length; i++)
			{
				sb.Append(path[i] + " -> ");
			}
			sb.Append(path[0] + " ");

			return sb.ToString();
		}

		public static string HamiltonianCycle()
		{
			StringBuilder sb = new StringBuilder();

			int[,] graph1 = {
				{ 0, 1, 0, 1, 0 },
				{ 1, 0, 1, 1, 1 },
				{ 0, 1, 0, 0, 1 },
				{ 1, 1, 0, 0, 1 },
				{ 0, 1, 1, 1, 0 }
			};

			Graph g1 = new Graph(graph1);

			if (g1.Hamiltonian_Cycle(out int[] path1))
			{
				sb.AppendLine(PrintPath(path1));
			}
			else
            {
				sb.AppendLine("Solution does not exist");
			}

			int[,] graph2 = {
				{ 0, 1, 0, 1, 0 },
				{ 1, 0, 1, 1, 1 },
				{ 0, 1, 0, 0, 1 },
				{ 1, 1, 0, 0, 0 },
				{ 0, 1, 1, 0, 0 }
			};

			Graph g2 = new Graph(graph2);

			if (g2.Hamiltonian_Cycle(out int[] path2))
			{
				sb.AppendLine(PrintPath(path2));
			}
			else
			{
				sb.AppendLine("Solution does not exist");
			}

			return sb.ToString();
		}
	}
}