一、实验目的:
(1)掌握最大流算法思想。
(2)学会用最大流算法求解应用问题。
二、问题描述:
- 有m篇论文和n个评审,每篇论文需要安排a个评审,每个评审最多评b篇论文。请设计一个论文分配方案。
- 要求应用最大流解决上述问题,画出m=10,n=3的流网络图并解释说明流网络图与论文评审问题的关系。
- 编程实现所设计算法,计算a和b取不同值情况下的分配方案,如果没有可行方案则输出无解。
三、算法设计原理:
1.二分图的构建
将每一篇论文、每一位评审都抽象成为一个点,可以得到一个论文的点集和一个评审的点集。如下图左边十个点的集合表示论文,右边三个点表示三位评审。
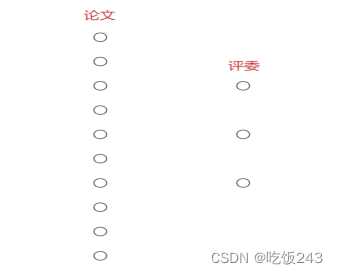
图1
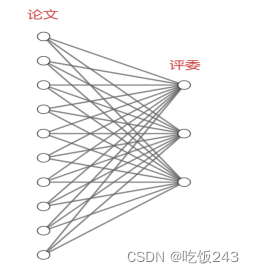
图2
在二分图中一条边表示一篇论文和一个评审的匹配。那么画出这个解决方案的二分图就可以得到图2所示的一个二分图。
2.搭建流网络
(1)加入源点和汇点
因为要使用最大流算法解决问题,所以需要流网络,而流网络需要一个源点和一个汇点。
在论文的左边加入一个源点S, 在评委的右边加入汇点T,如下图所示
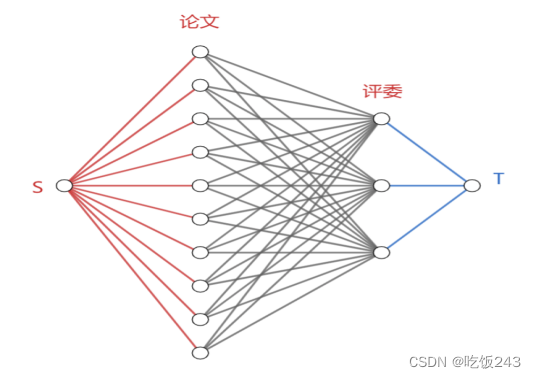
图3 加入源点和汇点
(2)容量限制
1)因为每篇论文都需要a位评审,所以源点和论文之间的容量限制应该设置为a。
2)因为每个评委最多能评b篇论文,所以评审和汇点之间的容量限制应设置为b。
3)因为评委和论文是多对多的关系,但每个评委只会评阅一篇论文一次,所以论文和评委之间的容量限制为1,1表示评委评阅了该篇论文,0表示没有评阅。
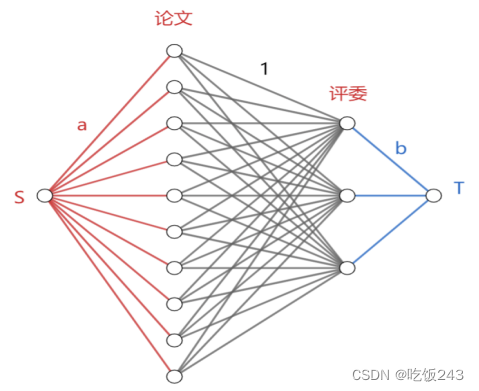
图4 加入了容量限制
3.判断是否存在可行解
有m篇论文和n个评审,每篇论文需要安排a个评审,每个评审最多评b篇论文。
(1) a≤n 流量守恒
(2)a × m ≤ b × n 流量守恒
4.FF方法
(1)方法思想
建立残留网络,在残留网络上找增广路径,然后沿着增广路径增广流,增广流由路径上的最小容量限制,当找不到增广路径时结束算法。
5.EK算法
(1)算法思想
通过bfs寻找最短的增广路,求得增广路上容量限制的最小值,然后更新残留网络和流网络,直到找不到增广路。
(2)算法流程
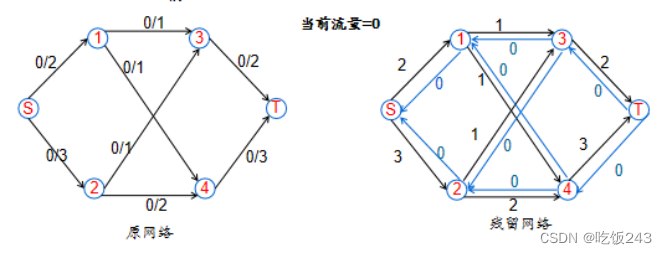
图5 建立残留网络
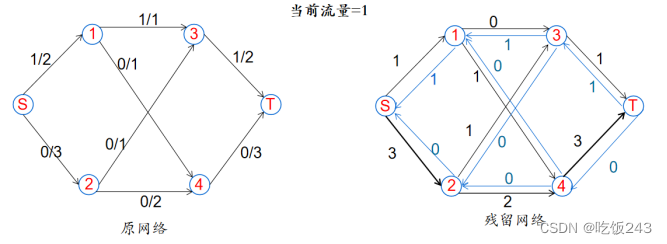
图6 寻找第一条增广路
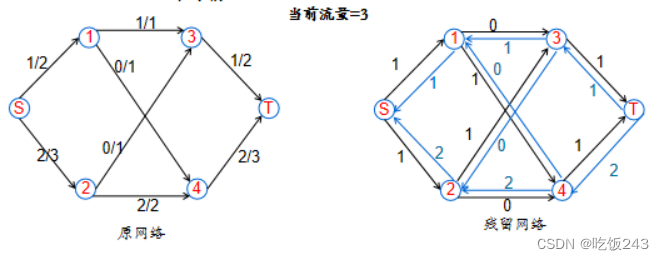
图7 更新残留网络并寻找第二条增广路
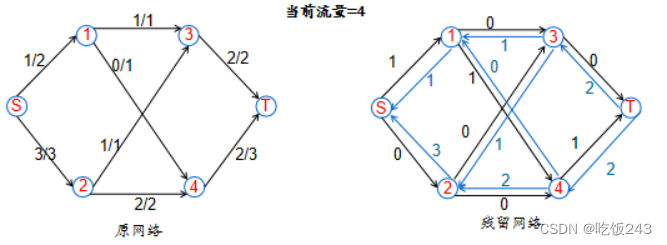
图8 更新残留网络并寻找第三条增广路
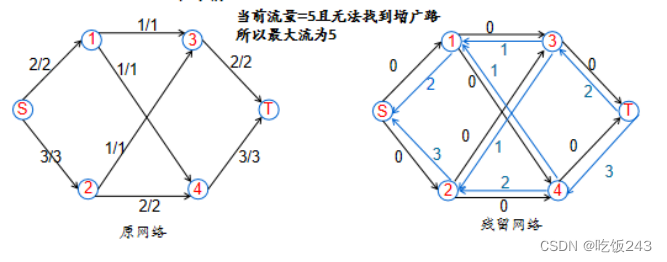
图9 更新残留网络并发现找不到增广路,结束算法
(3)伪代码
EK()
init() //初始化
ans = 0
// 通过bfs寻找最短的增广路
while (bfs()) do:
ans += d[T] //更新当前流量
// 更新残留网络
return ans
(4)时间复杂度为 O ( V E 2 ) O(VE^2) O(VE2),V为点数,E为边数
6.dinic算法
(1)算法思想
在残留网络上使用bfs进行分层,然后在分层图上找增广路,每次找增广路的时候,都只找比当前点层数多1的点进行增广,即DFS,可以实现多路增广。
(2)算法流程
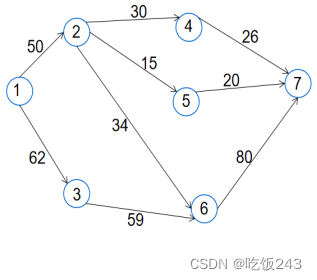
图10 原网络
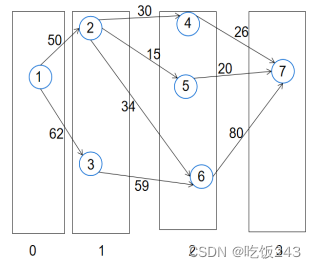
图11 分层图
1)分层图的作用:防止在环上进行循环,降低效率
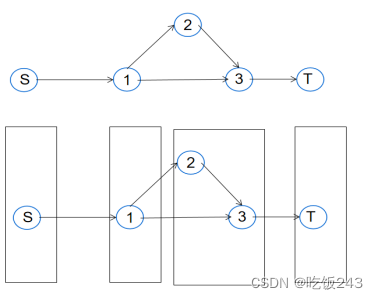
图12 分层图的作用
2)多路增广
每次找到一条增广路的时候,如果残余流量没有用完,可以利用残余部分流量,继续找增广路,从而实现多路增广。
如下图13所示,对于1发送到2号点的流量为50,然后对路径2->4-> 7进行增广,之后2号点流量还剩下20,接着对路径2 -> 5 -> 7进行增广,2号点流量还剩下5,再将剩余的流量发送到2 -> 6 -> 7这条路径上,从而实现多路增广
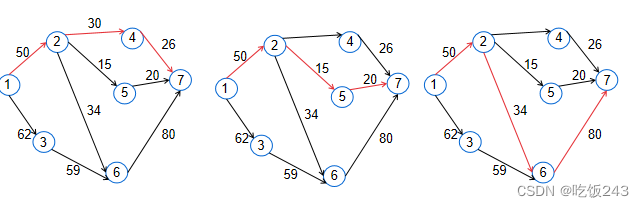
图13 多路增广
3)当前弧优化
如果一条边已经被增广过并且达到饱和,下一次进行增广的时候,可以跳过这些边。
如图14,先增广路径2 ->4 和2->5并且这两条边达到饱和,那么在增广路径3->5的时候,不再需要考虑上面那条边,直接从下面的边开始。
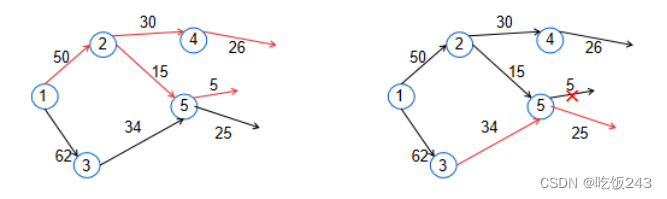
图14 当前弧优化
(3)伪代码
dinic()
ans = 0
flow = 0
while bfs() do
while flow = dfs(S) do
ans += flow
dfs(u, limit)
flow = 0
如果u是终点,返回limit
// 多路增广+当前弧优化
for i = cur[u] to i = -1 do
cur[u] = i // 更新当前弧
ver = e[i]
// 符合分层图且容量大于0
if depth[ver] == depth[ver]+1 && f[i] do
t = dfs(ver, min(f[i], limit-flow))
// 费点优化
if(!t) depth[ver] = -1
更新残留网络和最大流
return flow
(4)时间复杂度为: O ( V 2 E ) O(V^2E) O(V2E) V为点数,E为边数
四、实验结果分析:
1)a为变量
| a | EK(ms) | dinic(ms) |
|---|---|---|
| 5 | 920.348800 | 1.254800 |
| 10 | 2523.258500 | 1.510000 |
| 15 | 4769.536000 | 1.919100 |
| 20 | 7816.660300 | 2.426900 |
| 25 | 11726.257500 | 2.809200 |
n = m = 500, b = 25
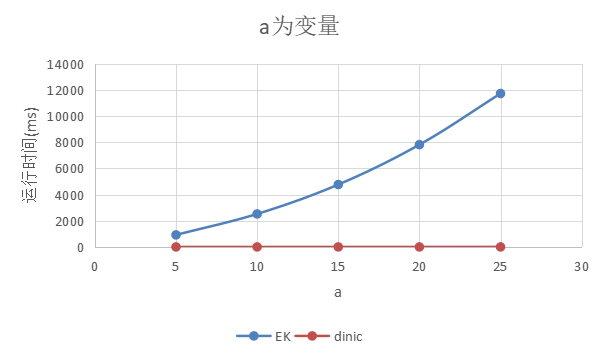
结论:a增大,对EK影响较大,对 dinic 影响不大
2)b为变量
| b | EK(ms) | dinic(ms) |
|---|---|---|
| 5 | 2447.235600 | 2.922800 |
| 10 | 1536.876900 | 1.547700 |
| 15 | 1157.089600 | 1.253300 |
| 20 | 1015.292000 | 1.182800 |
| 25 | 912.668700 | 1.010900 |
n = m = 500, a = 5
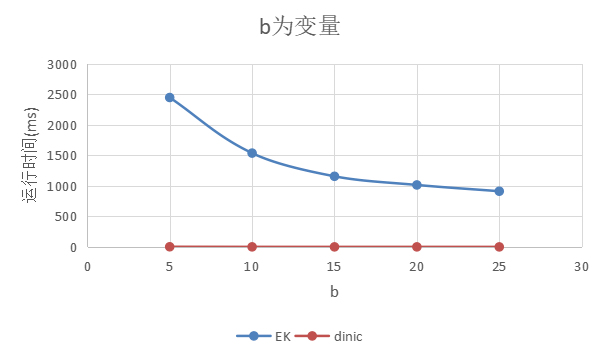
结论:b增大,对EK影响较大,对dinic 影响不大
3)n为变量
| n | EK(ms) | dinic(ms) |
|---|---|---|
| 100 | 30.419000 | 0.381000 |
| 200 | 124.254100 | 0.337900 |
| 300 | 314.305800 | 0.457200 |
| 400 | 559.755100 | 0.748700 |
| 500 | 973.228800 | 1.014700 |
m = 500, b = 25, a = 5
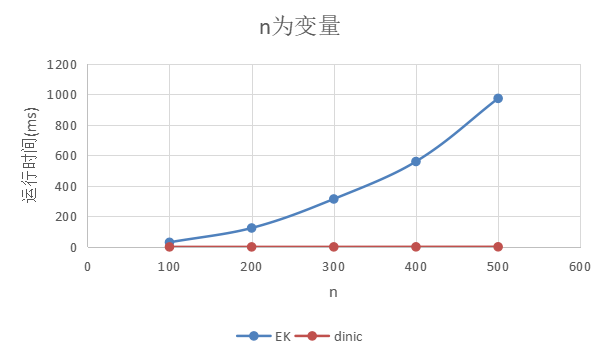
结论:n增大,对EK影响较大,对dinic 影响不大
4)m为变量
| m | EK(ms) | dinic(ms) |
|---|---|---|
| 100 | 383.482400 | 0.676000 |
| 200 | 567.874100 | 0.589700 |
| 300 | 636.335200 | 0.811600 |
| 400 | 769.059300 | 0.890400 |
| 500 | 913.823400 | 1.032600 |
n = 500, b = 25, a = 5
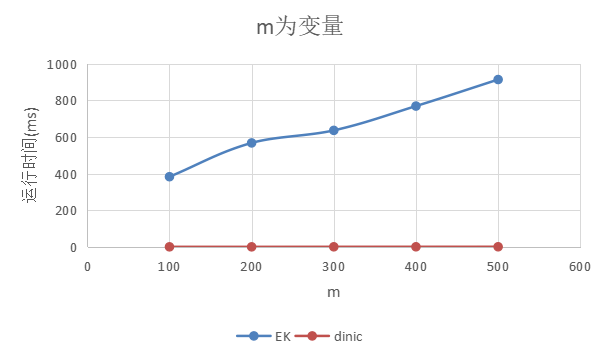
结论:m增大,对EK影响较大,对dinic 影响不大
五、实验结论:
1.最大流问题的几个增广路算法时间复杂度均为较宽松的上界,一般来说实际效率会比理论时间效率高很多。
六、补充 y总课程截图

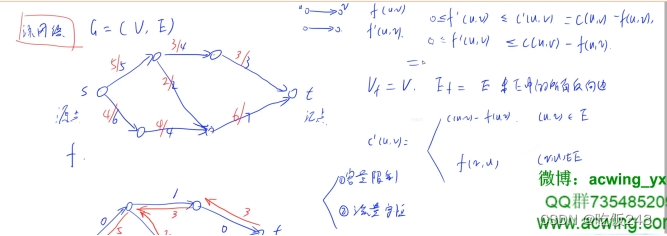


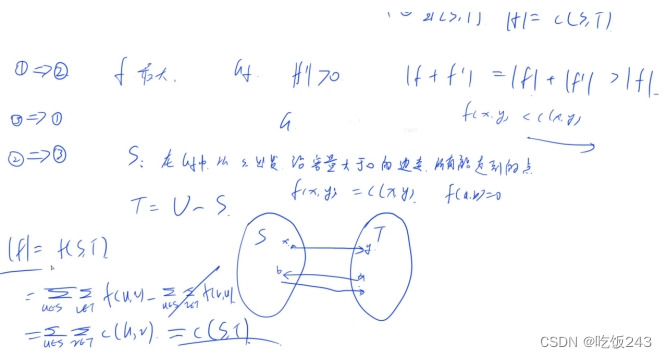

代码,不建议CV
https://download.csdn.net/download/weixin_50325452/85692679