Car-Like小车移动机器人控制实验(Car-Like)
下载链接https://download.csdn.net/download/yjw0911/85677358
下载点击链接
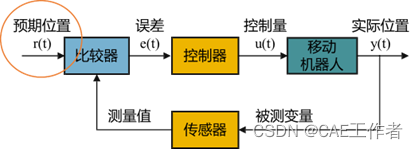
实验目的:把移动机器人运动看成单纯控制问题,提升学生的移动机器人基础理论水平和专业技能。在构建Car-Like小车运动曲线规划、运动学、动力学、控制器模型的基础上,完成Car-Like小车跟踪曲线仿真。
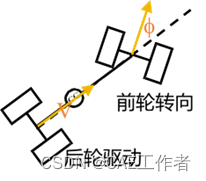
Car-Like小车,由直流电机通过减速齿轮带动后轮旋 转驱动小车以速度V前进;由舵机驱动前轮转向,转向角为𝜙。
实验要求:
在理解基本原理基础上,使用Matlab和Simulink,编制各功能模块,实现移动机器人运动控制仿真,包括路径曲线规划、运动学模型、动力学模型、控制算法设计。
一、平面曲线规划:N个控制点的B样条曲线
规划一条由起点到终点,合乎要求光滑曲线。给定一组控制点而得到一条曲线,曲线大致形状由这些 点予以控制。一般用得多是三次B样条曲线。
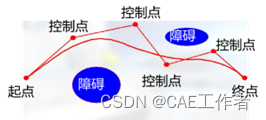
如小车移库问题:规划一条由起点出发 到达终点的光滑曲线
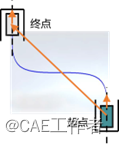
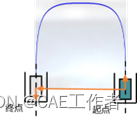
过控制点的B样条曲线
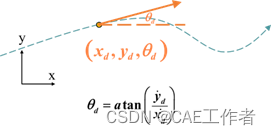
平面曲线规划,机器人位置可以用其二维组坐标(x,y)的参数方程描述。
给定四个控制点[C1,C2,C3,C4],则样条曲线为P(s),参数s满足0≤s≤1,可以看成是归一化路程。
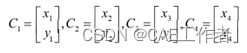
(1)四个控制点:
四个样条函数:f1 ?s?, f2 ?s?, f3 ?s?, f4 ?s?
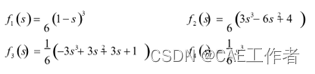
给定四个控制点[C1,C2,C3,C4],则样条曲线为P(s),参数s满足0≤s≤1,可以看成是归一化的路程。
P(s) =f1(s)C1 +f2(s)C2 +f3(s)C3 +f4(s)C4
Matlab程序文件:demomooc1.m
(2)五个控制点的B样条曲线
如果给定五个控制点[C1,C2,C3,C4,C5],则决定了两条样条曲线为P1(s),P2(s)。
P1(s)=f1 (s)C1 +f2 (s)C2 +f3 (s)C3 +f4 (s)C4 (0≤s≤1)
P2(s) =f1 (s)C2 +f2 (s )C3 +f3 (s)C4 +f4 (s)C5 (0≤s≤1)
控制点: 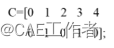
程序片段:
P1s=C(:,1)*f1s+C(:,2)*f2s+C(:,3)*f3s+C(:,4)*f4s;
P2s=C(:,2)*f1s+C(:,3)*f2s+C(:,4)*f3s+C(:,5)f4s;
%绘制控制点及B样条曲线
figure(1)
plot(C(1,:),C(2,:),'r’,P1s(1,:),P1s(2,:),‘b’,P2s(1,:),P2s(2,:),‘c’);
legend(‘控制点’,‘第一段’,‘第二段’)
(3)N个控制点的B样条曲线
如果给定N 个控制点[C1,C2,C3,…,CN],则决定了(N-3)条样条曲线为P1(s),P2(s),…,P(N-3)(s)
P1(s)=f1 (s)C1 +f2 (s)C2 +f3 (s)C3 +f4 (s)C4
P2(s) =f1 (s)C2 +f2 (s )C3 +f3 (s)C4 +f4 (s)C5
?
PN -3 (s) =f1 (s)CN -3+f2 (s)CN -2 +f3 (s)CN -1+ f4 (s)CN
Matlab程序文件:demomooc3.m
(4)过起点和终点的B样条曲线
过起点的B样条曲线:通过增加额外控制点来保证P(s)过起点C1
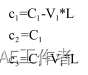
过终点的B样条曲线:通过增加额外控制点来保证P(s)过终点CN
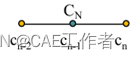
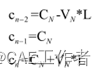
V1,VN表示小车过C1,CN速度方向的单位向量;L为合适正常数,可以取为小车车长一半。
原来的控制点: 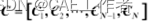
增广后的控制点: 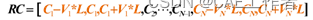
Matlab程序文件:demomooc4.m
(5)轨迹曲线的曲率
曲线曲率K是曲线弯曲程度一种度量,曲率K越大曲线 越弯曲,小车跟踪更为困难,可以用曲线曲率K评价轨迹曲线的好坏。
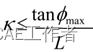
fmax前轮的最大转向角,轨迹曲率越大,表示小车轨迹越弯曲,跟踪更为困难。
实验:demoexp7.m,改变控制点减小曲线曲率,鼠标左键改变控制点,鼠标右键退出得到新控制点P,得到合理的曲线规划。
二、Car-Like小车运动学仿真
(1)Car-Like小车运动学模型
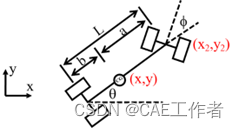
a为重心到前轮中心距离,b为重心到后轮中心距离,L为前轮中心与后轮中心的距离,显然L=a+b,设小车重心坐标为(x,y),则后轮中心坐标为(x1,y1),前轮中心坐标为(x2,y2)。
后轮位置、速度关系: 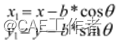
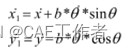
轮子运动特性,后轮没有侧滑
等等