文章目录
堆排序是原地,时间复杂度为O(nlogn)。快速排序也是如此,为什么实际软件开发快速排序性能要比堆排序要好?
1. 如何理解“堆”?
特点:
- 堆是一个完全二叉树;
- 每个节点大于等于或小于等于其左右子树的值。前者叫大顶堆,后者叫小顶堆。
2.如何实现一个堆?
完全二叉树可以用数组实现堆,比较省内存,因为不用存指针,直接根据索引计算。
节点索引i,其左节点为2i+1,右节点为2i+2。
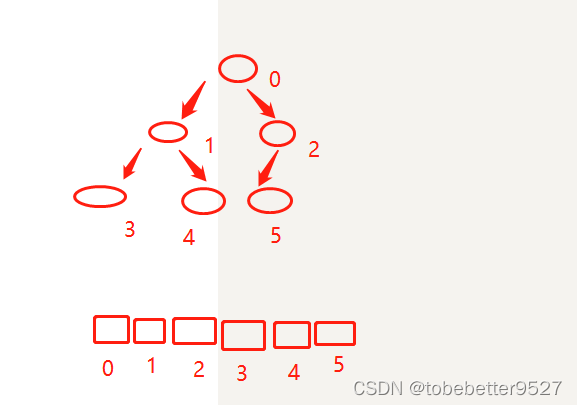
2.1 往堆中插入一个元素
插入一个新元素后,需要继续满足堆的两个要求,为此需要堆化(heapify),堆化有上到下,下到上两种方法。
2.1.1 从下到上堆化
案例:
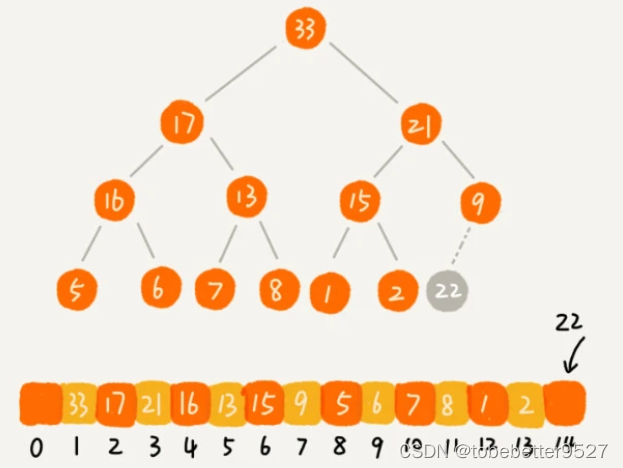
过程:
public class Heap {
private int[] a; // 数组,从下标1开始存储数据
private int n; // 堆可以存储的最大数据个数
private int count; // 堆中已经存储的数据个数
public Heap(int capacity) {
a = new int[capacity + 1];
n = capacity;
count = 0;
}
public void insert(int data) {
if (count >= n) return; // 堆满了
++count;
a[count] = data;
int i = count;
while (i/2 > 0 && a[i] > a[i/2]) { // 自下往上堆化
swap(a, i, i/2); // swap()函数作用:交换下标为i和i/2的两个元素
i = i/2;
}
}
}
我的版本:
public class Class28_Heap {
int[] arr;
// 存储最大个数
int n;
// 当前存储的个数
int size;
public Class28_Heap(int capacity) {
this.arr = new int[capacity];
this.n = capacity;
}
/**
* 构建大顶堆
*
* @param value
*/
public void insert(int value) {
if (size > n) {
return;
}
size++;
arr[size - 1] = value;
int i = size - 1;
while (i >= 0 && arr[i] > arr[(i - 1) / 2]) {
swap(arr, i, (i - 1) / 2);
i = (i - 1) / 2;
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
Class28_Heap heap = new Class28_Heap(10);
heap.insert(10);
heap.insert(8);
heap.insert(9);
heap.insert(2);
heap.insert(5);
heap.insert(13);
System.out.println("done ");
}
}
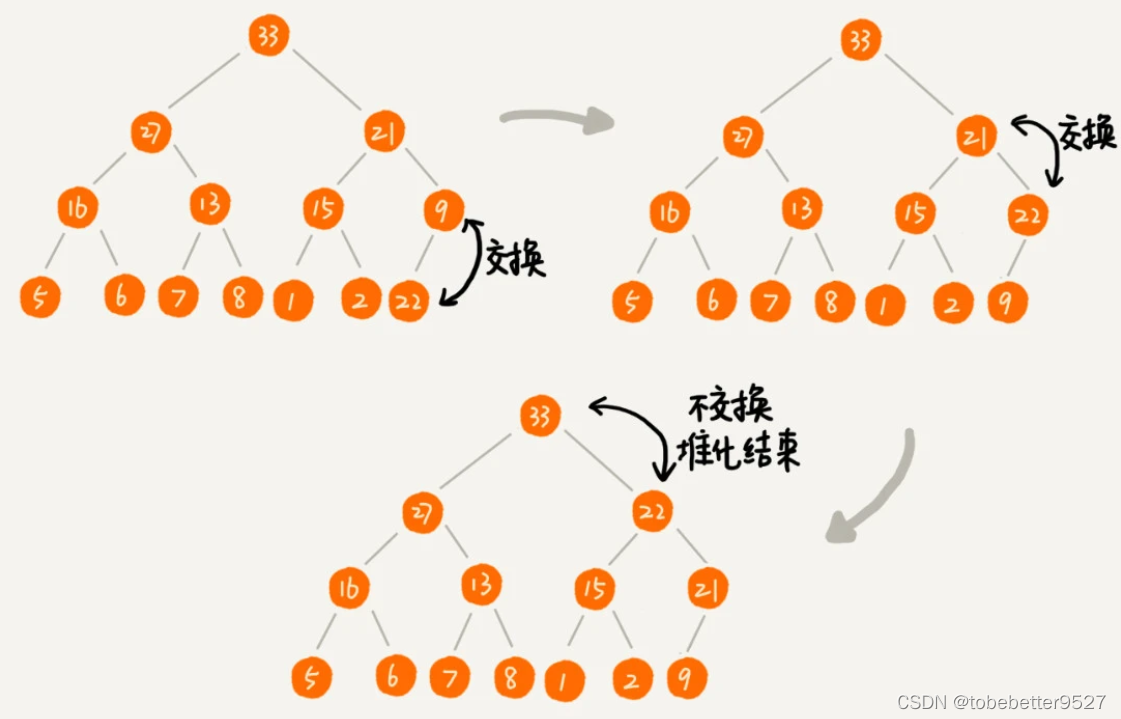
2.2 删除堆顶元素
2.2.1 从上往下堆化
思路1问题:
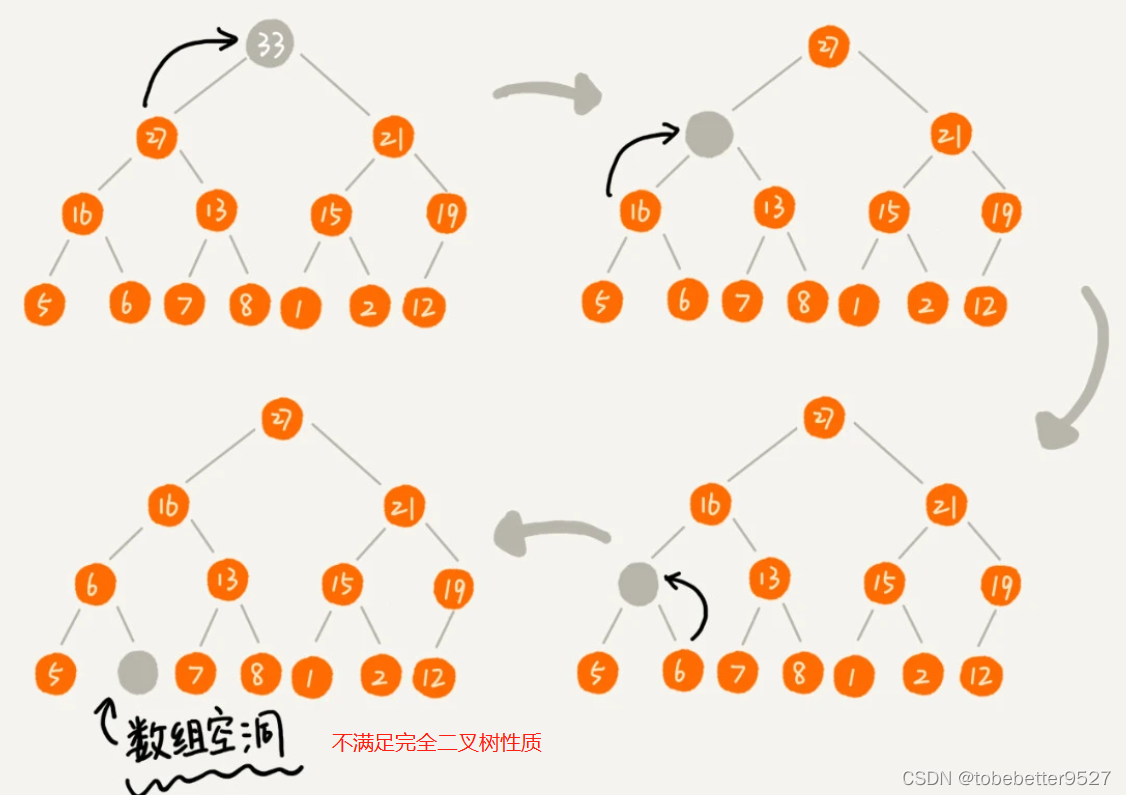
改进:
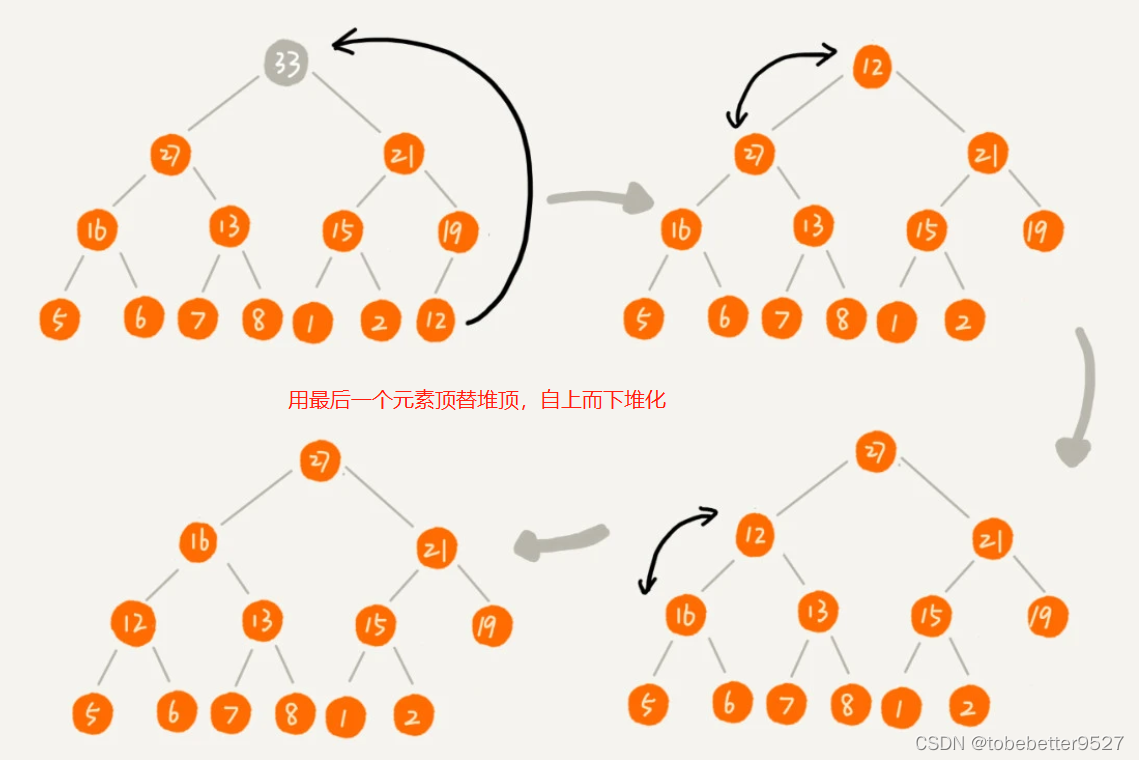
public void removeMax() {
if (count == 0) return -1; // 堆中没有数据
a[1] = a[count];
--count;
heapify(a, count, 1);
}
private void heapify(int[] a, int n, int i) { // 自上往下堆化
while (true) {
int maxPos = i;
if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
if (maxPos == i) break;
swap(a, i, maxPos);
i = maxPos;
}
}
我的版本:
public void removeMax() {
if (size == 0) {
return;
}
arr[0] = arr[size - 1];
// 该位置的值需要移除
arr[size - 1] = 0;
size--;
heapify(arr, size, 0);
}
private void heapify(int[] arr, int size, int i) {
while (true) {
int maxPos = i;
if ((i * 2 + 1) < n && arr[i] < arr[(i * 2 + 1)]) {
maxPos = 2 * i + 1;
}
if ((i * 2 + 2) < n && arr[maxPos] < arr[(i * 2 + 2)]) {
maxPos = 2 * i + 2;
}
// 加入i节点的值比左右节点都大,就可以终止了
if (maxPos == i) {
break;
}
swap(arr, maxPos, i);
// 继续往下堆化
i = maxPos;
}
}
3. 如何基于堆实现排序?
堆排序是原地排序,时间复杂度非常稳定O(nlog n)。
3.1 建堆
两种实现思路:
- 参考往堆中插入数据,从前往后处理数组,每插入一个数据,从下往上堆化;
- 从后往前处理数组,从上往下堆化。
举第二种例叶:子节点只能自己跟自己比较,所以可以忽略处理。
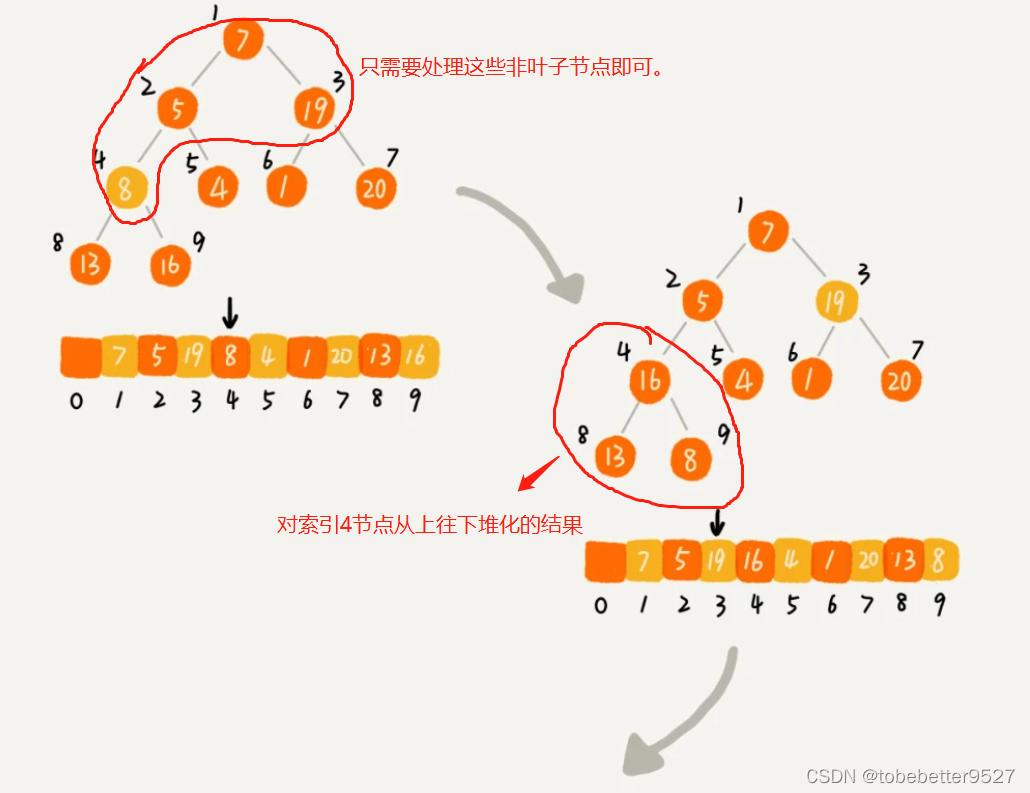
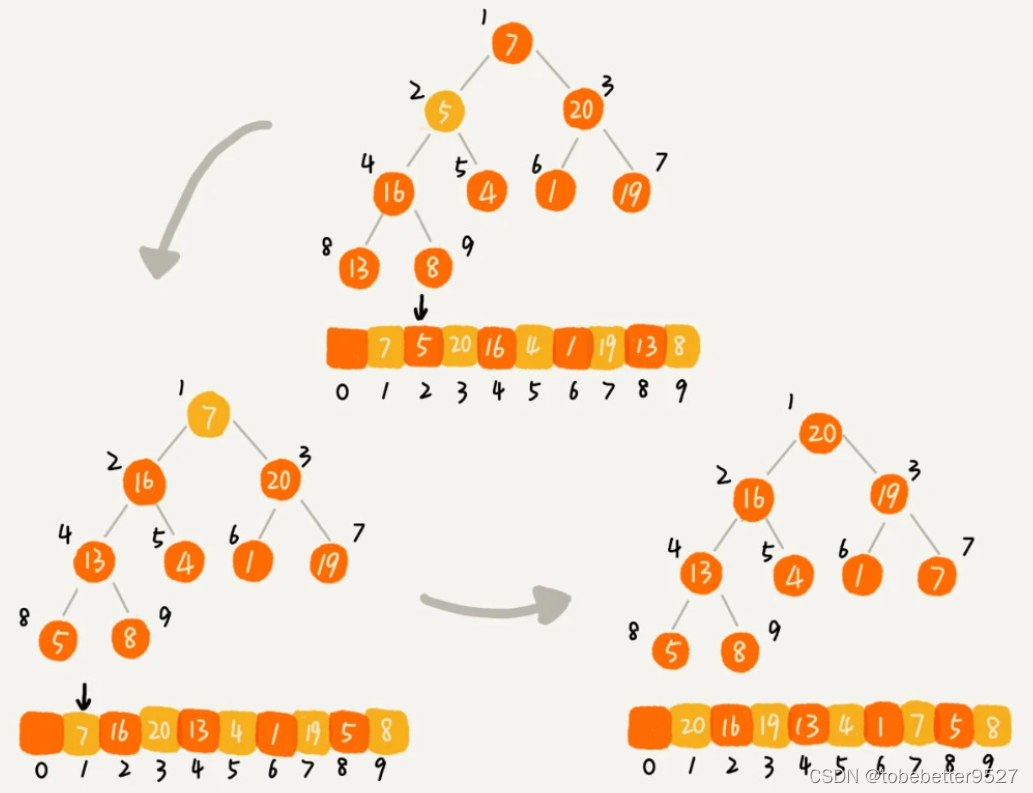
private static void buildHeap(int[] a, int n) {
for (int i = n/2; i >= 1; --i) {
heapify(a, n, i);
}
}
private static void heapify(int[] a, int n, int i) {
while (true) {
int maxPos = i;
if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
if (maxPos == i) break;
swap(a, i, maxPos);
i = maxPos;
}
}
我的版本:
private static void heapify(int[] arr, int size, int i) {
while (true) {
int maxPos = i;
if ((i * 2 + 1) < size && arr[i] < arr[(i * 2 + 1)]) {
maxPos = 2 * i + 1;
}
if ((i * 2 + 2) < size && arr[maxPos] < arr[(i * 2 + 2)]) {
maxPos = 2 * i + 2;
}
// 加入i节点的值比左右节点都大,就可以终止了
if (maxPos == i) {
break;
}
swap(arr, maxPos, i);
// 继续往下堆化
i = maxPos;
}
}
public void buildHeap(int[] arr) {
int n = arr.length;
for (int i = ((n - 1) - 1) / 2; i >= 0; i--) {
heapify(arr, n, i);
}
}
3.1.1 建堆的时间复杂度
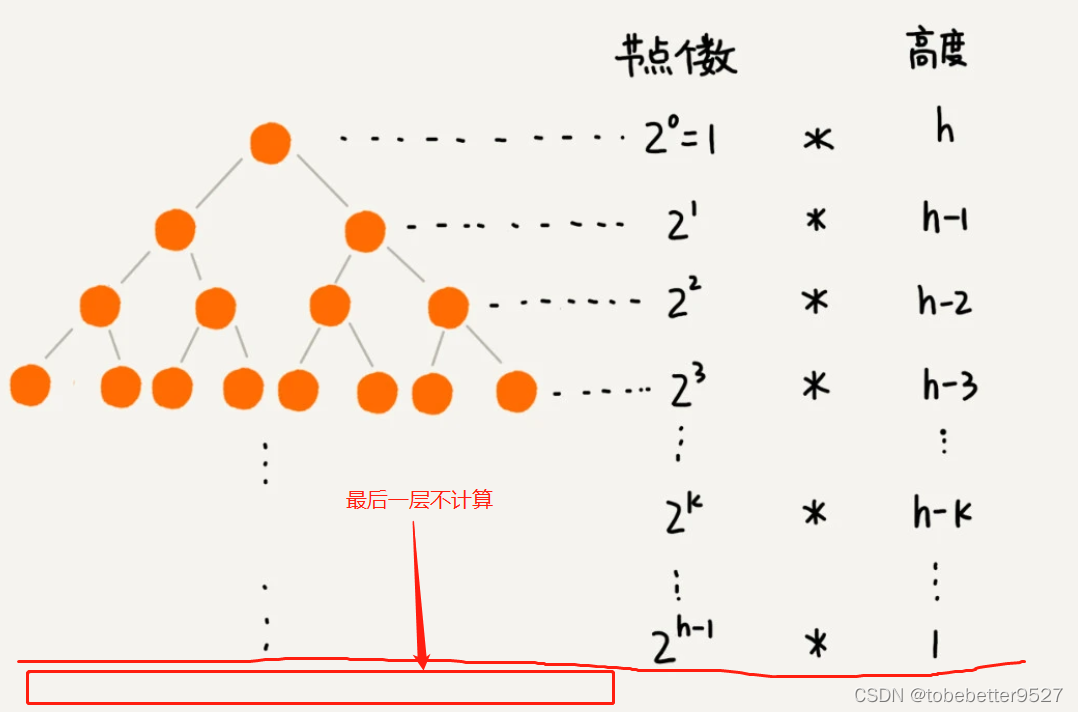
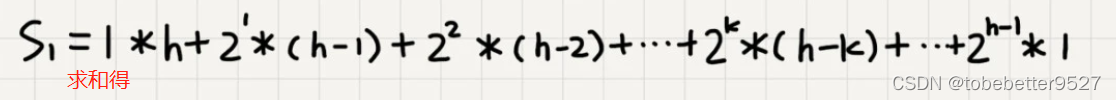

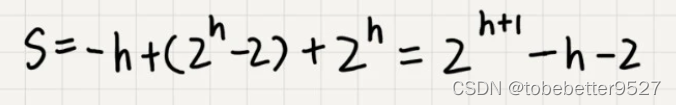
h=logn,带入公式:
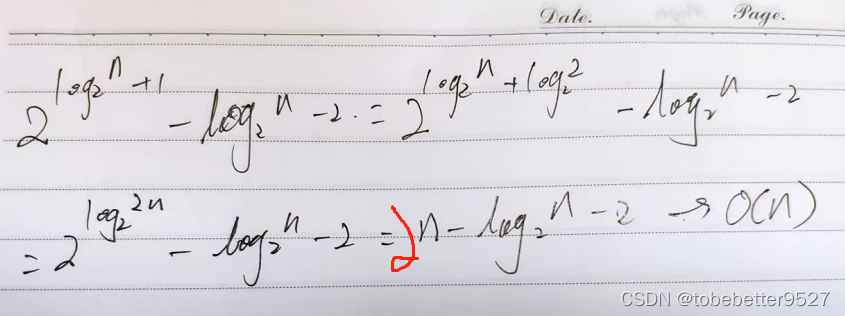
3.2 排序
建堆完成,堆顶是最大元素,与组后一个元素交换位置,将剩下n-1个元素重新建堆,以此类推,直到组后一个元素。得到数组就是有序的。
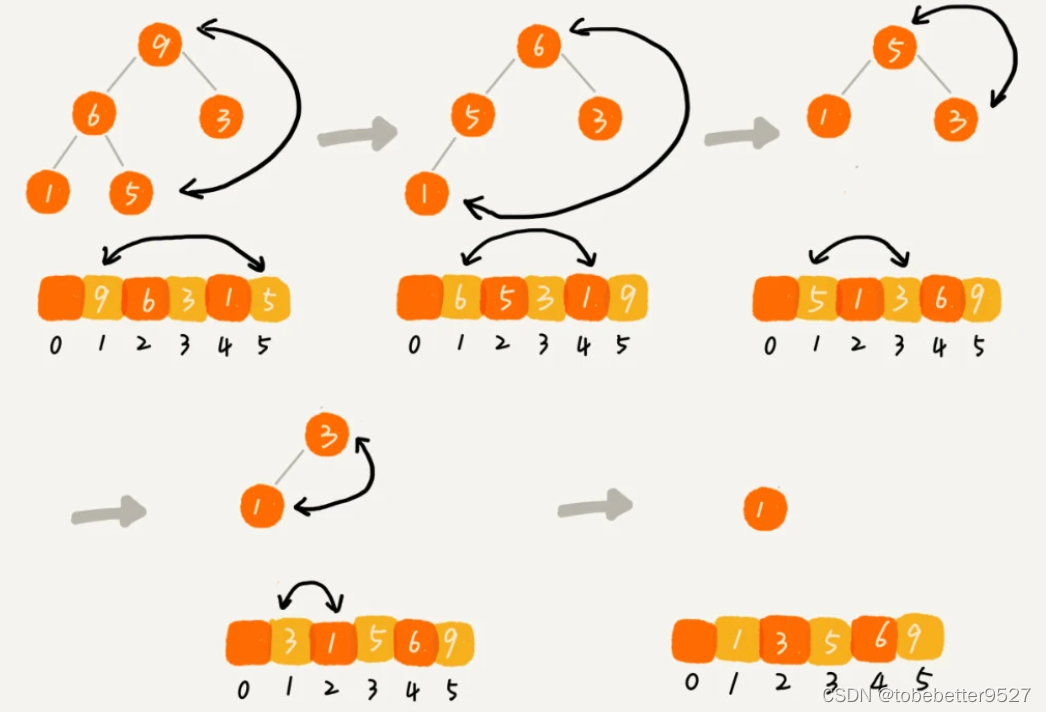
// n表示数据的个数,数组a中的数据从下标1到n的位置。
public void sort(int[] a, int n) {
buildHeap(a, n);
int k = n;
while (k > 1) {
swap(a, 1, k);
--k;
heapify(a, k, 1);
}
}
我的版本:
public static void sort(int[] arr) {
buildHeap(arr);
int k = arr.length - 1;
while (k >= 0) {
swap(arr, 0, k);
k--;
heapify(arr, k + 1, 0);
}
}
总结:堆排序是原地,时间复杂度O(nlog n),不稳定的排序算法。
4. 解答开篇
- 堆排序数据访问的方式没有快速排序友好,对于快速排序来说,数据是顺序访问的。而对于堆排序来说,数据是跳着访问的,对CPU缓存是不友好的。
- 对于同样的数据,在排序过程中,堆排序算法的数据交换次数要多于快速排序。