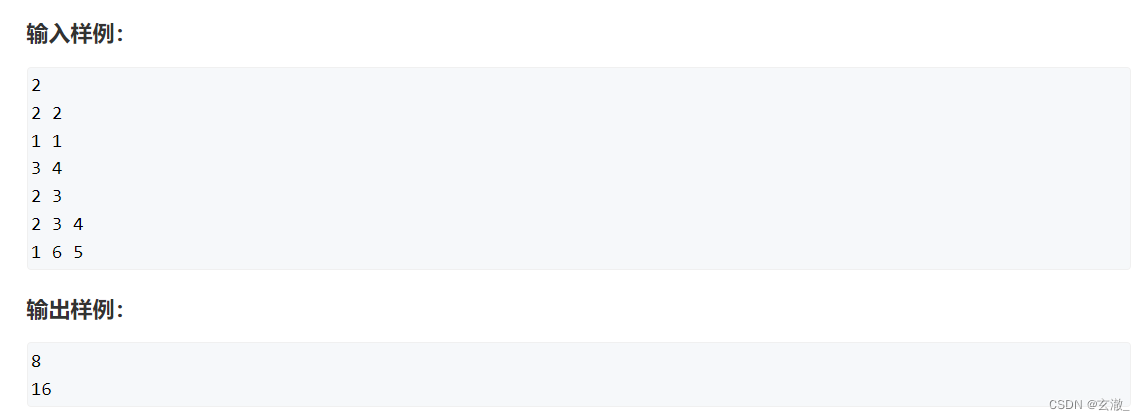
动态规划
动态规划算法把原算法视作若干个重叠子问题的逐层递进,每个子问题的求解过程都构成一个“阶段”。在完成前一个阶段的计算之后,动态规划才会执行下一个阶段的计算。
为了保证这些计算能够按顺序、不重复地进行,动态规划要求已经求解的子问题不受后续阶段的影响。这个条件也叫“无后效性”。换言之,动态规划对状态空间的遍历构成一张有向无环图,遍历顺序就是该有向无环图的一个拓扑序。有序无环图中的节点对应问题中的“状态”,图中的边则是对应状态之间的“转移”,转移的选取就是动态规划中的“决策”。
在很多情况下,动态规划用于求解最优化问题。此时,下一阶段的最优解应该能够由前前面各阶段的子问题的最优解求出。这个条件被称为“最优子结构性质”。
“状态”、“阶段”和“决策”是构成动态规划算法的三要素,而“子问题重叠性”,“无后效性”和“最优子结构性”是问题能用动态规划求解的三个基本条件。
动态规划算法把相同的计算过程作用于各阶段的同类子问题,就好像把一个固定的公式套在格式相投的若干输入数据上运行。因此,我们一般只需要定义出DP的计算过程,就可以编程实现了,这个计算过程就称为“状态转移方程”。
闫式思考法
从集合的角度来思考问题:?

例题:AcWing 1015. 摘花生
集合含义:所有从? ?走到?
?的所有路线的最大值?
在状态计算中,很重要的划分依据:“最后”
集合的划分依据:1.不重 2.不漏(在不重复这一点是,可以出现重复算,因为最后是取子集的最最值)

AC代码?
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110;
int n, m;
int w[N][N];
int f[N][N];
int main()
{
int T; cin >> T;
while(T -- )
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
scanf("%d", &w[i][j]);
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
f[i][j] = max(f[i][j - 1], f[i - 1][j]) + w[i][j];
cout << f[n][m] << endl;
}
return 0;
}例题:AcWing 1018. 最低通行费?
跟上面的摘花生的是类似的题目类型。多了时间上面的限制(?
?)。
这个时间上面的限制 等价于 不走回头路
由于所求的是最小值,这道题在求解的时候需要对边界进行初始化。
AC代码
#include <iostream> #include <cstring> using namespace std; const int N = 210, INF = 0x3f3f3f3f; int n; int w[N][N]; int f[N][N]; int main() { cin >> n; for(int i = 1; i <= n; i ++ ) for(int j = 1; j <= n; j ++ ) scanf("%d", &w[i][j]); for(int i = 1; i <= n; i ++ ) for(int j = 1; j <= n; j ++ ) if(i == 1 && j == 1) f[i][j] = w[i][j]; else { f[i][j] = INF; if(i > 1) f[i][j] = min(f[i][j], f[i - 1][j] + w[i][j]); if(j > 1) f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]); } cout << f[n][n] << endl; return 0; }
例题:AcWing 1027. 方格取数
输入样例:
8 2 3 13 2 6 6 3 5 7 4 4 14 5 2 21 5 6 4 6 3 15 7 2 14 0 0 0输出样例:
67
这一题相比于前面两题,多了总共走两次这样的限制条件。?
在只走一次的情况中:
?表示的是?所有从?
?走到?
?的所有路线的最大值?
走两次的情况中:
?表示所有从?
,
?走到?
?的路径的所有集合的最大值
如何处理“同一个格子不能被重复选择”?
只有在??时,两条路径的格子才会重合?
??表示两个人同时走 k 步(横纵坐标之和)(类比摘花生)
?表示所有从??
,?
?分别走到?
?的路径的最大值


AC代码?
#include <iostream> #include <algorithm> using namespace std; const int N = 15; int n; int w[N][N]; int f[N * 2][N][N]; int main() { cin >> n; int a, b, c; while(cin >> a >> b >> c, a || b || c) w[a][b] = c; for(int k = 2; k <= n + n; k ++ ) for(int i1 = 1; i1 <= n; i1 ++ ) for(int i2 = 1; i2 <= n; i2 ++ ) { int j1 = k - i1, j2 = k - i2; if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n) { int t = w[i1][j1]; if(i1 != i2) t += w[i2][j2]; int &x = f[k][i1][i2]; x = max(x, f[k - 1][i1 - 1][i2 - 1] + t); x = max(x, f[k - 1][i1 - 1][i2] + t); x = max(x, f[k - 1][i1][i2 - 1] + t); x = max(x, f[k - 1][i1][i2] + t); } } cout << f[n + n][n][n]; return 0; }