一?点睛

邻接表是图的一种链式存储方法，其数据结构包括两部分：节点和邻接点。

用邻接表可以表示无向图，有向图和网。在此用无向图进行说明。

1?无向图

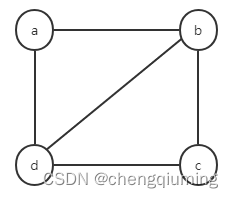
2?无向图的链接表

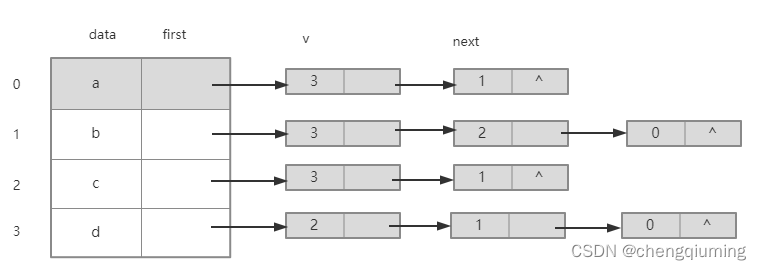
3 说明

节点 a?的邻接点是节点 b、d，其邻接点的存储下标为1、3，按照头插法（逆序）将其放入节点?a?后面的单链表中。
节点?b?的邻接点是节点 a、c、d，其邻接点的存储下标为0、2、3，按照头插法（逆序）将其放入节点?b?后面的单链表中。
节点?c?的邻接点是节点 b、d，其邻接点的存储下标为1、3，按照头插法（逆序）将其放入节点?c?后面的单链表中。
节点?d?的邻接点是节点?a、b、c，其邻接点的存储下标为0、1、2，按照头插法（逆序）将其放入节点?d?后面的单链表中。

4 无向图邻接表的特点如下

如果无向图中有?n?个节点、e?条边，则节点表中有?n?个节点，邻节点表有 2e?个节点。
节点的度为该节点后面单链表中的节点数。

二?邻接表的数据结构

1?节点

包括节点信息?data?和指向第 1?个邻接点的指针?first。

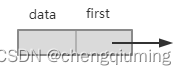
2?邻接点

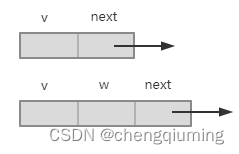
包括该邻接点的存储下标 v?和指向下一个邻接点的指针?next，如果是网的邻接点，则还需增加一个权值域?w，如下图所示。

三?算法步骤

1?输入节点数和边数。

2?依次输入节点信息，将其存储到节点数组?Vex[]?的?data 域中，将?Vex[]?first 域置空。

3?依次输入每条边依附的两个节点，如果是网，则还需要输入该边的权值。

如果是无向图，则输入?a?b,查询节点 a、b?在节点数组?Vex[]?中存储下标?i、j，创建一个新的邻接点?s，让?s.v = j;s.next=null;然后将节点 s?插入第?i?个节点的第 1 个邻接点之前（头插法）。在无向图中，从节点 a 到节点 b 有边，从节点 b 到节点 a 也有边，因此还需要创建一个新的邻接点 s2，让 s2.v = i;s2.next=null;然后让?s2?节点插入第?j?个节点的第 1 个邻接点之前（头插法）。
如果是无向图，则输入?a?b,查询节点 a、b?在节点数组?Vex[]?中存储下标?i、j，创建一个新的邻接点?s，让?s.v = j;s.next=null;然后将节点 s?插入第?i?个节点的第 1 个邻接点之前（头插法）。
如果是无向网或有向网，则和无向图或有向图的处理方式一样，只是邻节点多了一个权值域。

四?实现

package graph;

import java.util.Scanner;

public class CreateALGraph {
    static final int MaxVnum = 100;  // 顶点数最大值

    public static void main(String[] args) {
        ALGraph G = new ALGraph();
        for (int i = 0; i < G.Vex.length; i++) {
            G.Vex[i] = new VexNode();
        }
        CreateALGraph(G); // 创建有向图邻接表
        printg(G); // 输出邻接表
    }

    static int locatevex(ALGraph G, char x) {
        for (int i = 0; i < G.vexnum; i++) // 查找顶点信息的下标
            if (x == G.Vex[i].data)
                return i;
        return -1; // 没找到
    }

    // 插入一条边
    static void insertedge(ALGraph G, int i, int j) {
        AdjNode s = new AdjNode();
        s.v = j;
        s.next = G.Vex[i].first;
        G.Vex[i].first = s;
    }

    // 输出邻接表
    static void printg(ALGraph G) {
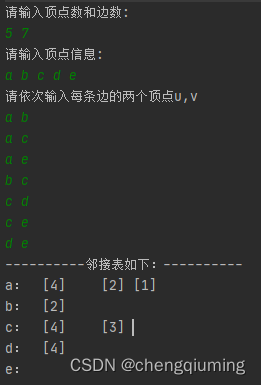
        System.out.println("----------邻接表如下：----------");

        for (int i = 0; i < G.vexnum; i++) {
            AdjNode t = G.Vex[i].first;
            System.out.print(G.Vex[i].data + "：  ");
            while (t != null) {
                System.out.print("[" + t.v + "]\t");
                t = t.next;
            }
            System.out.println();
        }
    }

    // 创建有向图邻接表
    static void CreateALGraph(ALGraph G) {
        int i, j;
        char u, v;

        System.out.println("请输入顶点数和边数:");
        Scanner scanner = new Scanner(System.in);
        G.vexnum = scanner.nextInt();
        G.edgenum = scanner.nextInt();
        System.out.println("请输入顶点信息:");

        for (i = 0; i < G.vexnum; i++)//输入顶点信息，存入顶点信息数组
            G.Vex[i].data = scanner.next().charAt(0);
        for (i = 0; i < G.vexnum; i++)
            G.Vex[i].first = null;
        System.out.println("请依次输入每条边的两个顶点u,v");

        while (G.edgenum-- > 0) {
            u = scanner.next().charAt(0);
            v = scanner.next().charAt(0);
            i = locatevex(G, u); // 查找顶点 u 的存储下标
            j = locatevex(G, v); // 查找顶点 v 的存储下标
            if (i != -1 && j != -1)
                insertedge(G, i, j);
            else {
                System.out.println("输入顶点信息错！请重新输入！");
                G.edgenum++; // 本次输入不算
            }
        }
    }
}

// 定义邻接点类型
class AdjNode {
    int v; // 邻接点下标
    AdjNode next; // 指向下一个邻接点
}

// 定义顶点类型
class VexNode {
    char data; // VexType为顶点的数据类型，根据需要定义
    AdjNode first; // 指向第一个邻接点
}

// 定义邻接表类型
class ALGraph {
    VexNode Vex[] = new VexNode[CreateALGraph.MaxVnum];
    int vexnum; // 顶点数
    int edgenum; // 边数
}