目录
一.柱状图中的最大矩形问题
1.题目
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例:
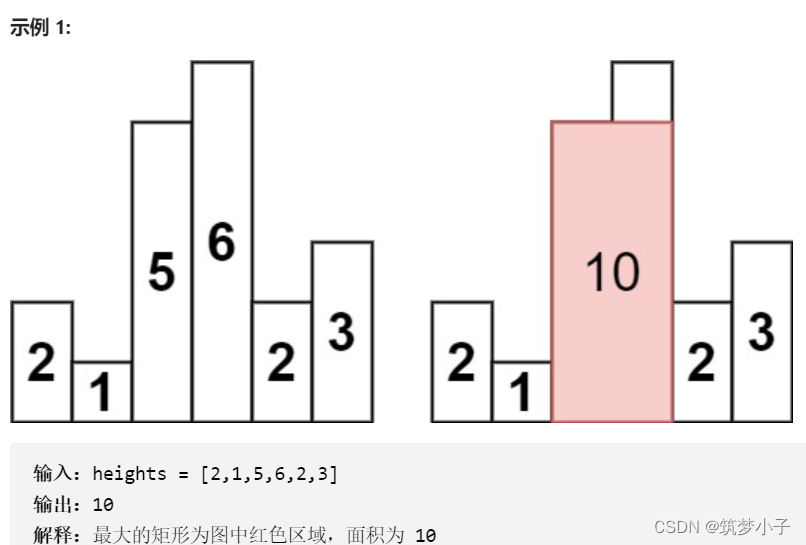
?
?
2.思路图解
首先初始化一个辅助数组,大小比当前数组大2,目的是为了处理左右边界,防止在左右边界出现最大值;借助栈实现,栈中存储的是元素的下标,如果当前元素比栈顶元素大,就出栈(保证栈不为空),这时候出栈元素就是矩形的高,新的栈顶就是左边界,有边界就是当前元素的下标;
确定好左右边界后,然后就计算当前矩阵的面积,与最大面积进行比较,如果比最大面积大,就修改,直到所有元素处理完,返回结果。
由于栈是单调递增的,当不满足单调递增时,就说明前一个元素可以确定矩形的面积了,如果加入当前元素后满足单调递增,说明还不能够确定栈顶元素的矩形面积。

?
?
3.代码
public int largestRectangleArea(int[] heights) {
//存储当前元素的索引
Deque<Integer> stack = new ArrayDeque<>();
int[] newheights = new int[heights.length+2];
for(int i=1; i<=heights.length; i++) {
newheights[i] = heights[i-1];
}
int res = 0;
for(int i=0; i<newheights.length; i++) {
while(!stack.isEmpty() && newheights[i]<newheights[stack.peek()]) {
//说明栈顶元素比当前元素大,弹出栈顶元素
int index = stack.pop();
int left = stack.peek();//栈顶前一个元素为左边界
int right = i;//i位置为右边界
res = Math.max(res, (right-left-1)*newheights[index]);
}
stack.push(i);
}
return res;
}?
?
二.最大矩形
1.题目
给定一个仅包含?0?和?1?、大小为?rows x cols?的二维二进制矩阵,找出只包含?1?的最大矩形,并返回其面积。
示例:
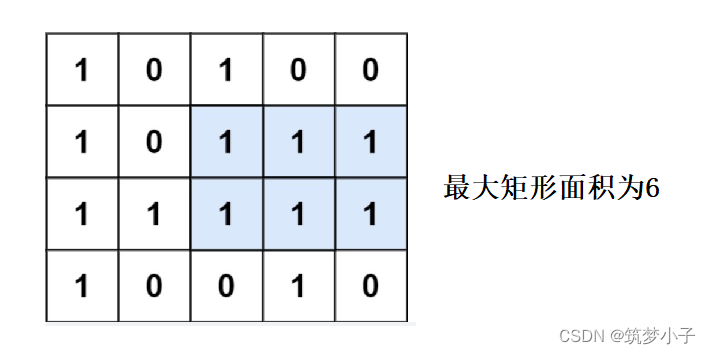
?
?
2.思路图解
(1)方法一(枚举求解)
首先初始化当前元素在当前行的宽度,初始化宽度;然后向上找高度,在找的时候宽度也要发生变化,为当前位置和之前结果的最小值,然后计算当前位置的矩形面积,如果大于之前的结果,就保存当前结果。
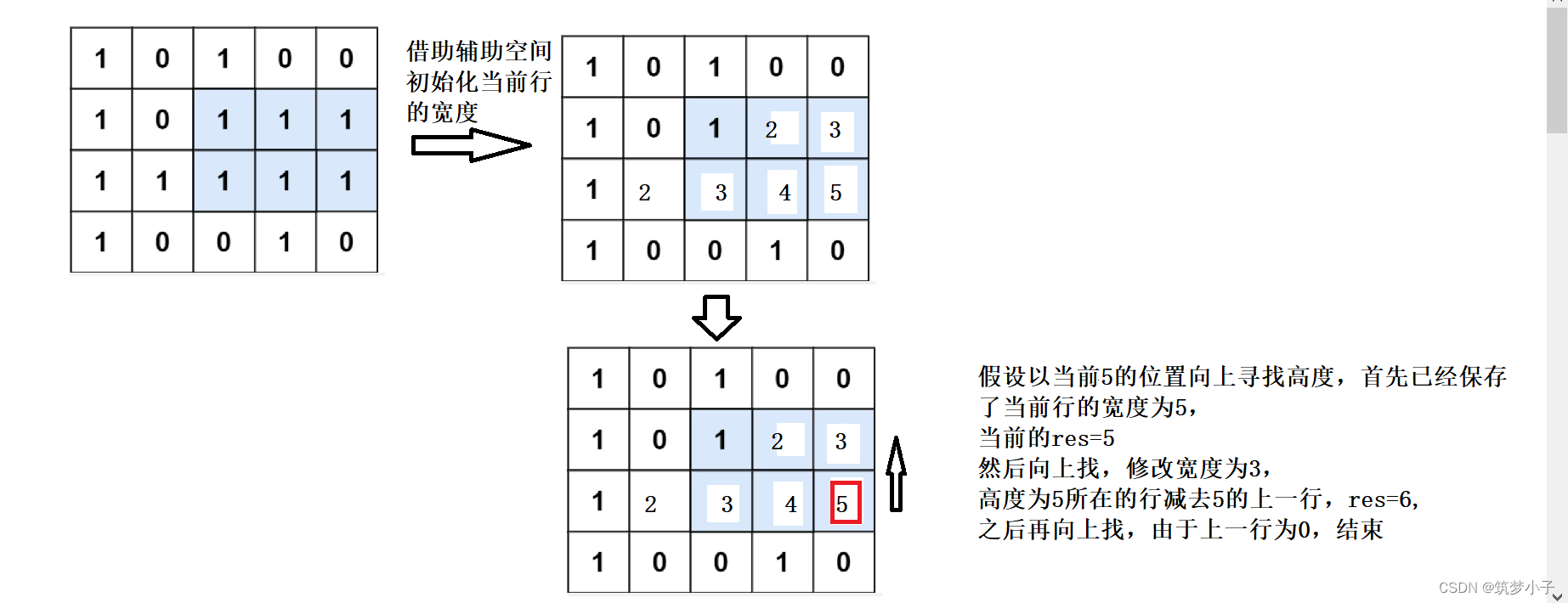
?
(2)方法二(单调栈)
单调栈的步骤如题目一所示
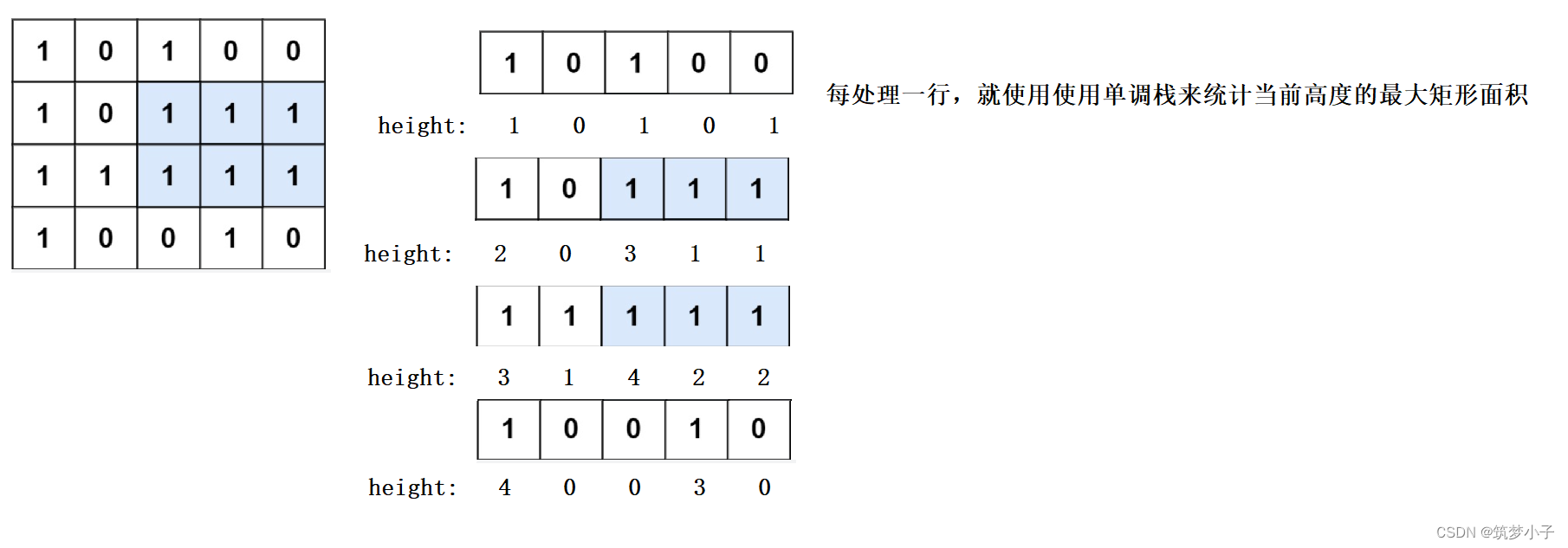
?
?
3.代码
方式一(枚举宽和高来求解)
//计算最大矩形
public int maximalRectangle(char[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int[][] mat = new int[m][n];//保存矩形的长宽
int res = 0;
for (int row = 0; row < m; row++) {
for (int col = 0; col < n; col++) {
if (matrix[row][col] == '1') {
//第一列初始化为自身
if (col == 0) {
mat[row][col] = 1;
} else {
//就初始化为当前行的前一列的数加1(相当于统计宽度)
mat[row][col] = mat[row][col - 1] + 1;
}
}
//保存高为1的宽度
int minWidth = mat[row][col];
//向上增加高度,每次的高度变化时,宽度也要保存当前高度下的最小值
for (int rowUp = row; rowUp >= 0; rowUp--) {
int height = row - rowUp + 1;
minWidth = Math.min(minWidth, mat[rowUp][col]);
res = Math.max(res, minWidth * height);
}
}
}
return res;
}方法二(柱状图的思路,使用单调栈求解)
public int maximalRectangle(char[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int[] heights = new int[n];
int res = 0;
for(int i=0; i<m; i++) {
for (int j=0; j<n; j++) {
//统计当前行的高度()
if(matrix[i][j] == '1') {
//说明有高度,并加上一行的高度
heights[j]+=1;
}else {
//说明没有高度,就将高度置为空
heights[j] = 0;
}
}
//根据单调栈进行求解
res = Math.max(res, maxReectangle(heights));
}
return res;
}
public int maxReectangle(int[] heights) {
int[] height = new int[heights.length+2];
Deque<Integer> stack = new ArrayDeque<>();
int res = 0;
//初始化一个新数组,方便处理边界问题
for(int i=1; i<=heights.length; i++) {
height[i] = heights[i-1];
}
for(int i=0; i<height.length; i++) {
//构造单调递增栈,如果非递增,就说明可以确定前面一个矩形的面积
while(!stack.isEmpty() && height[i]<height[stack.peek()]) {
//当前高度的下标
int idx = stack.pop();
//左边界的下标
int left = stack.peek();
//右边界的下标
int right = i;
res = Math.max(res, (right-left-1)*height[idx]);
}
stack.push(i);
}
return res;
}