一、 B树
1、B树的概念
B树是一种绝对平衡的多路查找树,B树中所有节点的子树个数最大值称为B树的阶,用m表示。一颗m阶的B树如果不为null,就必须满足一下性质:
- 树中每个节点之多有
m-1个关键字,即最多有m棵子树。 - 除了根节点以外,所有非叶子节点至少含有
[m/2]-1个关键字,所以最少有[m-2]棵子树。(叶结点全为null)。 - 根结点关键字可以小于
[m/2]-1,可以没有子树,若有子树则至少为2个,因为B树是绝对平衡树,高度差为0。 - 非叶结点结构为:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1NTkptFU-1655360655348)(C:\Users\ZhaLeMaoDeMao\AppData\Roaming\Typora\typora-user-images\image-20220615105523125.png)]
k代表关键字,并且k1 < k2 < k3 ······< kn
p代表关键字两边指向的子树。
问题 n个关键字的m阶B树:
1、有多少个叶节点
n+1
2、最小高度是多少
最胖的树最小,即每个结点都满足最大关键字m-1
m^h
高度 最大结点数 最大关键字总数 1 1 5 1 5^1 51 -1 2 5 5 2 5^2 52 -1 3 25 5 3 5^3 53 -1 h m h m^h mh m h m^h mh-1 所以 最小高度为 m h m^h mh-1 >= n
即
h >= $\log_m (n+1)$
3、最大高度是多少
最瘦的树最大,即每个结点都蛮子最小关键字数
[m/2]-1,每层满足最小结点数[m/2],设最小结点数为k,则关键字数为k-1.
高度 最小结点数 最小关键字数 1 1 1 2 2 5=4+1 3 6 17=12+4+1 h 2 k h ? 2 k^{h-2} kh?2 2 k h ? 2 k^{h-2} kh?2(k-1)
所以h高度的关键字数目为1+2( k 0 k^0 k0+ k 1 k^1 k1+ k 2 k^2 k2········ k h ? 2 k^{h-2} kh?2 )*(k-1)<= n
化简得:1+2( k h ? 1 k^{h-1} kh?1 -1)<=n
h <= $\log_k\frac{n+1}{2}$+1
2、B树的插入
主要在于分裂的过程,若不需要分裂直接放入即可。
分裂方法:
? 1、从中间位置也就是
[m/2]的位置分裂,将关键字分为两部分,左边的关键字不动还在原结点,右边的关键字放在同一层新的结点,中间位置插入到原结点父结点中。? 2、如果上一步执行完之后,
父节点也超出了关键字的上限,则对父结点进行分裂,直到传到根节点,如果根节点也超过限制,根结点继续分裂,产生新的根结点,树的高度加一。
演示插入过程: 首先,声明一个五阶B树
一、插入30、40、20、60
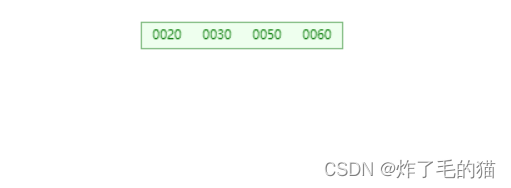
二、继续插入40,这时需要分裂,先按照上述分裂方法1执行,然后执行分裂方法2,产生新的根节点
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fb1ky8Dx-1655360655353)(C:\Users\ZhaLeMaoDeMao\AppData\Roaming\Typora\typora-user-images\image-20220616141341872.png)]](https://img-blog.csdnimg.cn/ecd7ef092eed4b1da1da4c107e9aae2d.png)
三、继续插入23、28
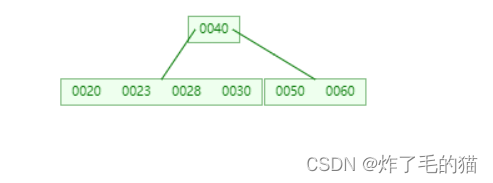
四、继续插入25,发生分裂,按照分裂方法1。
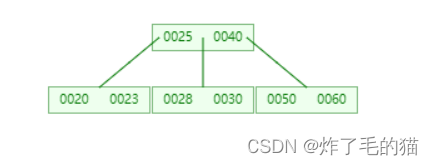
五、继续插入22、24、26、29
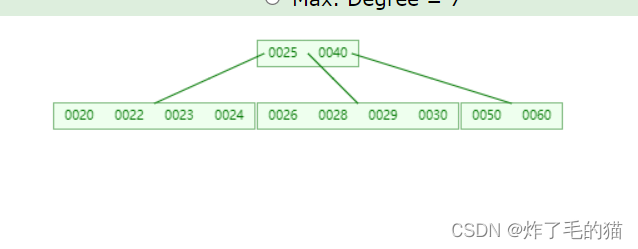
六、继续插入21、27、这时根节点关键字已经达到最大值
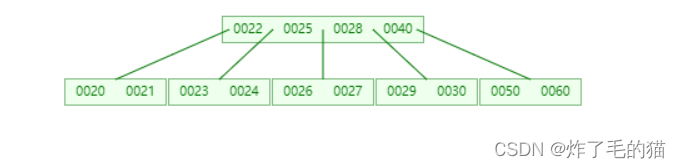
七、继续插入55、70
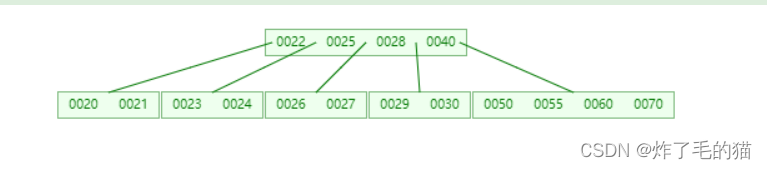
八、继续插入80,此时最右边子树发生分裂,60移动到父结点位置,但父结点位置已经达到最大值,再次分裂产生新的根节点。
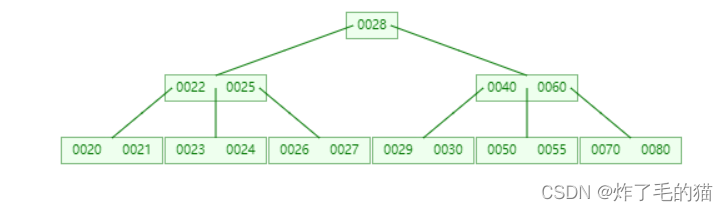
3、B树的删除
1、若B树被删除的结点位于终端节点,并且该结点的关键字数
大于[m/2]-1,则直接删除即可。2、若B树被删除的结点位于终端结点,但该节点关键字数
等于[m/2]-1,则向兄弟结点(左或右)结点关键字大于[m/2]-1的结点借一个关键字,但并是直接借而是拿父结点的结点,有以下三种情况? 2.1、被删除结点的关键字
均比父结点小,则只有右兄弟,将父结点最小的关键字放到该位置,右兄弟最小的关键字放到父结点。? 2.2、被删除结点的关键字
均比父节点大,则只有左兄弟,将父结点最大的关键字放到该位置,左兄弟最大的关键字放到父结点。? 2.3、被删除结点的关键字位于
父结点的中间,即有右兄弟,又有左兄弟,如果向右兄弟借,其实就是2.1;若向左兄弟借,其实就是2.2。3、若B树被删除的结点位于终端结点,并且该结点关键字个数等于
[m/2]-1,而与该结点相邻的兄弟结点关键字也等于[m/2]-1,把当前结点和相邻结点再加上父结点中关键字(分割关键字)进行合并。如果合并导致父结点关键字小于[m/2]-1,则以父结点向上遍历,直到根节点。4、如果待删除的关键字不在终端结点,则用该关键字的
直接前驱或者直接后继代替关键字,直到终端结点,把问题转化为终端节点。? 直接前驱:当前关键字
左侧结点最右边的关键字。? 直接后继:当前关键字
右侧结点最左边的关键字。
演示过程: B树如下图所示:
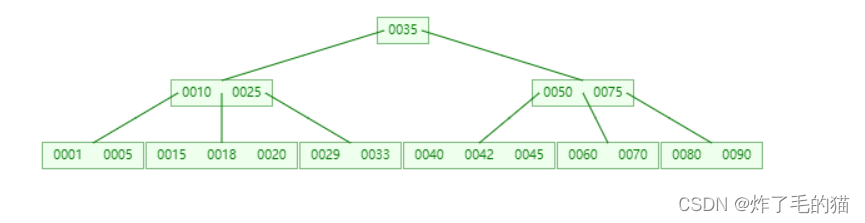
一、删除42,符合情形 1 ,直接删除
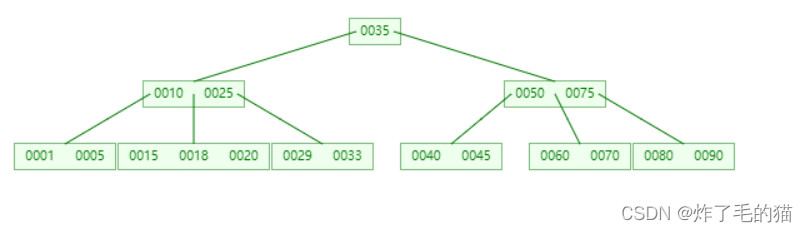
二、删除33,符合情形 2
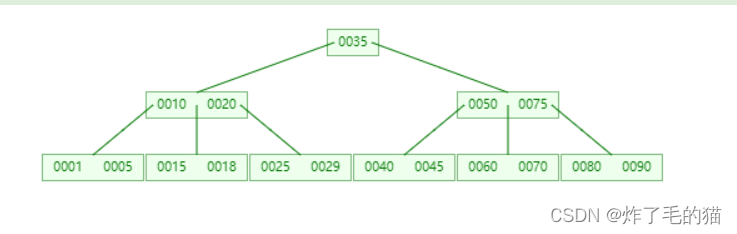
三、删除29,符合情形 3
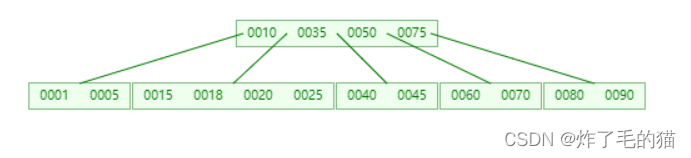
四、删除35,对应情形 4
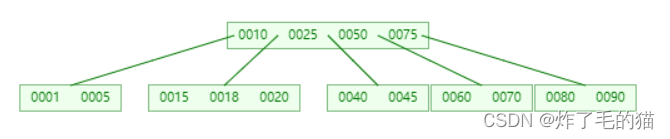
五、删除40,对应情形 2,分割节点下移,左兄结点最大值上移
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B2RP1A9o-1655446089821)(C:\Users\ZhaLeMaoDeMao\AppData\Roaming\Typora\typora-user-images\image-20220617140607796.png)]](https://img-blog.csdnimg.cn/799af5473974442ca410e3d231781848.png)
二、B+树
1、B+树的概念
B+树与B树非常相似,先看相同点:
-
根结点至少一个元素
-
非根节点范围:[m/2] <= k < = m-1
不同点:
- B+树的
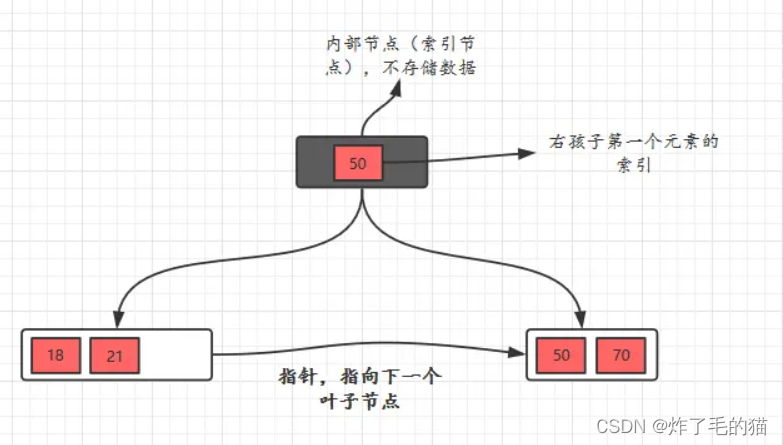
只有叶子结点存储数据,非叶子结点不存储数据,这是与B树最大的不同。 - 内部结点中的key都按照从小到大的顺序排列,对于内部结点中的一个key,左树中的所有key都小于它,右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。
- 每个叶子结点都存有相邻叶子结点的指针,叶子结点本身依关键字的大小自小而大顺序链接。
- 父节点存有右孩子的第一个元素的索引。
2、B+树的插入
? B+树与B树的插入很相似,不同点是
当节点元素数量大于
m-1的时候,按中间元素分裂成左右两部分,中间元素分裂到父节点当做索引存储,但是,本身中间元素还是分裂右边这一部分的,叶子结点通过指针连接起来。
演示插入过程:首先声明一个5阶B+树
一、依次插入 10、20、30、40

二、插入 50 ,发生分裂
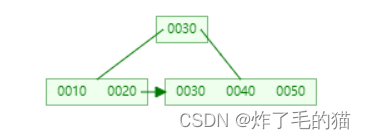
三、继续插入45、60,发生分裂
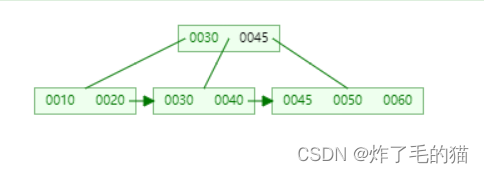
3、B+树的删除
与上面B树类似,有些许的不同。
1、结点个数大于[m/2]直接删除,如果父结点关键字指向被删除关键字所在结点,更新父结点索引。
2、被删除结点个数
等于[m/2],兄弟节点的元素大于[m/2],叶子节点有指针的存在,向兄弟节点借元素时,不需要通过父节点了,而是可以直接通过兄弟节点移动即可,然后更新父节点的索引。3、被删除结点个数等于[m/2],并且兄弟结点元素不大于[m/2],则将当前节点和兄弟节点合并,然后更新父节点的索引。
示例:声明一个5阶B+树
一、初始如图所示
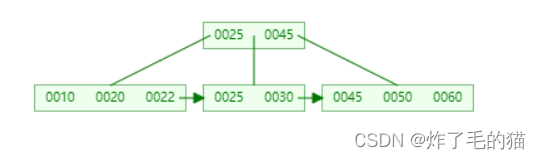
二、删除60,直接删除即可
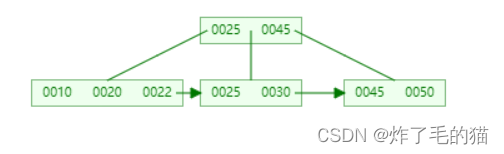
三、删除45,需要合并,并更新父结点关键字(其实这儿是被删除了)
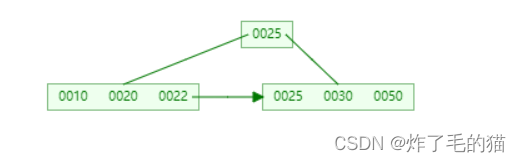
四、删除25
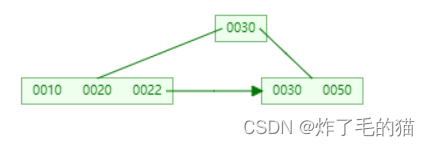
总结
B+树相对于B树有一些自己的优势,可以归结为下面几点。
- 单一节点存储的元素更多,使得查询的IO次数更少,所以也就使得它更适合做为数据库MySQL的底层数据结构了。
- 所有的查询都要查找到叶子节点,查询性能是稳定的,而B树,每个节点都可以查找到数据,所以不稳定。
- 所有的叶子节点形成了一个有序链表,更加便于查找。