[数据结构与算法] lc marathon 2022.6.22

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> lc marathon 2022.6.22 -> 正文阅读

[数据结构与算法]lc marathon 2022.6.22

文章目录

剑指 Offer 55 - I. 二叉树的深度

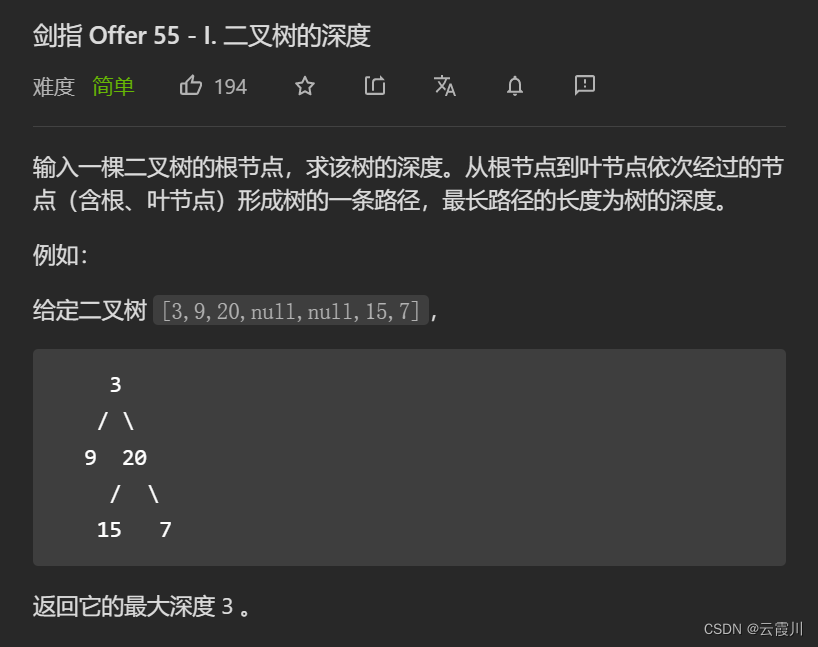
在这里插入图片描述

计算树的深度

对于每个节点；

max（左子树高度，右子树高度）+ 1

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        """
        用遍历即可
        """
        return dfs(root)
def dfs(root):
    if root==None:
        return 0
    l1=dfs(root.left)
    l2=dfs(root.right)
    return 1+max(l1,l2)

在这里插入图片描述

剑指 Offer 56 - I. 数组中数字出现的次数

在这里插入图片描述

这道题是一个升级版，简单版本只有一个数出现了一次，其他数都出现了两次。

运用位运算即可，相同的数异或会为0，不同的数异或不为0，0和某数异或该数不变且满足交换律

因此把数组中所有数全部异或，即得到该数

对于该题

相同的数异或为0，不同的异或为1。0和任何数异或等于这个数本身。

所以，数组里面所有数异或 = 目标两个数异或。由于这两个数不同，所以异或结果必然不为0。

假设数组异或的二进制结果为10010，那么说明这两个数从右向左数第2位是不同的

那么可以根据数组里面所有数的第二位为0或者1将数组划分为2个。

这样做可以将目标数必然分散在不同的数组中，而且相同的数必然落在同一个数组中。

这两个数组里面的数各自进行异或，得到的结果就是答案

class Solution:
    def singleNumbers(self, nums: List[int]) -> List[int]:
        l=0
        for num in nums:
            l=l^num
        s=bin(l)
        j=0
        s=s.split('0b')[1]
        for i in range(-1,-len(s)-1,-1):
            if s[i]=='1':
                j=i
                break
        l1=0
        l2=0
        for num in nums:
            num_str=bin(num).split('0b')[1]
            if abs(j)>len(num_str) or num_str[j]=='0':
                l1=l1^num
            else:
                l2=l2^num

        return [l1,l2]

在这里插入图片描述

剑指 Offer 56 - II. 数组中数字出现的次数 II

这题没要求，直接用字典
在这里插入图片描述

from collections import Counter
class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        dic=Counter(nums)
        for num in dic.keys():
            if dic[num]==1:
                return num
        return -1

在这里插入图片描述

python不同进制转换tips

# 十进制转二进制
bin(3)  -->  0b11  str
# 二级制转10进制
int("11" or "0b11" or 11,2)  --> 3 int 
同理 八进制 十六进制

剑指 Offer 57. 和为s的两个数字

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        s=set()
        for num in nums:
            if target-num in s:
                return [num,target-num]
            s.add(num)
        return -1