B树
它是一种平衡的多叉树,称为B树。
一棵M阶(M>2)的B树,是一棵平衡的M路平衡搜索树。
B树的实现:
public class BTreeNode {
//一个B-树节点中,能存的key的数量的上限
public static final int KEY_LIMIT = 4;
//KEY_LIMIT+1:是因为插入空间已满不会进行分裂,再插入一个key使得>4的时候才会进行分裂
public long[] keyList = new long[KEY_LIMIT+1];
//记录目前拥有的key的个数
public int size = 0;
//区间范围
public BTreeNode[] childList = new BTreeNode[KEY_LIMIT+2];
public BTreeNode parent = null;
@Override
public String toString() {
return String.format("%d: %s", size, Arrays.toString(Arrays.copyOf(keyList, size)));
}
/**
* 查找key位于哪一个子树中
*/
public BTreeNode findKey(long key) {
if (key > keyList[size-1]) {//最后一个数
return childList[size];
}
for (int i = 0; i < size; i++) {
if (key == keyList[i]) {
return this;
} else if (key < keyList[i]) {
//第一个大于key的关键字元素
return childList[i];
}
}
return null;
}
public InsertResult insertKeyWithChild(long key, BTreeNode node) {
// 1. 让 key 按序插入到 keyList 中
int index = insertIntoKeyList(key);
// 2. 根据 index 进行 child 的插入
// childList[0, size]
// [0, index] 不动
// [index + 1]位置 要插入 node 的下标
// [index + 1, size] 搬到 [index + 2, size + 1] 元素个数 == size - index
System.arraycopy(childList,index+1,childList,index+2,size-index);
childList[index+1] = node;
size++;
// 2. 判断是否需要进行分裂
// 3. 如果有必要,进行结点分裂
if (shouldSplit()) {
return splitNotLeaf();
}
return null;
}
//非叶子节点的分裂
private InsertResult splitNotLeaf() {
int size = this.size;
//1.找到中间位置
int index = size / 2;
//2.保存要分裂出的key
InsertResult result = new InsertResult();
result.key = keyList[index];
/**
* 3. 处理 key 的分裂
* 哪些 key 应该留在当前结点中 [0,index) 一共index个
* 哪个 key 是分裂出的 key [index]
* 哪些 key 应该在新结点中 (index,size) 一共size-index-1个
*/
//将(index,size)位置上的key搬到新节点中
BTreeNode node = new BTreeNode();//创建新节点
System.arraycopy(keyList,index+1,node.keyList,0,size-index-1);
node.size = size-index-1;
//把 [index,size)所有的key重置为0,重置size
Arrays.fill(keyList,index,size,0);
this.size = index;
//4.对非叶子节点进行分裂
System.arraycopy(this.childList, index + 1, node.childList, 0, size - index);
//[index + 1, size + 1)
Arrays.fill(this.childList, index + 1, size + 1, null);
for (int i = 0; i < size - index; i++) {
node.childList[i].parent = node;
}
/**
* 5.处理分裂的parent问题
* 1)this.parent不变,分裂不影响父子关系
* 2)node.parent和this是同一父亲
*/
node.parent = this.parent;
result.node = node;
return result;
}
public static class InsertResult{
public long key; //分裂出的key
public BTreeNode node;//分裂出的新节点
}
public InsertResult insertKey(long key) {
//key 按序插入到 keyList 中
insertIntoKeyList(key);
size++;
//判断是否要进行分裂
if (shouldSplit( )) {
return splitLeaf();
}
return null;
}
//节点分裂
private InsertResult splitLeaf() {
int size = this.size;
//1.找到中间位置
int index = size / 2;
//2.保存要分裂出的key
InsertResult result = new InsertResult();
result.key = keyList[index];
/**
* 3. 处理 key 的分裂
* 哪些 key 应该留在当前结点中 [0,index) 一共index个
* 哪个 key 是分裂出的 key [index]
* 哪些 key 应该在新结点中 (index,size) 一共size-index-1个
*/
//将(index,size)位置上的key搬到新节点中
BTreeNode node = new BTreeNode();//创建新节点
System.arraycopy(keyList,index+1,node.keyList,0,size-index-1);
node.size = size-index-1;
//把 [index,size)所有的key重置为0,重置size
Arrays.fill(keyList,index,size,0);
this.size = index;
//4.对叶子节点进行分裂,如果childList == null,则不需要分裂
/**
* 5.处理分裂的parent问题
* 1)this.parent不变,分裂不影响父子关系
* 2)node.parent和this是同一父亲
*/
node.parent = this.parent;
result.node = node;
return result;
}
//判断是否要进行分裂
private boolean shouldSplit() {
return size > KEY_LIMIT;
}
//key 按序插入到 keyList 中
private int insertIntoKeyList(long key) {
int i;
for (i = size-1; i >= 0; i--) {
if (keyList[i] < key) {
break;
}
//将值往后移动一格,继续查找
keyList[i+1] = keyList[i];
}
keyList[i+1] = key;
return i+1;
}
}
public class BTree {
//B-树的根节点
public BTreeNode root = null;
//B-树中key的个数
public int size = 0;
public boolean insert(long key) {
if (insertWithoutSize(key)) {
size++;
return true;
}
return false;
}
private boolean insertWithoutSize(long key) {
//判定是否是空树
if(root == null) {
root = new BTreeNode();
root.keyList[0] = key;
root.size = 1;
return true;
}
//不是空树
BTreeNode cur = root;
while (true) {
BTreeNode node = cur.findKey(key);
if (node == cur) {
//key就在cur节点中
//不能重复插入
return false;
} else if (node == null) {
//cur就是叶子节点,直接插入
break;
} else {
//找到一个孩子,而且cur不是叶子
cur = node;
}
}
//进行key的插入
BTreeNode.InsertResult result = cur.insertKey(key);
while (true) {
if (result == null) {
//插入中没有发生节点分裂
return true;
}
//说明发生了分裂
//需要把分裂出key和新节点插入相应的节点
BTreeNode parent = cur.parent;
if (parent == null) {
//cur是根节点
//根结点发生分裂了
// 需要一个新的根结点,来保存分裂出的 key
root = new BTreeNode();
root.keyList[0] = result.key;
root.size = 1;
root.childList[0] = cur;
root.childList[1] = result.node;
// 由于原来 current 是根结点,所以其 parent == null
// 自然分裂出的结点,跟着也是 null
// 所以为他们设置新的父结点
cur.parent = result.node.parent = root;
return true;
}
//不是根节点插入
result = parent.insertKeyWithChild(result.key,result.node);
cur = parent;
}
}
}
B+树
B+树的搜索与B-树基本相同,区别是B+树只有达到叶子节点才能命中(B-树可以在非叶子节点中命中)。
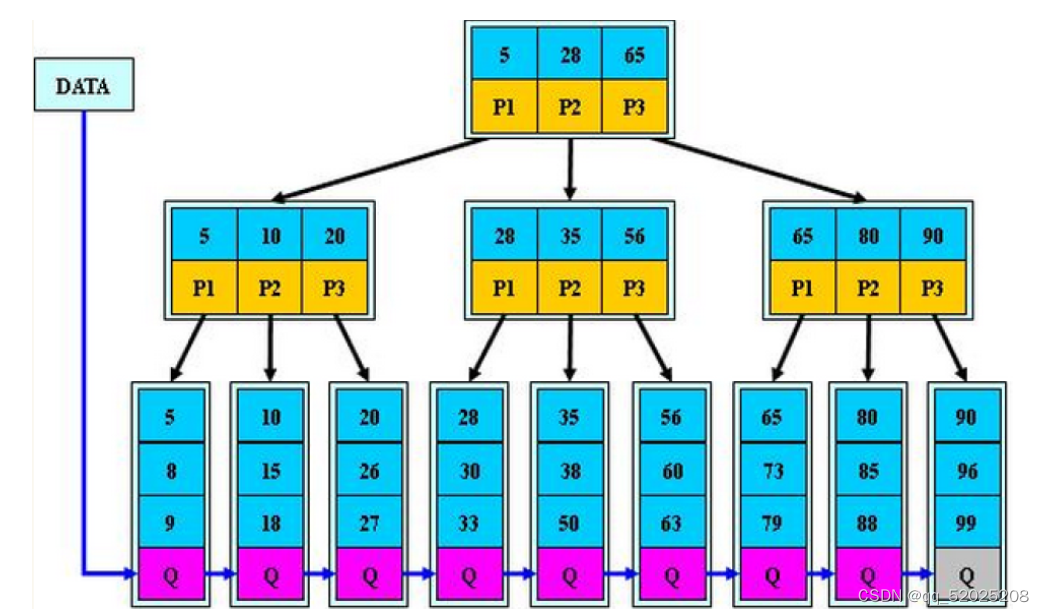
key一定都在叶子中保存一份。叶子节点通过链式结构关联。
数据库中常需要全key的扫描。
B+树的特性:
(1)所有关键字都出现在叶子节点的链表中(稠密索引),且链表中的节点都是有序的。
(2)不可能在非叶子节点中命中。
(3) 非叶子节点相当于是叶子节点的索引(稀疏索引),叶子节点相当于是存储数据的数据层。
(4)更适合文件索引系统
B+树与B-树的区别:
B-树:多路搜索树,每个结点存储M/2到M个关键字,非叶子节点存储指向关键字范围的节点;所有关键字在整棵树中出现,且只出现了一次,非叶子节点可以命中;
B+树:在B-树的基础上,为叶子节点增加链表指针,所有关键字都在叶子节点中出现,非叶子节点作为叶子节点的索引;B+树总是到叶子节点才可以命中。