8 输出反馈工作模式
8.1 变量定义
OFB工作模式采用以下变量。
a)输入变量:
??????1) q q q个明文分组 P 1 , P 2 , . . . , P q P_1,P_2,...,P_q P1?,P2?,...,Pq?所组成的序列,每个分组都为 j j j比特;
??????2)密钥 K K K,需要加解密操作方约定一致,长度由分组密码算法 E E E决定;
??????3)初始向量 I V IV IV,需要加解密操作方约定一致,长度为 n n n比特。
b)中间变量:
??????1) q q q个密码输入变量 X 1 , X 2 , . . . , X q X_1,X_2,...,X_q X1?,X2?,...,Xq?所组成的序列,每个变量都为 n n n比特;
??????2) q q q个密码输出变量 Y 1 , Y 2 , . . . , Y q Y_1,Y_2,...,Y_q Y1?,Y2?,...,Yq?所组成的序列,每个变量都为 n n n比特;
??????3) q q q个临时变量 Z 1 , Z 2 , . . . , Z q Z_1,Z_2,...,Z_q Z1?,Z2?,...,Zq?所组成的序列,每个变量都为 j j j比特。
c)输出变量:
q q q个密文分组 C 1 , C 2 , . . . , C q C_1,C_2,...,C_q C1?,C2?,...,Cq?所组成的序列,每个分组都为 j j j比特。
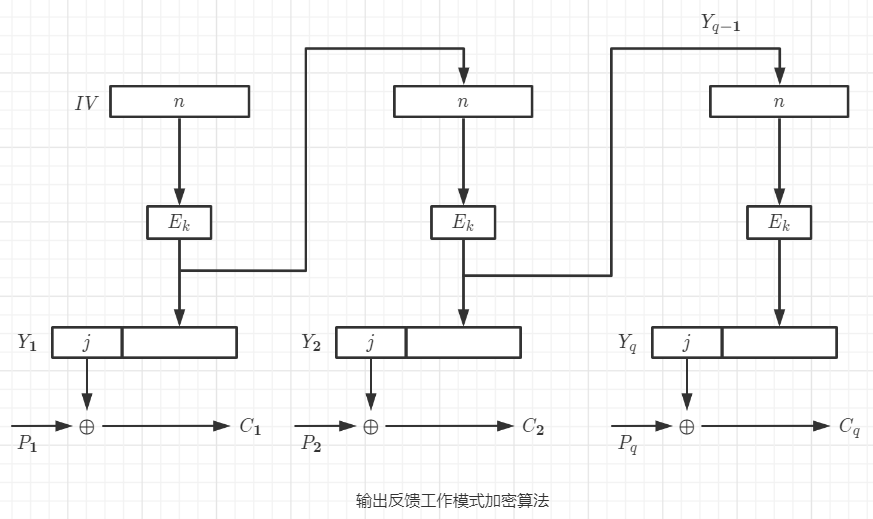
8.2 OFB的加密方式描述
设置密码输入变量 X X X的初始向量: X 1 = I V X_1=IV X1?=IV。
加密运算按照如下四个步骤进行:
a)使用分组密码: Y i = E k ( X i ) Y_i=E_k(X_i) Yi?=Ek?(Xi?);
b)选择左侧的 j j j比特: Z i = j ~ Y i Z_i=j \sim Y_i Zi?=j~Yi?;
c)生成密文分组: C i = P i ⊕ Z i C_i=P_i \oplus Z_i Ci?=Pi?⊕Zi?;
d)反馈操作: X i + 1 = Y i X_{i+1}=Y_i Xi+1?=Yi?。
对 i = 1 , 2 , . . . , q i=1,2,...,q i=1,2,...,q,重复上述步骤,最后一个循环结束于c)。此过程如下图所示。每次使用分组密码所生成的结果 Y i Y_i Yi?被用来反馈并成为 X X X的下一个值,即 X i + 1 X_{i+1} Xi+1?。 Y i Y_i Yi?的左侧 j j j比特用来加密明文分组。
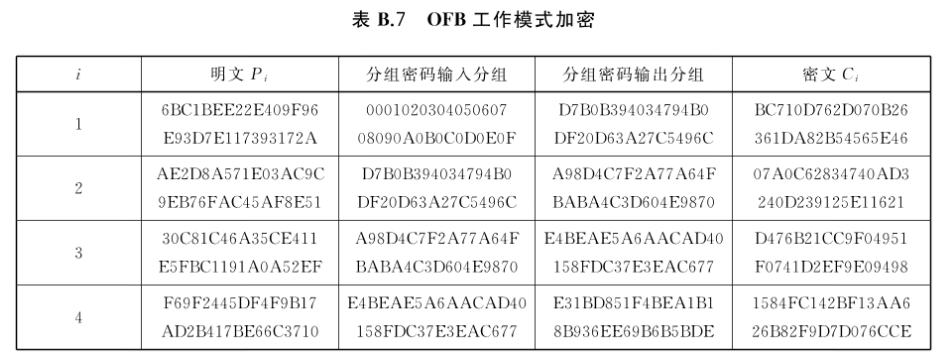
8.3 OFB的加密方式示例
本示例使用的分组密码是GB/T 32907——2016中规定的SM4算法。所有变量采用“左高右低”的方式标记,即变量最左侧为其最高位。
此例所选的参数为: j = 128 j=128 j=128。
密钥密钥为(十六进制):2B7E1516 28AED2A6 ABF71588 09CF4F3C。
初始向量为(十六进制):00010203 04050607 08090A0B 0C0D0E0F。
明文是(十六进制):6BC1BEE2 2E409F96 E93D7E11 7393172A
????????????????????????????????????AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
????????????????????????????????????30C81C46 A35CE411 E5FBC119 1A0A52EF
????????????????????????????????????F69F2445 DF4F9B17 AD2B417B E66C3710。
i = 1 i=1 i=1时:
X 1 = I V = X_1=IV= X1?=IV= 00010203 04050607 08090A0B 0C0D0E0F
a) Y 1 = E k ( X 1 ) = Y_1=E_k(X_1)= Y1?=Ek?(X1?)= D7B0B394 034794B0 DF20D63A 27C5496C
b) Z 1 = 128 ~ Y 1 = Z_1=128 \sim Y_1= Z1?=128~Y1?= D7B0B394 034794B0 DF20D63A 27C5496C
c) C 1 = P 1 ⊕ Z 1 = C_1=P_1 \oplus Z_1= C1?=P1?⊕Z1?= (6BC1BEE2 2E409F96 E93D7E11 7393172A) ⊕ \oplus ⊕ (D7B0B394 034794B0 DF20D63A 27C5496C) = BC710D76 2D070B26 361DA82B 54565E46
d) X 2 = Y 1 = X_2=Y_1= X2?=Y1?= D7B0B394 034794B0 DF20D63A 27C5496C
i = 2 i=2 i=2时:
a) Y 2 = E k ( X 2 ) = Y_2=E_k(X_2)= Y2?=Ek?(X2?)= A98D4C7F 2A77A64F BABA4C3D 604E9870
b) Z 2 = 128 ~ Y 2 = Z_2=128 \sim Y_2= Z2?=128~Y2?= A98D4C7F 2A77A64F BABA4C3D 604E9870
c) C 2 = P 2 ⊕ Z 2 = C_2=P_2 \oplus Z_2= C2?=P2?⊕Z2?= (AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51) ⊕ \oplus ⊕ (A98D4C7F 2A77A64F BABA4C3D 604E9870) = 07A0C628 34740AD3 240D2391 25E11621
d) X 3 = Y 2 = X_3=Y_2= X3?=Y2?= A98D4C7F 2A77A64F BABA4C3D 604E9870
i = 3 i=3 i=3时:
a) Y 3 = E k ( X 3 ) = Y_3=E_k(X_3)= Y3?=Ek?(X3?)= E4BEAE5A 6AACAD40 158FDC37 E3EAC677
b) Z 3 = 128 ~ Y 3 = Z_3=128 \sim Y_3= Z3?=128~Y3?= E4BEAE5A 6AACAD40 158FDC37 E3EAC677
c) C 3 = P 3 ⊕ Z 3 = C_3=P_3 \oplus Z_3= C3?=P3?⊕Z3?= (30C81C46 A35CE411 E5FBC119 1A0A52EF) ⊕ \oplus ⊕ (E4BEAE5A 6AACAD40 158FDC37 E3EAC677) = D476B21C C9F04951 F0741D2E F9E09498
d) X 4 = Y 3 = X_4=Y_3= X4?=Y3?= E4BEAE5A 6AACAD40 158FDC37 E3EAC677
i = 4 i=4 i=4时:
a) Y 4 = E k ( X 4 ) = Y_4=E_k(X_4)= Y4?=Ek?(X4?)= E31BD851 F4BEA1B1 8B936EE6 9B6B5BDE
b) Z 4 = 128 ~ Y 4 = Z_4=128 \sim Y_4= Z4?=128~Y4?= E31BD851 F4BEA1B1 8B936EE6 9B6B5BDE
c) C 4 = P 4 ⊕ Z 4 = C_4=P_4 \oplus Z_4= C4?=P4?⊕Z4?= (F69F2445 DF4F9B17 AD2B417B E66C3710) ⊕ \oplus ⊕ (E31BD851 F4BEA1B1 8B936EE6 9B6B5BDE) = 1584FC14 2BF13AA6 26B82F9D 7D076CCE
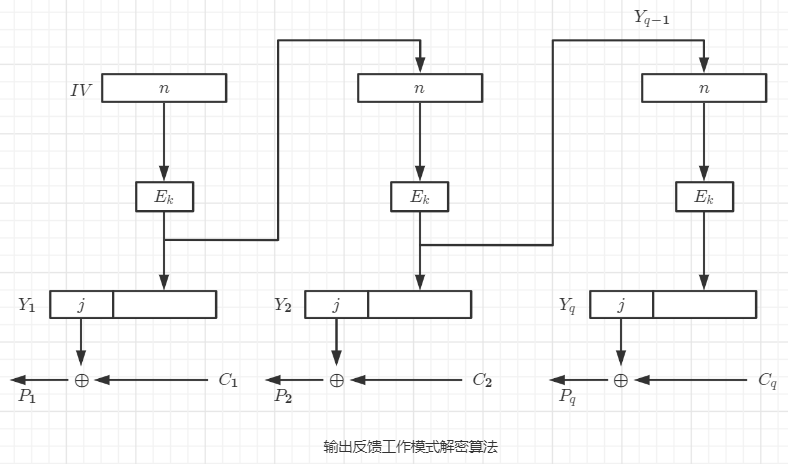
8.4 OFB的解密方式描述
设置密码输入变量 X X X的初始向量: X 1 = I V X_1=IV X1?=IV。
解密运算按照如下四个步骤进行:
a)使用分组密码: Y i = E k ( X i ) Y_i=E_k(X_i) Yi?=Ek?(Xi?);
b)选择左侧的 j j j比特: Z i = j ~ Y i Z_i=j \sim Y_i Zi?=j~Yi?;
c)生成明文分组: P i = C i ⊕ Z i P_i=C_i \oplus Z_i Pi?=Ci?⊕Zi?;
d)反馈操作: X i + 1 = Y i X_{i+1}=Y_i Xi+1?=Yi?。
对 i = 1 , 2 , . . . , q i=1,2,...,q i=1,2,...,q,重复上述步骤,最后一个循环结束于c)。此过程图下图所示。解密过程与加密过程仅在步骤c)有不同,相应的变量值 X i X_i Xi?和 Y i Y_i Yi?是相同的。
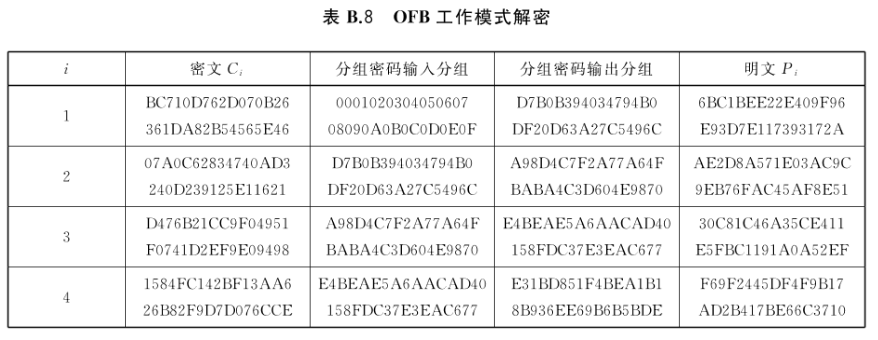
8.5 OFB的解密方式示例
本示例使用的分组密码是GB/T 32907——2016中规定的SM4算法。所有变量采用“左高右低”的方式标记,即变量最左侧为其最高位。
此例所选的参数为: j = 128 j=128 j=128。
密钥密钥为(十六进制):2B7E1516 28AED2A6 ABF71588 09CF4F3C。
初始向量为(十六进制):00010203 04050607 08090A0B 0C0D0E0F。
密文是(十六进制):BC710D76 2D070B26 361DA82B 54565E46
????????????????????????????????????07A0C628 34740AD3 240D2391 25E11621
????????????????????????????????????D476B21C C9F04951 F0741D2E F9E09498
????????????????????????????????????1584FC14 2BF13AA6 26B82F9D 7D076CCE。
i = 1 i=1 i=1时:
X 1 = I V = X_1=IV= X1?=IV= 00010203 04050607 08090A0B 0C0D0E0F
a) Y 1 = E k ( X 1 ) = Y_1=E_k(X_1)= Y1?=Ek?(X1?)= D7B0B394 034794B0 DF20D63A 27C5496C
b) Z 1 = 128 ~ Y 1 = Z_1=128 \sim Y_1= Z1?=128~Y1?= D7B0B394 034794B0 DF20D63A 27C5496C
c) P 1 = C 1 ⊕ Z 1 = P_1=C_1 \oplus Z_1= P1?=C1?⊕Z1?= (BC710D76 2D070B26 361DA82B 54565E46) ⊕ \oplus ⊕ (D7B0B394 034794B0 DF20D63A 27C5496C) = 6BC1BEE2 2E409F96 E93D7E11 7393172A
d) X 2 = Y 1 = X_2=Y_1= X2?=Y1?= D7B0B394 034794B0 DF20D63A 27C5496C
i = 2 i=2 i=2时:
a) Y 2 = E k ( X 2 ) = Y_2=E_k(X_2)= Y2?=Ek?(X2?)= A98D4C7F 2A77A64F BABA4C3D 604E9870
b) Z 2 = 128 ~ Y 2 = Z_2=128 \sim Y_2= Z2?=128~Y2?= A98D4C7F 2A77A64F BABA4C3D 604E9870
c) P 2 = C 2 ⊕ Z 2 = P_2=C_2 \oplus Z_2= P2?=C2?⊕Z2?= (07A0C628 34740AD3 240D2391 25E11621) ⊕ \oplus ⊕ (A98D4C7F 2A77A64F BABA4C3D 604E9870) = AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
d) X 3 = Y 2 = X_3=Y_2= X3?=Y2?= A98D4C7F 2A77A64F BABA4C3D 604E9870
i = 3 i=3 i=3时:
a) Y 3 = E k ( X 3 ) = Y_3=E_k(X_3)= Y3?=Ek?(X3?)= E4BEAE5A 6AACAD40 158FDC37 E3EAC677
b) Z 3 = 128 ~ Y 3 = Z_3=128 \sim Y_3= Z3?=128~Y3?= E4BEAE5A 6AACAD40 158FDC37 E3EAC677
c) P 3 = C 3 ⊕ Z 3 = P_3=C_3 \oplus Z_3= P3?=C3?⊕Z3?= (D476B21C C9F04951 F0741D2E F9E09498) ⊕ \oplus ⊕ (E4BEAE5A 6AACAD40 158FDC37 E3EAC677) = 30C81C46 A35CE411 E5FBC119 1A0A52EF
d) X 4 = Y 3 = X_4=Y_3= X4?=Y3?= E4BEAE5A 6AACAD40 158FDC37 E3EAC677
i = 4 i=4 i=4时:
a) Y 4 = E k ( X 4 ) = Y_4=E_k(X_4)= Y4?=Ek?(X4?)= E31BD851 F4BEA1B1 8B936EE6 9B6B5BDE
b) Z 4 = 128 ~ Y 4 = Z_4=128 \sim Y_4= Z4?=128~Y4?= E31BD851 F4BEA1B1 8B936EE6 9B6B5BDE
c) P 4 = C 4 ⊕ Z 4 = P_4=C_4 \oplus Z_4= P4?=C4?⊕Z4?= (1584FC14 2BF13AA6 26B82F9D 7D076CCE) ⊕ \oplus ⊕ (E31BD851 F4BEA1B1 8B936EE6 9B6B5BDE) = F69F2445 DF4F9B17 AD2B417B E66C3710
8.6 输出反馈工作模式的性质
8.6.1 场景
只要使用同样的密钥和初始向量对相同的明文进行加密,OFB模式将生成相同的密文。此外,当使用相同的密钥和 I V IV IV时,OFB模式中将会生成相同的密钥流,因此,为了保密起见,对于一个给定的密钥,一个特定的 I V IV IV只能使用一次。
8.6.2 性质
OFB模式的性质有:
a)没有链接操作会使得OFB模式容易受到主动的攻击;
b)使用不同的 I V IV IV值生成不同的密钥流,可防止同一明文加密成同一密文;
c)OFB模式的加密和解密过程都使用分组密码的加密运算;
d)OFB模式不依赖明文来生成用于对明文进行异或运算的密钥流;
e)加解密操作方需要约定一致的参数 j j j,参数的取值可公开;
f)对于每个明文,选择一个较小的 j j j值将需要更多次的分组密码操作,从而引起更大的处理开销。
8.6.3 填充明文
只有长度为 j j j比特倍数的明文才能被加密。其他长度的明文需要填充至 j j j比特的整数倍。但是,经常选择 j j j的大小使得明文无需进行填充,例如对于明文的最后部分可以修改 j j j。
8.6.4 差错控制
OFB模式中,密文中每一差错比特只会引起明文中同一位置出现一个差错比特,不影响明文其他位置。
8.6.5 同步
OFB模式不是自动同步的。如果加密和解密两个操作不同步,系统需要重新初始化。这种同步丢失可能由于插入或丢失任意数目的密文所引起。
每次重新初始化应使用一个新的 I V IV IV值,它不同于与同一个密钥一起使用的以前的 I V IV IV值。其原因是对于相同的参数,每次会生成相同的比特流,这将易于受到“已知明文攻击”。