[数据结构与算法]acwing 838. 堆排序 (手写一个堆)

如何手写一个堆？

1. 插入一个数
2. 求集合中最小值
3. 删除最小值
4. 删除任意一个元素
5. 修改任意一个元素
   [注]： 后面两个是stl 无法直接实现的， stl 的堆就是优先队列

堆
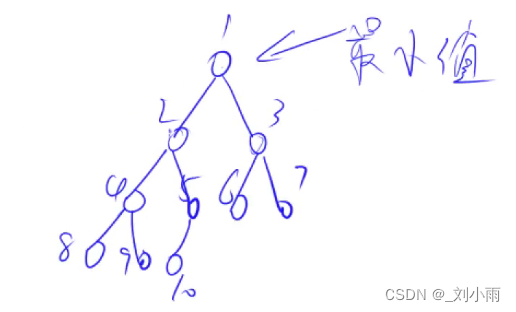
堆是一个完全二叉树（最后一层节点是左右依次排布的）

小根堆为例
每一个节点都小于等于父节点， 根节点就是最小值。

实现：

• 一维数组实现
  
  
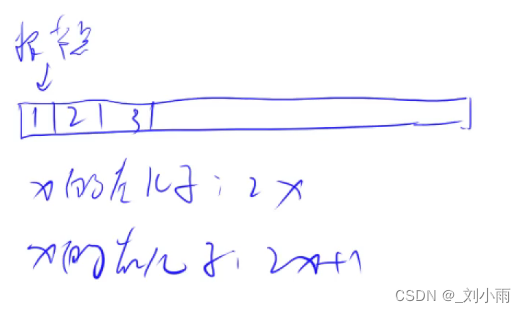
• 有两个操作 down(x) 、up(x)
  顾名思义： 把节点往上移或者往下移动

down(x) ： 如果把一个点的值变大了，就需要向下移动；跟叶子节点比较

up(x) ： 如果把一个点的值变小了，就需要向上移动；跟父节点比较

如何通过这两个操作实现前面的5个因素呢 heap 表示堆，size表示大小

1. heap[++size] = x; up(size);
2. heap[1]
3. heap[1] = heap[size]; size --; down(1); // 最小值不好直接删除，需要用最后一个值覆盖，然后调整堆
4. heap[k] = heap[size]; size --; down(k); up(k); // 只会执行1个操作
5. heap[k] = x; down(k), up(k);

题目

输入一个长度为 n 的整数数列，从小到大输出前 m 小的数。

输入格式
第一行包含整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

输出格式
共一行，包含 m 个整数，表示整数数列中前 m 小的数。

数据范围
1≤m≤n≤105，
1≤数列中元素≤109
输入样例：
5 3
4 5 1 3 2
输出样例：
1 2 3

思路：
只涉及排序，分析一下就用到了操作中的2、3 只涉及到down 操作

code:

#include <iostream>
using namespace std;

const int N =  100010;
int n,m;
int h[N], cnt;

void down(int u)
{
    // 核心操作就是看根节点、左儿子、右儿子，哪个是最小值
    int t = u;  // 用t保存 最小的数字
    if(u * 2 <= cnt && h[u * 2] < h[t])  t = u * 2;   // 保证左儿子存在， 并且左儿子小于父亲
    if(u *2 + 1<= cnt && h[u * 2 + 1] < h[t] ) t = u * 2 + 1; // 保证右儿子存在， 并且右儿子小于当前的小的点
    if(u != t)
    {
        swap(h[t], h[u]);  // 交换使得最小值在上面
        down(t);  // 递归处理
    }
}

void up(int u)
{
	while(u / 2 && h[u / 2] > h[u]) // 如果存在父节点且父节点大
	{
		swap(h[u / 2], h[u]);  // 交换
		u /= 2;     // 递归处理
	}
}

int main()
{
    cin >> n >> m;  
    for(int i = 1; i<=n; i++) cin >> h[i];
    cnt = n;
    
     // 初始化堆，从n / 2开始, 能使时间复杂度为O(n), 直接从n开始就会是O(logn)
    for(int i = n/2; i; i--) down(i);      
    
    while(m--)  // 取出前m个小的数字
    {
        cout << h[1] << ' ';   // 取出小根堆的最小数字
        h[1] = h[cnt];  // 将堆底元素（最后一个）放在第一位置
        cnt --;         // 总的个数 - 1
        down(1);        // 向下调整堆，维护使得最上面元素是最小的元素
    }
    return 0;
}