二叉树:
就是一棵树中每个结点最多只有两个结点,可以没有结点,也可以只有一个结点,也可以为空结点
下面说一下二叉树的常见形态:
????????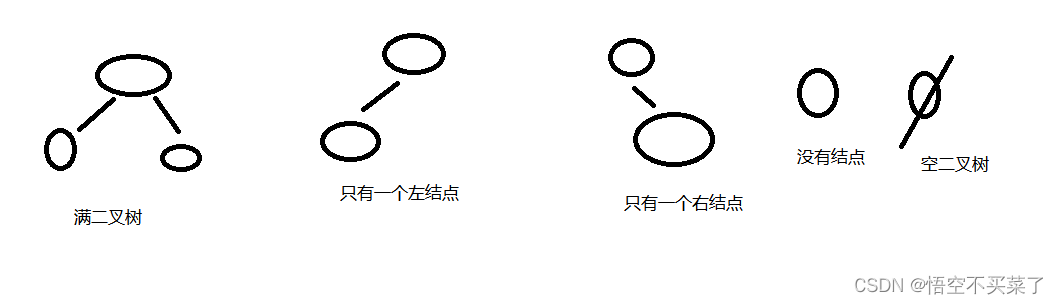
满二叉树与完全二叉树的区别:
? ? ? ? 满二叉树就是除了叶子结点之外,每一个结点都有两个孩子
? ? ? ? 完全二叉树就是每一个结点不一定有两个孩子,但是如果出现在同一层,完全二叉树结点的i位置与满二叉树结点的?i位置编号相同,就是完全二叉树。
? ? ? ? 所以,满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树
然后来说一下二叉树的性质:
????????1.在二叉树的i层最多有2^i-1个结点(i>0)
????????2.深度为k的二叉树最多有2^k - 1个结点(k>0)
????????3.对于任何一棵二叉树,若度为2的结点数有n2个,则叶子数n0必定为n2+1(n0=n2+1)
? ? ? ? 4.具有n个结点的完全二叉树深度必为
? ? ? ? ?5.对于完全二叉树,从上到下,从左到右,则编号为i的结点,其左孩子必为2i,右孩子编号为2*i + 1,其双亲的编号必为i/2(i=1时候为根)
二叉树的遍历:
? ? ? ? 大概会分为三种情况,这三种情况的讨论,就是根据到底是先遍历根,还是在中间遍历根,还是说在最后遍历根,也就分为了先序遍历(DLR),中序遍历(LDR),后序遍历(LRD)
? ? ? ? D:根 L: 左结点 R:右结点
? ? ? ? 先来看一个二叉树:
????????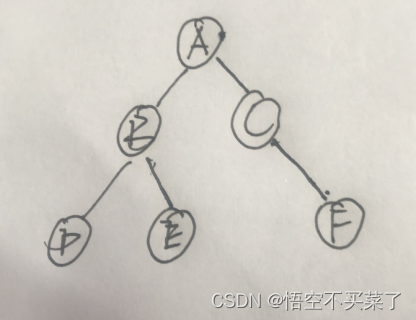
? ? ? ? 先来说一下先序遍历(DLR)
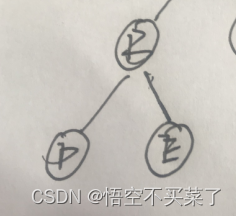
? ? ? ????????? 先根在左在右:比如一个函数r(从A传入结点),然后先把A打印,毕竟是先序嘛,然后去遍历左边,也就是走下面遍历
????????????????
? ? ? ? ? ? ? ? 这边函数栈就是
????????????????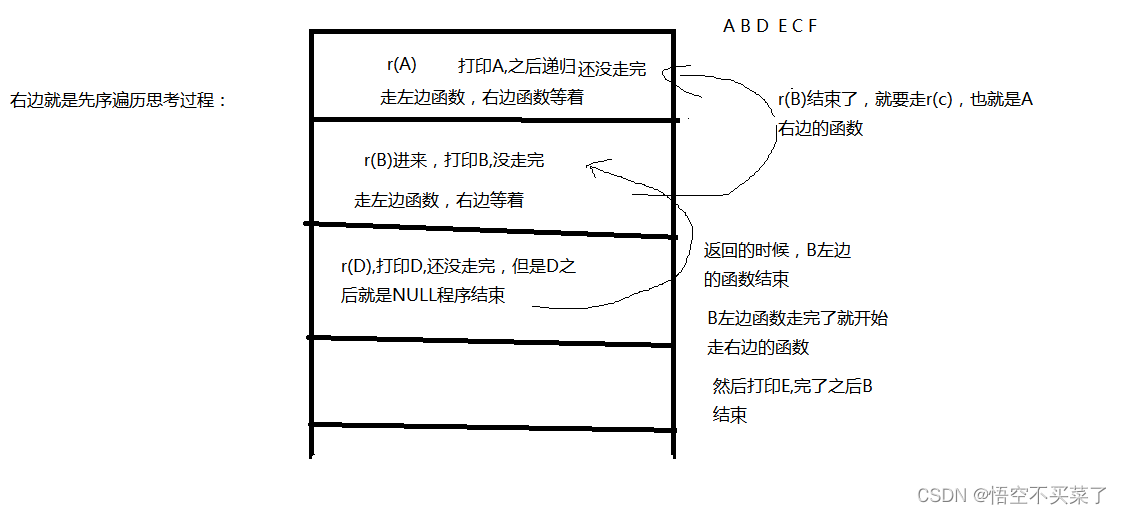 ?
?
?????????
话不多说,直接上代码:
????????
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
typedef struct _binary_node binary_node;
struct _binary_node
{
char ch;
binary_node *lchild;
binary_node *rchild;
};
void recursion_print(binary_node *node)
{
if (node == NULL) {
return;
}
printf("%c ", node->ch);
recursion_print(node->lchild);
recursion_print(node->rchild);
}
int main()
{
//靠靠靠靠靠靠靠
binary_node node_a = { 'A', NULL, NULL };
binary_node node_b = { 'B', NULL, NULL };
binary_node node_c = { 'C', NULL, NULL };
binary_node node_d = { 'D', NULL, NULL };
binary_node node_e = { 'E', NULL, NULL };
binary_node node_f = { 'F', NULL, NULL };
node_a.lchild = &node_b;
node_a.rchild = &node_c;
node_b.rchild = &node_e;
node_b.lchild = &node_d;
node_c.rchild = &node_f;
//靠靠
recursion_print(&node_a);
return 1;
}
?运行结果:
????????
? 当然了,二叉树肯定不至于递归,所以,比如计算二叉树叶子的数目,二叉树的高度,又比如拷贝一棵二叉树,下面上完整代码:
binary_tree.c
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
typedef struct _binary_node binary_node;
struct _binary_node
{
char ch;
binary_node *lchild;
binary_node *rchild;
};
void recursion_print(binary_node *node)
{
if (node == NULL) {
return;
}
printf("%c ", node->ch);
recursion_print(node->lchild);
recursion_print(node->rchild);
}
void calc_leaf_num(binary_node *node,int *p)
{
//程序的结束条件
if(node == NULL) {
return ;
}
//left and right is null
if(node->lchild == NULL && node->rchild == NULL) {
(*p)++;
}
calc_leaf_num(node->lchild,p);//传入计算数量变量的地址
calc_leaf_num(node->rchild,p);
}
//计算树高度
int get_tree_high(binary_node *node)
{
if(node == NULL) {
return 0;
}
//递归计算左右两边树的高度
int left_high = get_tree_high(node->lchild);
int right_high = get_tree_high(node->rchild);
return left_high > right_high ? left_high + 1 : right_high + 1;
}
//拷贝二叉树就是在堆上面开辟一个空间
//来存放二叉树的每一个结点
//最后返回头部结点
binary_node* copy_tree(binary_node *node)
{
if(node == NULL){
return NULL;
}
//还是要遍历左树,在遍历右树
binary_node* lnode = copy_tree(node->lchild);
binary_node* rnode = copy_tree(node->rchild);
//每一个结点都要干一件事儿
binary_node *new_node = (binary_node*)malloc(sizeof(binary_node));
if(new_node != NULL) {
new_node->ch = node->ch;
new_node->lchild = lnode;
new_node->rchild = rnode;
}
return new_node;
}
//释放拷贝的这棵树
void free_tree(binary_node *node)
{
if(node == NULL) {
return;
}
free_tree(node->lchild);
free_tree(node->rchild);
//在此之前看一下被释放的结点
printf("%c被释放了\n",node->ch);
free(node);//释放这个结点
}
int main()
{
binary_node node_a = { 'A', NULL, NULL };
binary_node node_b = { 'B', NULL, NULL };
binary_node node_c = { 'C', NULL, NULL };
binary_node node_d = { 'D', NULL, NULL };
binary_node node_e = { 'E', NULL, NULL };
binary_node node_f = { 'F', NULL, NULL };
node_a.lchild = &node_b;
node_a.rchild = &node_c;
node_b.rchild = &node_e;
node_b.lchild = &node_d;
node_c.rchild = &node_f;
recursion_print(&node_a);
int leaf_num = 0;
calc_leaf_num(&node_a,&leaf_num);
printf("叶子结点数目为:%d\n",leaf_num);
int tree_high = get_tree_high(&node_a);
printf("叶子数目为:%d\n",tree_high);
//拷贝二叉树
binary_node *node = copy_tree(&node_a);
//然后递归遍历一下这个二叉树
printf("\n-------------\n");
recursion_print(node);
printf("\n-----\n");
//释放拷贝的每一个结点
//二叉树非递归遍历
free_tree(node);
return 1;
}
????????
?????