[数据结构与算法]学习笔记-排序算法

参考博文：各种排序-从这篇文章中记录了学习笔记（搬运过来），掌握了原理，代码一定要结合图解手撸一遍。

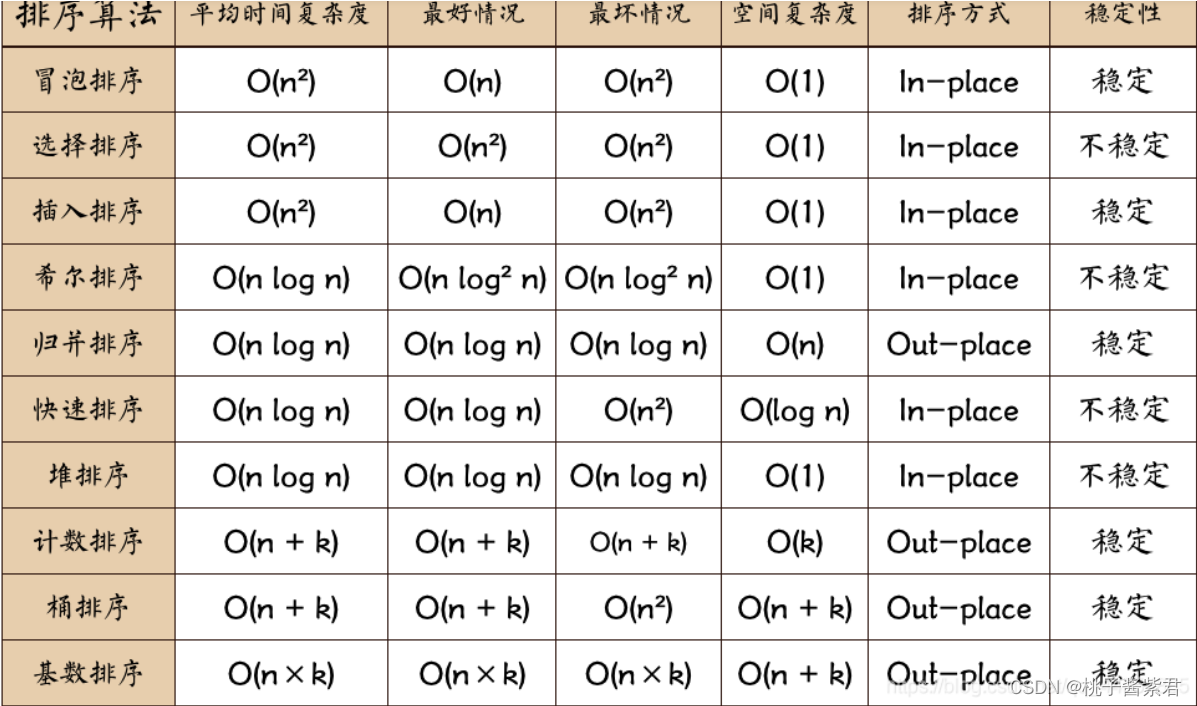
1、冒泡排序

。。。待写

2、选择排序

2.1 算法思想

• 在未排序的序列中找到最小（大）元素，存放到排序序列的起始位置。
• 从剩下未排序元素中继续寻找最小（大）元素，然后放到自己已排序的序列的末尾。
• 以此类推，直到所有元素排序完毕。

时间复杂度O(n^2)

2.2 图解

2.3 代码

//选择排序（升序）
void selectionSort(int* arr,int len)
{
	//从第一个位置找，共找len-1个最小数
	for (int i = 0; i < len - 1; i++)
	{
		int min = i;//min为最小值位置 初始认为i处是最小
		//接下来找到最小数放到第i个位置
		for (int j = i + 1; j < len; j++)
		{
			if (arr[j] < arr[min])
				min = j;			//如果找到更小的，就记录当前位置
		}
		swap(arr[i], arr[min]);		//最后将未排序中找到的最小值和第i个位置交换
	}
}

3、插入排序

3.1 算法思想
将无序元素插到有序元素中去

• 步骤1: 从第一个元素开始，该元素可以认为已经被排序；
• 步骤2: 取出下一个元素，在已经排序的元素序列中从后向前扫描；
• 步骤3: 如果该元素（已排序）大于新元素，将该元素移到下一位置（腾位置）；
• 步骤4: 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
• 步骤5: 将新元素插入到该位置后；
• 步骤6: 重复步骤2~5。

时间复杂度O(n^2),不稳定,

3.2 图解

3.3 代码

//插入排序（升序）
void insertSort(int* arr,int len)
{
	//第1个位置已叫排序，从第2个位置到最后一个位置插入len-1次
	for (int i = 1; i < len; i++)
	{
		//第i个位置装配，开始找插入位置
		int temp = arr[i];
		int j = i - 1;
		while (j >= 0 && temp < arr[j])//条件分两种情况：1、插入中间 2、插入头部
		{
			arr[j + 1] = arr[j];
			j--;
		}
		//j位置的值比temp小，就插入j+1位置
		arr[j + 1] = temp;
	}
}

4、快速排序

4.1 算法思想

• 选第一个数为标准。
• 将比基准小的数据交换到前面，比基准大的交换到后面
• 对左边的空间和右边的空间重复，直到各区间只有一个数字

4.2 图解

4.3 代码

//快速排序（升序） 使用了迭代方法，迭代函数详细描述一层运算
void quickSort(int* arr,int left,int right)
{
	//设置迭代截至条件
	if (left >= right)	return;
	//两个标志承接左右下标 设置初始基准值
	int begin = left;
	int end = right;
	int key = arr[end];
	//开始当前一层的运算
	while (begin < end)
	{
		//基准左边一般为小 找大
		while (begin < end && arr[begin] <= key)	begin++;
		arr[end] = arr[begin];//如果找到大的，将其提取到右边end处
		//基准右边一般为大 找小
		while (begin < end && arr[end] >= key)	end--;
		arr[begin] = arr[end];//如果找到小的，将其提取到左边begin处
	}
	arr[end] = key;//最后将基准放在begin和end交界处
	//开启下一层运算
	quickSort(arr, left, end - 1);//基准左边排序交给迭代函数
	quickSort(arr, end + 1, right);//基准右边排序交给迭代函数
}

5、堆排序

5.1 算法思想

• 如果要从小到大排序，建立大堆，根节点大于左右子树。
• 将根结和最后一个元素交换，并且树的元素个数减1。
• 重复1~2，直到只剩一个元素。

参考博文：堆排序(C语言)

定义了以下几种操作：
（1）最大堆调整（Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
（2）创建最大堆（CreateHeap）：将堆中的所有数据重新排序
（3）堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

堆是一个近似完全二叉树的结构
数组a[k]与二叉树的性质：
父节点：(k-1)/2
左子节点：2k+1
右子节点：2k+2

5.2 图解

5.3 代码

//堆排序
//子函数：最大对调整 迭代 （前提是其子节点已经成为最大堆，检验这个父节点有没有实力，没有则为其安排在适合的位置，谁有能力谁上）
void heapify(int* arr,int len,int k)
{
	//迭代继续条件 检验父节点
	if (k < len)
	{
		int max = k;			//假设父节点最大
		int s1 = 2 * k + 1;		//子节点索引
		int s2 = 2 * k + 2;		//子节点索引
		//看看子节点有没有更强的
		if (s1<len && arr[s1]>arr[max])	max = s1;
		if (s2<len && arr[s2]>arr[max])	max = s2;
		//如果有强的，子节点上，父节点继续和下边儿比较
		if (max != k)
		{
			swap(arr[max], arr[k]);
			heapify(arr, len, max);//退下来的父节点继续看看这个位置他能把握住吗
		}
	}
}
//堆排序函数
void heapSort(int* arr, int len)
{
	//1、创建最大堆 根节点为最大数
	int last_node = len - 1;
	int last_parent = (last_node - 1) / 2;//最后一个父节点
	//从低向上 创建最大堆 每一小步都是用最大堆调整
	for (int i = last_parent; i >= 0; i--)
		heapify(arr, len, i);
	//2、每次根节点为最大数 放后边儿 升序排序
	for (int i = len - 1; i >= 0; i--)
	{
		swap(arr[0], arr[i]);
		heapify(arr, i, 0);//这里剩余数量正好是i 对新的根节点重新调整审视（因为已经创建后的最大堆，除了根节点，其他都符合最大堆性质）
	}
}

6、希尔排序

6.1 算法思想
将数组元素分成若干组，每组分别进行插入排序，使整个数组逐渐变成部分有序数组，再慢慢减少所分的组数，最终合并成一个组 。

将数组多次分组，分别进行插入排序—改进的插入排序。

参考博文：排序算法之希尔排序、希尔排序C++实现

6.2 图解

6.3 代码

//希尔排序
void shellSort(int* arr,int len)
{
	int group = len / 2;//分组数
	//不同组数下，对每组插入排序
	while (group >= 1)
	{
		//希尔排序下的插入排序
		//外层循环 确定要选哪些点插入
		for (int i = group; i < len; i++)
		{
			int temp = arr[i];//要插入的值存入临时变量
			int j = i - group;//插入已排好序的数组用到的指针
			//内层循环 插入
			while (j>=0&&temp<=arr[j])
			{
				arr[j + group] = arr[j];//正常都是慢慢排查
				j = j - group;
			}
			arr[j + group] = temp;//找到位置了 插入
		}
		group /= 2;//该换小点儿的分组了
	}
}

7、计数排序

7.1 算法思想

• 1、找出待排序的数组最大和最小的元素
• 2、统计数组中每个值为i∈[min:1:max]的元素出现的个数，存入数组c的第i-min项
• 将下标+min的值根据在数组c中的个数存到原数组中。

本算法图解更容易理解

7.2 图解

7.3 代码
时间复杂度：O(n+k)，n容量的原数组，k容量的计数数组，实际分别遍历了两个数组，所有好坏情况都是O(n+k)。
空间复杂度：O(k)，新建了k容量的计数数组。

//计数排序
void countSort(int* arr, int len)
{
	//1、找最大最小值
	int min = arr[0];
	int max = arr[0];
	for (int i = 0; i < len; i++)
	{
		if (arr[i] < min)	min = arr[i];
		if (arr[i] > max)	max = arr[i];
	}
	//2、创建计数数组
	int len_count = max - min + 1;//计数数组长度
	int* arr_count = new int[len_count];
	for (int i_count = 0; i_count < len_count; i_count++)
		arr_count[i_count] = 0;
	for (int i = 0; i < len; i++)//核心，为每个数计数
	{
		arr_count[arr[i] - min] += 1;
	}
	//3、计数数组-按顺序放回->原数组
	int i_total = 0;
	for (int i_count = 0; i_count < len_count; i_count++)
	{
		for (int i_temp = 0; i_temp < arr_count[i_count]; i_temp++)
		{
			arr[i_total++] = min + i_count;//装入真实的数
		}
	}
}

8、基数排序

8.1 算法思想

• 取得数组中的最大数，并取得位数。
• 根据个位数值大小，对数组进行排序（实际放0~9的桶里进行计数排序）；
• 重复上一步骤，依次根据更高位数值进行排序，直至到达最高位；

参考博文：C++排序算法之基数排序

8.2 图解

8.3 代码

//基数排序
//获得数组中最大数的位数
int maxBit(int* arr, int len)
{
	int bit_num = 0;
	for (int i = 0; i < arr[i]; i++)//遍历数组
	{
		//获取当前数的位数
		int temp = arr[i];
		int bit_temp = 0;
		while (temp > 0)
		{
			temp /= 10;
			bit_temp++;
		}
		//比较是否是最大位数
		if (bit_temp > bit_num)
			bit_num = bit_temp;
	}
	return bit_num;
}
//基数排序的简单实现
void radixSort(int* arr, int len)
{
	int bit_max = maxBit(arr, len);		//获得数组中最大数的位数
	vector<vector<int>> buckets(10);	//新建10个桶
	int r = 1;							//作为除数
	for (int i_bit = 0; i_bit < bit_max; i_bit++)//从低位向高位遍历
	{
		//1、遍历数组，将数放桶里
		for (int i = 0; i < len; i++)
		{
			int num_temp = (arr[i] / r) % 10;//取特定的那一位
			buckets[num_temp].push_back(arr[i]);
		}
		//2、遍历桶，按桶的顺序放回数组
		int i_origin = 0;
		for (int i_bucket = 0; i_bucket < 10; i_bucket++)
		{
			if (!buckets[i_bucket].size()) continue;
			for (vector<int>::iterator itr_num = buckets[i_bucket].begin(); itr_num != buckets[i_bucket].end(); itr_num++)
			{
				arr[i_origin++] = *itr_num;
			}
			buckets[i_bucket].clear();//用完顺便清空，以便下次再用。
		}
		r *= 10;
	}
}

9、桶排序

9.1 算法思想

是计数排序的进化版

• 设置一个定量的数组当作空桶子。
• 寻访序列，并且把项目一个一个放到对应的桶子去（将数组分段划分、按位数划分等）。
• 对每个非空的桶子进行排序（其他适合小范围的排序，如插入排序）。
• 从不是空的桶子里把项目再放回原来的序列中。

参考博文：C/C++桶排序

9.2 图解

9.3 代码

//桶排序
void bucketSort(int* arr, int len)
{
	//寻找最大最小值
	int min_value = arr[0];
	int max_value = arr[0];
	for (int i = 1; i < len; i++)
	{
		if (arr[i] < min_value)	min_value = arr[i];
		if (arr[i] > max_value) max_value = arr[i];
	}
	//初始化桶，将数组的数据按某一分组装入桶中
	int bucketsize = 5;											//桶大小
	int buckets_num = (max_value - min_value) / bucketsize + 1;	//桶数量
	vector<vector<int>> buckets(buckets_num);
	for (int i = 0; i < len; i++)
	{
		int index = (arr[i] - min_value) / bucketsize;
		buckets[index].push_back(arr[i]);
	}
	//对每个桶排序，装回原数组
	int i_origin = 0;		//全程记录原数组索引
	for (int i_bucket = 0; i_bucket < buckets_num; i_bucket++)
	{
		if (!buckets[i_bucket].size()) continue;//排除空桶
		//给当前桶排序（插入排序）
		for (int i_sort = 1; i_sort < buckets[i_bucket].size(); i_sort++)
		{
			int temp_sort = buckets[i_bucket][i_sort];
			int j_sort = i_sort - 1;//关键索引
			while (j_sort >= 0 && temp_sort < buckets[i_bucket][j_sort])
			{
				buckets[i_bucket][j_sort + 1] = buckets[i_bucket][j_sort];
				j_sort--;
			}
			buckets[i_bucket][j_sort + 1] = temp_sort;
		}
		//将排好序的桶数据放回原数组
		for (int i_sort = 0; i_sort < buckets[i_bucket].size(); i_sort++)
		{
			arr[i_origin++] = buckets[i_bucket][i_sort];
		}
	}
}

/--------------------------------------------------------------------------------------------------------------------------------/

x、排序

x.1 算法思想

x.2 图解

x.3 代码