题目列表
1.判断矩阵是否是一个 X 矩阵
题目描述
如果一个正方形矩阵满足下述 全部 条件,则称之为一个 X 矩阵 :
矩阵对角线上的所有元素都 不是 0
矩阵中所有其他元素都是 0
给你一个大小为 n x n 的二维整数数组 grid ,表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ,返回 true ;否则,返回 false 。
示例 1:

输入:grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出:true
解释:矩阵如上图所示。
X 矩阵应该满足:绿色元素(对角线上)都不是 0 ,红色元素都是 0 。
因此,grid 是一个 X 矩阵。
示例 2:
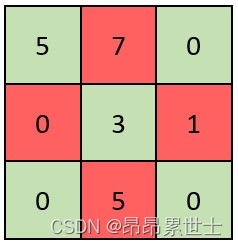
输入:grid = [[5,7,0],[0,3,1],[0,5,0]]
输出:false
解释:矩阵如上图所示。
X 矩阵应该满足:绿色元素(对角线上)都不是 0 ,红色元素都是 0 。
因此,grid 不是一个 X 矩阵。
提示:
n == grid.length == grid[i].length
3 <= n <= 100
0 <= grid[i][j] <= 105
分析
考察矩阵主副对角线的性质,主对角线i == j,副对角线i + j == n - 1。
代码
class Solution {
public:
bool checkXMatrix(vector<vector<int>>& grid) {
int n = grid.size();
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
if(i == j || i + j == n - 1){
if(!grid[i][j]) return false;
}
else if(grid[i][j]) return false;
}
}
return true;
}
};
2.统计放置房子的方式数
题目描述
一条街道上共有 n * 2 个 地块 ,街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。
现要求街道同一侧不能存在两所房子相邻的情况,请你计算并返回放置房屋的方式数目。由于答案可能很大,需要对 109 + 7 取余后再返回。
注意,如果一所房子放置在这条街某一侧上的第 i 个地块,不影响在另一侧的第 i 个地块放置房子。
示例 1:
输入:n = 1
输出:4
解释:
可能的放置方式:
- 所有地块都不放置房子。
- 一所房子放在街道的某一侧。
- 一所房子放在街道的另一侧。
- 放置两所房子,街道两侧各放置一所。
示例 2:
输入:n = 2
输出:9
解释:如上图所示,共有 9 种可能的放置方式。
提示:
1 <= n <= 104
分析
由于两边街道完全一样,而且放置互不干扰,所以如果一边街道的放置方案数是x,那么根据乘法原理,两边街道的放置方案数就是x2。
现在我们要求的就是一边街道的放置方式,我看这题的数据范围是1w,周赛时写了个平方级别的DP,提交一直TLE,手动执行显示几百毫秒,可见存在线性的解法这题就卡了时间。DP的状态表示很重要,状态表示决定了后面算法的复杂度以及复杂程度。
本题第i个地块可以选择放与不放,符合状态机模型,可以用f[i][1]表示前i个地块中放置方式中第i个地块放置了房子的方案数,f[i][0]表示前i个地块中放置方式中第i个地块不放置了房子的方案数,第i个地块只能放或者不放,这样划分不重不漏。下面考虑状态转移,如果第i个地块选择放置,那么前一个地块必然不能放置放置,所以f[i][1] = f[i-1][0],这里在第i个地块放置房子是不允许前i - 2个地块的放置方式的,所以可以直接继承第i - 1个地方不放置房子的方案数即可。如果第i个地块不放置房子,那么前一个地块可放可不放,f[i][0] = f[i-1][0] + f[i-1][1]。
如果不想使用DP求解,也可以找规律,一边街道的放置方式随着n的递增方案数依次是2 3 5 8 13 21…,可以发现就是斐波那契数列,求出斐波那契数列,加下偏置值就是答案了。
代码
class Solution {
public:
int countHousePlacements(int n) {
const int MOD = 1000000007;
vector<vector<int> > f(n + 1,vector<int>(2,0));
f[1][0] = f[1][1] = 1;
for(int i = 2;i <= n;i++){
f[i][0] = (f[i-1][0] + f[i-1][1]) % MOD;
f[i][1] = f[i-1][0];
}
int res = (f[n][0] + f[n][1]) % MOD;
res = (long long)res * res % MOD;
return res;
}
};
3.拼接数组的最大分数
题目描述
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,长度都是 n 。
你可以选择两个整数 left 和 right ,其中 0 <= left <= right < n ,接着 交换 两个子数组 nums1[left…right] 和 nums2[left…right] 。
例如,设 nums1 = [1,2,3,4,5] 和 nums2 = [11,12,13,14,15] ,整数选择 left = 1 和 right = 2,那么 nums1 会变为 [1,12,13,4,5] 而 nums2 会变为 [11,2,3,14,15] 。
你可以选择执行上述操作 一次 或不执行任何操作。
数组的 分数 取 sum(nums1) 和 sum(nums2) 中的最大值,其中 sum(arr) 是数组 arr 中所有元素之和。
返回 可能的最大分数 。
子数组 是数组中连续的一个元素序列。arr[left…right] 表示子数组包含 nums 中下标 left 和 right 之间的元素(含 下标 left 和 right 对应元素)。
示例 1:
输入:nums1 = [60,60,60], nums2 = [10,90,10]
输出:210
解释:选择 left = 1 和 right = 1 ,得到 nums1 = [60,90,60] 和 nums2 = [10,60,10] 。
分数为 max(sum(nums1), sum(nums2)) = max(210, 80) = 210 。
示例 2:
输入:nums1 = [20,40,20,70,30], nums2 = [50,20,50,40,20]
输出:220
解释:选择 left = 3 和 right = 4 ,得到 nums1 = [20,40,20,40,20] 和 nums2 = [50,20,50,70,30] 。
分数为 max(sum(nums1), sum(nums2)) = max(140, 220) = 220 。
示例 3:
输入:nums1 = [7,11,13], nums2 = [1,1,1]
输出:31
解释:选择不交换任何子数组。
分数为 max(sum(nums1), sum(nums2)) = max(31, 3) = 31 。
提示:
n == nums1.length == nums2.length
1 <= n <= 105
1 <= nums1[i], nums2[i] <= 104
分析
首先看下交换num1和nums2两个数组[l,r]区间的结果是啥,交换部分的和分别是nums1[l] +…+ nums1[r]和nums2[l] +…+ nums2[r],对于num1而言,交换操作使得它的和增加了(nums2[l] - nums1[l]) +…+ (nums2[r] - nums1[r]),令nums3[i] = nums2[i] - nums1[i],原式就转化为了nums3[l] +…+ nums3[r],如果想要交换后nums1的和增加最多,只需要nums3数组的部分和最大。这样一来,原问题就转化为了求nums3数组的最大连续子序列和了。
准确说还需要求下nums3数组的最小连续子序列和,只要部分和最小,交换后nums2数组的和才是最大的。
代码
class Solution {
public:
int s[100005] = {0};
int f1[100005] = {0};
int f2[100005] = {0};
int maximumsSplicedArray(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size(),s1 = 0,s2 = 0;
for(int i = 0;i < n;i++){
s1 += nums1[i];
s2 += nums2[i];
s[i] = nums1[i] - nums2[i];
}
f1[0] = f2[0] = s[0];
int p = 0,q = 0;
for(int i = 1;i < n;i++){
f1[i] = f2[i] = s[i];
if(f1[i-1] > 0) f1[i] += f1[i-1];
if(f2[i-1] < 0) f2[i] += f2[i-1];
p = max(p,f1[i]);
q = min(q,f2[i]);
}
int res = max(s1 - q,s2 + p);
return res;
}
};
4.从树中删除边的最小分数
题目描述
存在一棵无向连通树,树中有编号从 0 到 n - 1 的 n 个节点, 以及 n - 1 条边。
给你一个下标从 0 开始的整数数组 nums ,长度为 n ,其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ,长度为 n - 1 ,其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。
删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案,定义如下步骤以计算其分数:
分别获取三个组件 每个 组件中所有节点值的异或值。
最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。
例如,三个组件的节点值分别是:[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ,最小异或值是 3 ,分数是 8 - 3 = 5 。
返回在给定树上执行任意删除边方案可能的 最小 分数。
示例 1:
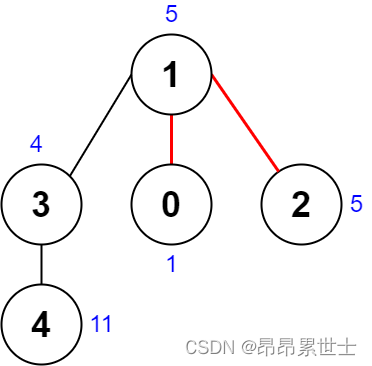
输入:nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出:9
解释:上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ,值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ,值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ,值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值,10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。
示例 2:
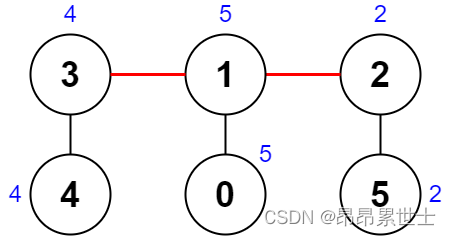
输入:nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出:0
解释:上图展示了一种删除边方案。 - 第 1 个组件的节点是 [3,4] ,值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ,值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ,值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值,0 - 0 = 0 。
无法获得比 0 更小的分数 0 。
提示:
n == nums.length
3 <= n <= 1000
1 <= nums[i] <= 108
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵有效的树
分析
周赛时T2状态表示没有选取好,导致浪费了挺多时间,T4周赛结束后几分钟才a掉,提交下发现还是个双百的算法。
如果本题只要求删掉一条边,那么很简单,遍历的时候尝试删掉每棵子树就可以求出来。我们可以将删两条边的问题转化为删一条边的问题,也就是遍历下n - 1条边,每次选择删掉一条边都重新建图,少连一条边,就相当于删掉了一条边,这样原本连通的树在删掉a到b的这条边后就变成了两个以a和b为根的树,第二条要删除的边可以分别遍历a和b求出来。
也就是说,删掉a到b的连边,需要先求出以a为根的子树的异或和x1,以b为根的子树的异或和x2,遍历以a为根的子树时,如果想要删掉u连向某个孩子节点v的边,那么可以求出以v为根的子树的异或和y,这样一来a树中剩下部分的异或和就是x1 ^ y,将y、x1^y以及x2这三部分的异或和中最大值和最小值求出来相减就可以更新解了;同理还需要遍历以b为根的子树,枚举下第二条要删除的边在b树上的情形。
我周赛时采取的办法是只去建立一遍图,然后使用比较巧妙的办法删去边。由于一共有n个节点n条边,所以肯定存在连接着两个节点的节点,也就是度为2的节点,我们将其中一个度为2的节点设置为树的根节点,为什么要这样做,后面会解释的。首先对原树做下dfs,求出以每个节点为根的子树的异或和并保存到s1数组里。然后我们尝试删掉一条边,其实在遍历时就相当于删掉一个点,也就是遍历到这个点时就当做没看见。

如上图所示,我们第一个要删掉的边删掉后,就相当于从原树中摘下一棵以t为根的子树,并不需要真的斩断这条边,而是在遍历是t的父节点遍历到t这个分支时选择无视即可,这样可以求出删掉一条边后的异或和,可以提前预处理下整棵树的异或和total,然后第一条删掉的边去掉的子树的异或和就是s1[t],s1里存储着我们对原树遍历得到的异或和。我们遍历删掉一条边的树时,比如在上图中砍断第二条边,可以求出摘掉的子树的异或和x,这样一来树中两部分的异或和求出来了,剩下部分的异或和就是total ^ x ^ s1[t],按照前面一样的方法更新解即可。
这种方法的巧妙之处在于将删掉一条边转化为删掉一个以t为根的子树,然后在剩下的子树里删第二条边,删边不方便,但是删掉一个顶点简单的遍历就行了。为什么要选择有多个孩子的节点作为根节点呢?因为一旦根节点只有一个孩子,那么枚举时删掉了它唯一的孩子节点,就没法在剩下的一个节点里再去删边了。另一个方便的地方在于删掉一条边后我们不用在剩下的两部分中都去尝试删掉一条边,因为删掉树中的任一个节点,就相当于枚举了所有删掉第一条边的情形,剩下的部分足够我们删第二条边了。
当然本题还有其他解法,比如使用括号引理初始化节点的生命周期后,二重循环直接枚举要删掉的两条边,代码更简洁但是需要分类讨论。
代码
class Solution {
public:
vector<int> e[1005];
int ans = 1e9,total = 0;
int s1[1005],s2[1005];
int dfs(int u,int fa,vector<int>& nums){
int s = nums[u];
for(auto x : e[u]){
if(x != fa) s ^= dfs(x,u,nums);
}
s1[u] = s;
return s;
}
int reduce(int u,int fa,int t,vector<int>& nums){
int s = nums[u];
for(auto x : e[u]){
if(x != fa && x != t) s ^= reduce(x,u,t,nums);
}
for(auto x : e[u]){
if(x != fa && x != t){
int r = total ^ s1[t] ^ s2[x];
int t1 = max(s1[t],max(r,s2[x]));
int t2 = min(s1[t],min(r,s2[x]));
ans = min(t1 - t2,ans);
}
}
s2[u] = s;
return s;
}
int minimumScore(vector<int>& nums, vector<vector<int>>& edges) {
int n = nums.size();
for(auto x : nums) total ^= x;
for(auto x : edges){
int a = x[0],b = x[1];
e[a].push_back(b);
e[b].push_back(a);
}
int root = -1;
for(int i = 0;i < n;i++){
if(e[i].size() > 1) {
root = i;
break;
}
}
dfs(root,-1,nums);
for(int i = 0;i < n;i++){
if(i != root) reduce(root,-1,i,nums);
}
return ans;
}
};