基于上次分享没有处理结束的内容,但也有没用听过同学,所以在讲这个的时候会从头开始
外部排序
外部排序主要是处理在数据相对较大,直接无法排序或者很难保证安全性的情况下排序的一种排序,在处理外部排序的时候需要使用到辅助空间一般
举个例子
给你一个包含20亿个int类型整数的文件,计算机的内存只有2GB,怎么给它们排序?一个int数占4个字节,20个亿需要80亿字节,大概占用8GB的内存,而计算机只有2GB的内存,数据都装不下!那么这个时候我们需要对这个文件排序的话,最好的方法就是使用外部排序
处理外部排序需要提前了解其他相关的知识主要有归并排序和胜者树/败者树
归并排序
归并排序是一种内部排序,内部排序相对而言是更简单的一种排序,在处理的时候很容易得到其相关的信息,比如说空间复杂度还有时间复杂度等等
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:相对稳定
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有 序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤
?
正如上次我画的那张图一样将一个数字段进行分割。
2,14,6,4,3,9,1,23
这样的一个数列进行分割,得到了一个一个的数字,在这些数字当中两个两个的排序可以得到这样的数段
2? 14? ? 4? 6? ?3? 9? ? 1? 23
然后再将这四段归并成为两段
得到
2? 4? 6? 14? ? 1? 3? 9? 23
这个样子的数段。然后再对这样子的数段进行排序
得到:
1? 2? 3? 4? 6? 9? 14? 23
即排好序的情况。?
这里重要的是拆解和合并。在我演示的这个例子里面,进行的是两两拆分然后进行排序,这是最简单的排序方式
相关代码如下
using namespace std;
void Swap(int arr[], int a, int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
void combindArray(int array[], int left, int right, int mid){
//将[left,mid) 和数组[mid,right)进行合并
int* p = new int[right - left];
int i = 0;
int start = left;
int end = right;
int port = mid;
while (left < mid&&port < right){
if (array[left] < array[port]){
p[i++] = array[left++];
}
else{
p[i++] = array[port++];
}
}
while (left < mid){
p[i++] = array[left++];
}
while (port < right){
p[i++] = array[port++];
}
i = 0;
while (start < end){
array[start++] = p[i++];
}
delete[]p;
}
//1.平均切割区间
//2.分治处理左右两个小区间,直到size ==0 或者size ==1
//3.合并左右两个有序数组
void MergeSortInner(int array[], int left, int right){//此时我们的区间是[left,right)
if (left == right){
return;//size=0;
}
if (left + 1 == right){
return;
}
int mid = (left + right) / 2;
MergeSortInner(array, left, mid);
MergeSortInner(array, mid, right);
//合并两个区间的元素
combindArray(array, left, right, mid);
}
//归并排序就是将两个有序的区间进行合并,采用分治算法
void MergeSort(int array[], int size){
MergeSortInner(array, 0, size);
}
void printSort(int array[], int size){
for (int i = 0; i < size; i++){
cout << array[i] << " ";
}
cout << endl;
}
int main(){
int arr[] = { 5, 6, 8, 9, 5, 4, 2, 3, 1, 6 };
int size = sizeof(arr) / sizeof(arr[0]);
MergeSort(arr, size);
printSort(arr, size);
system("pause");
return EXIT_SUCCESS;
}
那么接下来重要的是处理外部排序的东西了,在这之前先学习一下胜者树和败者树?
胜者树和败者树是同属于多路平衡归并排序的一种处理,要知道外部排序主要做的处理是文件中的数据大小的排序,那么举一个例子:对于 10 个临时文件,当采用 2-路平衡归并时,若每次从 2 个文件中想得到一个最小值时只需比较 1 次;而采用 5-路平衡归并时,若每次从 5 个文件中想得到一个最小值就需要比较 4 次。以上仅仅是得到一个最小值记录,如要得到整个临时文件,其耗费的时间就会相差很大。
为了避免在增加 k 值的过程中影响内部归并的效率,在进行 k-路归并时可以使用“败者树”来实现,该方法在增加 k 值时不会影响其内部归并的效率。
败者树
败者树是一种树形选择结构,其本身就是一颗完全二叉树
举一个例子,我在处理一个数列{23,14,2,21,12,6}的时候,可以根据这个来创建完全二叉树,构建这个树的主要原因是为了筛选出来当前这个数列中存在的最小值。败者树在处理节点的时候使用的是对左右孩子进行比较,得到其中的失败者存入节点然后胜利者继续向上和其他胜利者比较当然也存在对一个一个的数组进行比较,那么首先需要对数组进行排序,将这个数组排序得到一个从小到大的数组,对其编号之后最对其进行对比。最后输入到节点的应该是这个的编号而不是这整个数组。
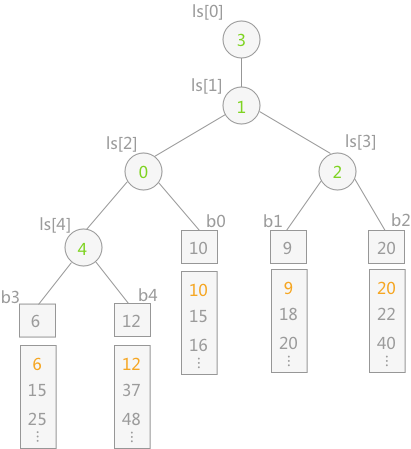
?
在这个使用的起码是三路以上的排序,那么很简单理解b3和b4在最小的进行对比之后保留输掉的最小的的在ls[4]这个节点中所以是4。接下来是6和10之间的对比,10作为败者被留到节点当中然后在6和9之间的比较,在其上存为ls[1],最后便在最上面存最后的胜者
#include <stdio.h>
#define k 5
#define MAXKEY 10000
#define MINKEY -1
typedef int LoserTree[k];//表示非终端结点,由于是完全二叉树,所以可以使用一维数组来表示
typedef struct {
int key;
}ExNode,External[k+1];
External b;//表示败者树的叶子结点
//a0-a4为5个初始归并段
int a0[]={10,15,16};
int a1[]={9,18,20};
int a2[]={20,22,40};
int a3[]={6,15,25};
int a4[]={12,37,48};
//t0-t4用于模拟从初始归并段中读入记录时使用
int t0=0,t1=0,t2=0,t3=0,t4=0;
//沿从叶子结点b[s]到根结点ls[0]的路径调整败者树
void Adjust(LoserTree ls,int s){
int t=(s+k)/2;
while (t>0) {
//判断每一个叶子结点同其双亲结点中记录的败者的值相比较,调整败者的值,其中 s 一直表示的都是胜者
if (b[s].key>b[ls[t]].key) {
int swap=s;
s=ls[t];
ls[t]=swap;
}
t=t/2;
}
//最终将胜者的值赋给 ls[0]
ls[0]=s;
}
//创建败者树
void CreateLoserTree(LoserTree ls){
b[k].key=MINKEY;
//设置ls数组中败者的初始值
for (int i=0; i<k; i++) {
ls[i]=k;
}
//对于每一个叶子结点,调整败者树中非终端结点中记录败者的值
for (int i=k-1; i>=0; i--) {
Adjust(ls, i);
}
}
//模拟从外存向内存读入初始归并段中的每一小部分
void input(int i){
switch (i) {
case 0:
if (t0<3) {
b[i].key=a0[t0];
t0++;
}else{
b[i].key=MAXKEY;
}
break;
case 1:
if (t1<3) {
b[i].key=a1[t1];
t1++;
}else{
b[i].key=MAXKEY;
}
break;
case 2:
if (t2<3) {
b[i].key=a2[t2];
t2++;
}else{
b[i].key=MAXKEY;
}
break;
case 3:
if (t3<3) {
b[i].key=a3[t3];
t3++;
}else{
b[i].key=MAXKEY;
}
break;
case 4:
if (t4<3) {
b[i].key=a4[t4];
t4++;
}else{
b[i].key=MAXKEY;
}
break;
default:
break;
}
}
//败者树的建立及内部归并
void K_Merge(LoserTree ls){
//模拟从外存中的5个初始归并段中向内存调取数据
for (int i=0; i<=k; i++) {
input(i);
}
//创建败者树
CreateLoserTree(ls);
//最终的胜者存储在 is[0]中,当其值为 MAXKEY时,证明5个临时文件归并结束
while (b[ls[0]].key!=MAXKEY) {
//输出过程模拟向外存写的操作
printf("%d ",b[ls[0]].key);
//继续读入后续的记录
input(ls[0]);
//根据新读入的记录的关键字的值,重新调整败者树,找出最终的胜者
Adjust(ls,ls[0]);
}
}
int main(int argc, const char * argv[]) {
LoserTree ls;
K_Merge(ls);
return 0;
}胜者树是和其相似的
最小堆和败者树
先介绍一下最小堆
最小堆有以下特点:
1、最小堆是一颗完全二叉树
2、每个父节点的值总是小于等于左右孩子节点的值
3、每个节点的子树都是一个堆树
堆常用一维数组结构存储,增删改查的时间复杂度都是 log(n)。操作流程举例:
1、插入操作
(1)将插入元素放到数组末尾
(2)从新插入元素位置开始,将数组头方向开始调整,或者树结构上说,就是向上调整
2、查询操作
(1)取出堆顶元素,并将数组最后一个元素赋值到堆顶
(2)树结构上,向下调整
那么为什么在使用外部排序的时候经常使用的是败者树而不是胜者树或者最小堆
它的插入和查询复杂度都是 log(n),可以说比较高效。不过,堆调整时,每个节点都需要和左右孩子进行比较,即需要两次比较,在外部排序中,也就是需要读取两次外存,那能不能再优化下呢?
于是,研究出了胜者树。胜者树只需要和兄弟节点进行比较,减少了一般的比较量。但是,胜者树还需要从父节点取一次值,并且,因为新插入的值取代了原先的最优胜者,这个新值向上调整的过程中,必定需要修改父节点的值,即必须要更新胜者。那能不能再优化呢?
既然有胜者树,那自然也有败者树。败者树解决了胜者树存在的弊端,只需要和父节点比较一次,并且新插入的值向上调整过程中,不一定要更新。
所以在使用外部排序的时候更好的是使用败者树进行排序