先说结果,可以走三步,但没必要,反而会影响效率。
下面是推导过程,摘自stackflow。
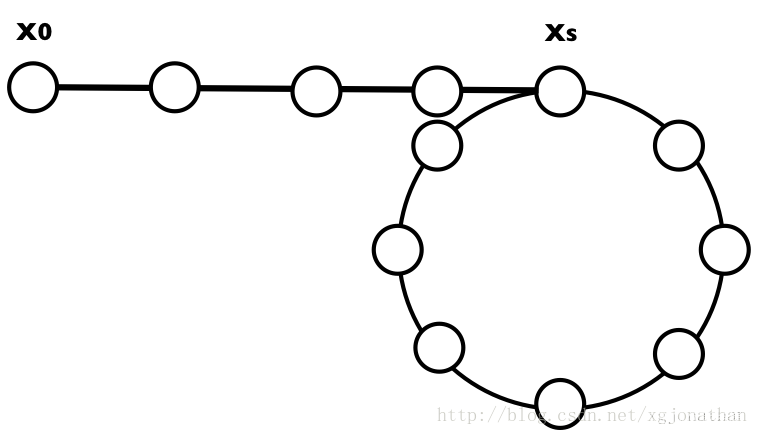
设非环的部分s步,环t步,快指针速度是慢指针的k倍,快慢指针在距离环开头的 j 步处相遇。
那么,相遇时,慢指针走了s+j,快指针走了s + j + m * t,(m是快指针在环中的圈数)
此时,快指针走的距离时慢指针的k倍,则有等式:
k * (s + j) = s + j + m * t
变换一下:
s + j = (m / k-1)t
根据上面的公式可知,等式左边是慢指针走的步数,是等式右边环长度的倍数,慢指针步数s + j是整数,环长度t也是整数,(m / k-1)中,k-1>0,在其他量都确定的情况下,保持(m / k-1)不变的话,分母k-1越小,则分子m也越小,对应快指针在环中走的圈数m也越小,k=2,3,4···,其中k=2时,m最小,即最快相遇,这样效率最高。
环形链表入环点
leetcode142题:https://leetcode.cn/problems/linked-list-cycle-ii/
同样可以推导一下。
快慢指针走得步数:f=2(s+j)
快慢指针相遇时,f=(s+j) +mt(公式含义同最上)
则可以得出s+j=mt,相遇时绕的圈数刚好等于慢指针走的步数。
假设此时再走 l 步到达环的入口,会与走s步的指针相遇,有mt+l=mt+s (环中加mt还是原点)
合并上面两个式子后得 l=s,即再走非环的部分s步即可到入环点。
如图,紫色节点相遇后,假设快指针再绕一圈到这里,走了b+c,而慢指针走到这里,走了a+b,其中b为公共部分,则a=c。
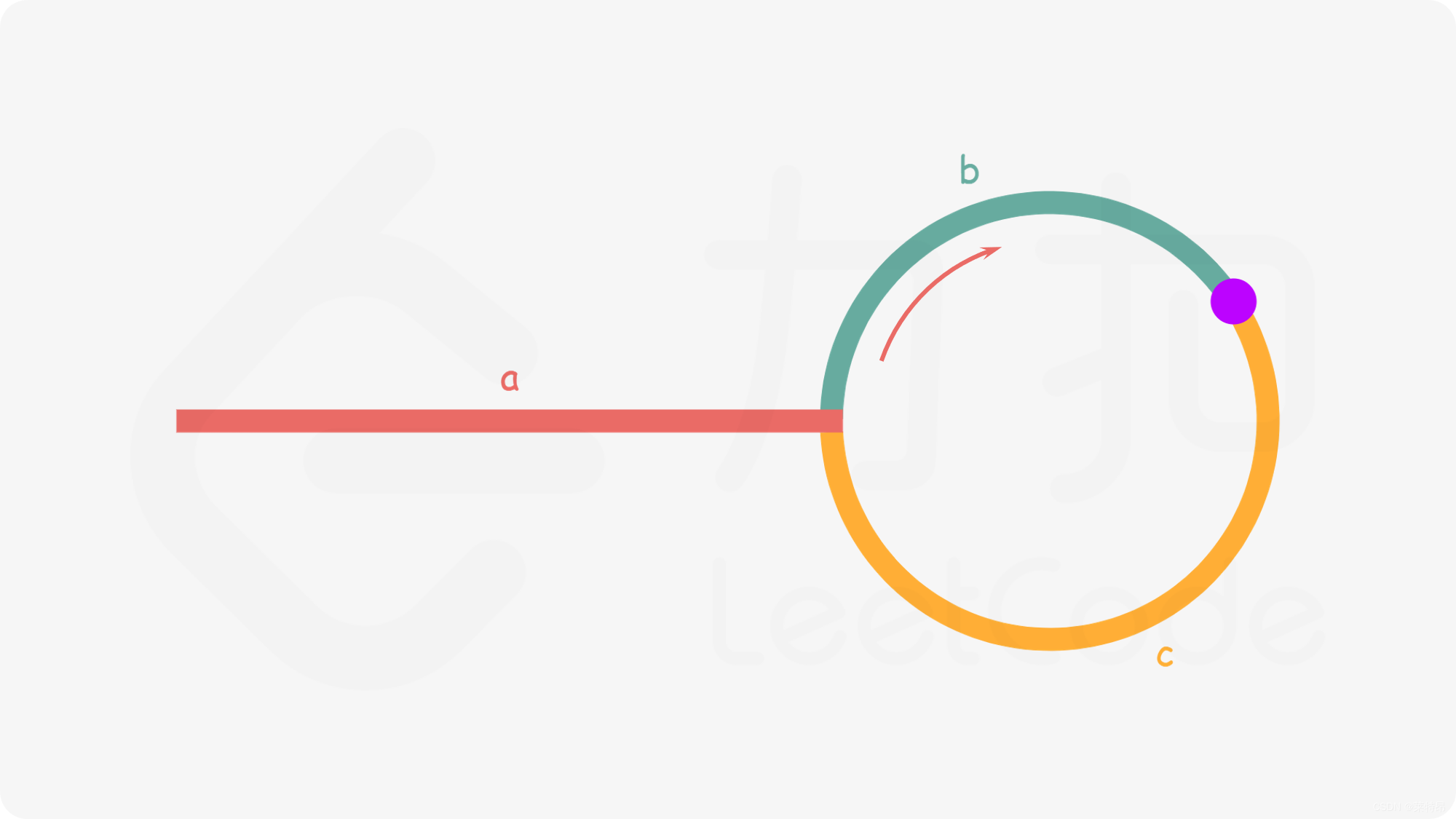
总结:相遇时,慢指针走的步数刚好为快指针在环中绕圈的总步数,距离入环点的步数刚好是非环路径步数。
参考链接:https://stackoverflow.com/questions/5130246/why-increase-pointer-by-two-while-finding-loop-in-linked-list-why-not-3-4-5