1.直接插入排序算法
与打扑克牌类似,将要排序的牌(元素)不断地加入到已排序的牌(元素)中去。把要排序的数组分为了两个部分,一部分是排序好的元素,另一部分是待插入的元素,如果选择的元素比已排序好的元素小,则交换,直到全部元素都比较过为止。
每一次排序相当于一次反向冒泡
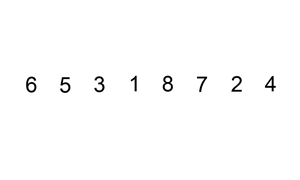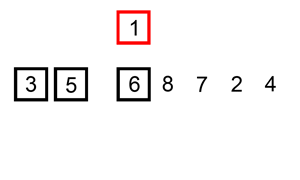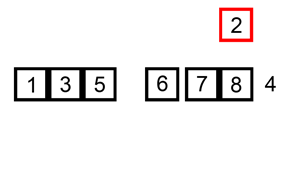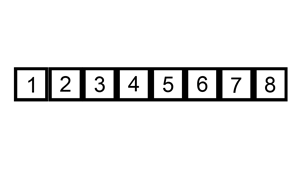
具体代码:
import java.lang.reflect.Array;
import java.util.Arrays;
public class Solution {
public static void main(String[] args) {
InsertSort(new int[] { 9 ,20 , 10, 13 , 12});
}
public static void InsertSort(int [] arr){
int value;//待插入元素
int index;//初始值为待插入元素前一个元素的索引
for(int i= 1 ; i< arr.length;i++){
//i从第二个元素开始,默认第一个元素是有序的
//循环条件是小于数组长度,因为也要将最后一个元素插入到前面的序列
value = arr[i];
index = i - 1;//初始为前一个元素
while(index >=0 && value < arr[index]){
//需要保证index合法
//每当前面的元素比待插入元素大,就向后移动
arr[index + 1] = arr[index];
//不用怕覆盖,因为value保存着待插入的值
index--;
}
//跳出循环条件:index=-1或value>=arr[index]
//因此 选择在此时index右边插入元素
arr[index + 1] = value;
}
System.out.println(Arrays.toString(arr));
}
}时间复杂度:
最优为O(n),比如原数组已经是有序数组了,此时每个元素只需要跟前面一个元素比较一次,共比较n-1次。最差为O(n2),即第i个元素都要与前面共i-1个元素比较。可以认为直接插入排序时间复杂度为O(n2)。
空间复杂度为O(1)
?2.希尔排序
希尔排序算法是直接插入算法的一种改进,其基本思想为按步长先将数据进行分组,对每个组进行直接插入排序,而后减小步长,重复分组+排序,直到步长为1。

import java.util.Arrays;
public class ShellSort {
public static void sort(int[] a){
//确定初始的步长
int h = 1;
while(h<a.length/2){
h = h*2+1;
}//h=7
while(h>=1){//h=7,3,1
//i用于确定分组的起点
for(int i = h;i<a.length;i++){
//从后往前分组
for(int j = i;j>=h;j-=h){
//步长不同的插入排序
if(a[j-h]>a[j]){
int temp = a[j-h];
a[j-h] = a[j];
a[j] = temp;
}else{
break;
}
}
}
//减小步长
h/=2;
}
}
public static void main(String[] args) {
int[] a = {9,5,8,2,4,1,3,7,6};
sort(a);
System.out.println(Arrays.toString(a));
}
}
?例子来源
时间复杂度:取决于步长,假设以N/2作为起始步长,则最坏情况为O(N2)。
空间复杂度:O(1)
3.归并排序
归并排序是分治思想的体现,其思路是将数组拆分成子数组直到每个数组只有一个元素,而后再将数组两两合并,直到合并成为一个数组。

public static void sort(int[] a,int left,int right){
if(right>=left)return; //当子数组长度为1时退出
int mid = (right+left)/2;
sort(int[] a,left,mid);
sort(int[] a,mid+1;right);
merge(int[] a,left,mid,right);
}
public static void merge(int[]a,int left,int mid,int right){
int i = left;
int p1 = left;
int p2 = mid+1;
int[] temp = new int[a.length];
//三个指针 两个数组哪个元素小就放入temp数组
while(p1<=mid&&p2<=right){
if(a[p1]<a[p2]){
temp[i++]=a[p1++];
}else{
temp[i++]=a[p2++];
}
//跳出循环时肯定有一个数组没有放完
while(p1<=mid){
temp[i++]=a[p1++];
}
while(p2<=right){
temp[i++]=a[p2++];
}
for(i = left; i <= right; i++) { //把临时数组中的元素存入原数组中
a[i] = temp[i];
}
}空间复杂度: O(NlogN)
时间复杂度: O(N)
4.简单选择排序
类似冒泡排序,每次都将子序列中最小的数放在最前面。
import java.util.Arrays;
public class SelectSort {
public static void sort(int[] a){
//选择的次数,数组长度减一 次
for(int i = 0; i<a.length-1;i++){
//初始化下标为未排序数组的最左边的下标
int min = i;
//依次比较选择最小的数
for(int j = i+1 ; j<a.length ;j++){
if(a[j]<a[min]){
min = j;
}
}
int temp = a[min];
a[min] = a[i];
a[i] = temp;
}
}
public static void main(String[] args) {
int[] a = {1,5,3,2,6,4,9,8,7};
sort(a);
System.out.println(Arrays.toString(a));
}
}
空间复杂度:O(N2)
时间复杂度: O(1)
5.快速排序
快速排序是冒泡排序的一种改进,冒泡排序每次对相邻的两个数比较,比较消耗时间。
思路:运用了迭代和分治的思想,将数组先进行排序,然后再将其划分成小数组,然后重复排序。
排序方式:设左右两个指针和一个基准数(假设第一个元素),右指针从数组末尾开始反向遍历数组,左指针从另一端开始(索引0)。右指针负责寻找比基准数大的数字,找到即停,左指针负责找比基准数小的数字,找到即停,然后交换两指针对应元素的值,当两指针相遇,则该处为基准数要插入的位置。 此时基准数左侧的数组元素全部小于等于基准数,基准数右侧元素全部大于等于基准数。再将数组分为左右两个子数组,重复上述排序。
public class QuickSort {
//arr 需要排序的数组
//low 开始时最左边的索引=0
//high 开始时最右边的索引=arr.length-1
public static void quickSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>high){
return;
}
i=low;#左边哨兵的索引
j=high;#右边哨兵的索引
//temp就是基准位
temp = arr[low];#以最左边为 基准位
//里基准数远的那个指针先动 即右烧饼索引
while (i<j) {
//先看右边,依次往左递减
#先从右往左找一个小于 基准位的数
#当右边的哨兵位置所在的数>基准位的数 时
#继续从右往左找(同时 j 索引-1)
#找到后会跳出 while循环
while (temp<=arr[j]&&i<j) {
j--;
}
//再看左边,依次往右递增
#步骤和上面类似
while (temp>=arr[i]&&i<j) {
i++;
}
//如果满足条件则交换
if (i<j) {
//z、y 都是临时参数,用于存放 左右哨兵 所在位置的数据
z = arr[i];
y = arr[j];
# 左右哨兵 交换数据(互相持有对方的数据)
arr[i] = y;
arr[j] = z;
}
}
//这时 跳出了 “while (i<j) {}” 循环
//说明 i=j 左右在同一位置
//最后将基准为与i和j相等位置的数字交换
arr[low] = arr[i];#或 arr[low] = arr[j];
arr[i] = temp;#或 arr[j] = temp;
//i=j
//这时 左半数组<(i或j所在索引的数)<右半数组
//也就是说(i或j所在索引的数)已经确定排序位置, 所以就不用再排序了,
// 只要用相同的方法 分别处理 左右数组就可以了
//递归调用左半数组
quickSort(arr, low, j-1);
//递归调用右半数组
quickSort(arr, j+1, high);
}
public static void main(String[] args){
int[] arr = {10,7,2,4,7,62,3,4,2,1,8,9,19};
quickSort(arr, 0, arr.length-1);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}时间复杂度:O(NlogN)
空间复杂度: O(1) 并未申请额外的空间,而是在原数组上进行操作。
6.冒泡排序
冒泡排序的思想是,多次遍历数组,每次都将最大的数放在最后。
public static void sort(int[] a){
//需要冒泡的次数
for(int i = 0 ; i<a.length-1 ;i++){
//对未排序数组依次比较,并放在最后。
for(int j = i;j<a.length-i;j++){
if(a[j]>a[j+1]){
int temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
}
时间复杂度:O(N)
空间复杂度:O(1)
7.堆排序
堆:堆可以看做一个完全二叉树的数组形式。堆又分为大顶堆和小顶堆。
- 大顶堆:每个结点的值都大于或等于左右子结点的值。
- 小顶堆:每个结点的值都小于或等于左右子结点的值。
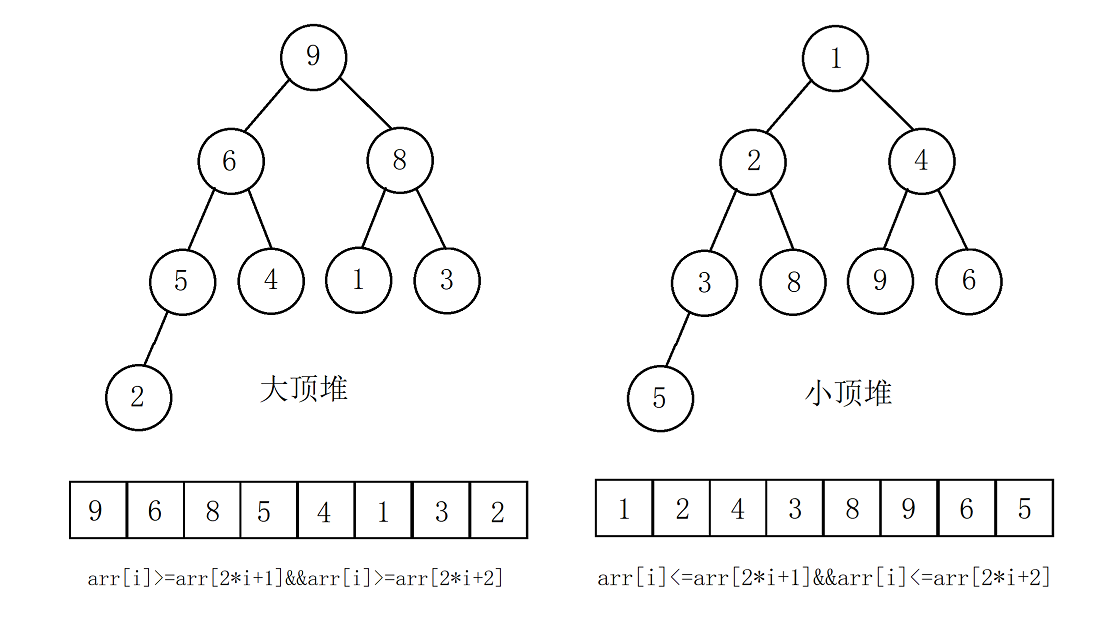
?堆排序的思路:将待排序列构造成一个大顶堆,然后将堆顶元素和数组最后一个元素(arr.length-1)互换,类似于冒泡排序,最大的元素已经被放在最后,再对[0,arr.length-2]的子序列进行排序,不断重复,每一次的堆顶都会被排到子序列的最后位置。大顶堆得到的是升序的排列,小顶堆得到的是降序的排列。
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] array = {4,6,1,2,9,8,3,5};
heapSort(array);
System.out.println(Arrays.toString(array));
}
/**
* 堆排序
*/
public static void heapSort(int[] arr){
//为什么从arr.length/2-1开始?
//因为arr.length/2-1是二叉树最后一个非叶子结点的下标
//第一次排序 从最后一个非叶子结点开始 倒序进行
for (int i = arr.length/2-1; i >= 0 ; i--) {
adjustHeap(arr,i,arr.length);
}
//交换子序列堆顶元素的位置 并对子序列进行排序
for (int j = arr.length-1; j > 0; j--) {
int temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
/*为什么从0开始?
因为在第一次构建大顶堆后让堆顶元素和末尾元素进行交换
而对于其他的非叶子结点所对应的子树都是大顶堆就无需调整,
只需要堆顶元素(下标为0的非叶子结点)的子树调整成大顶堆
*/
adjustHeap(arr,0,j);
}
}
/**
* 构建大顶堆
* 注意:
* 这个方法并不是将整个树调整成大顶堆
* 而是以i对应的非叶子结点的子树调整成大顶堆
* 从i节点往下排序
* @param arr 待调整的数组
* @param i 非叶子结点在数组中的索引(下标)
* @param length 进行调整的元素的个数,length是在逐渐减少的
*/
public static void adjustHeap (int[] arr,int i,int length){
/*取出当前非叶子结点的值保到临时变量中*/
int temp = arr[i];
/*j=i*2+1表示的是i结点的左子结点*/
for (int j = i * 2 + 1; j < length ; j = j * 2 + 1) {
if (j+1 < length && arr[j] < arr[j+1]){ //左子结点小于右子结点
j++; //j指向右子结点
}
if (arr[j] > temp){ //子节点大于父节点
arr[i] = arr[j]; //把较大的值赋值给父节点
//arr[j] = temp; 这里没必要换
i = j; //让i指向与其换位的子结点 因为
}else{
/*子树已经是大顶堆了*/
break;
}
}
arr[i] = temp;
}
}
其实整个排序主要核心就是堆化过程,堆化过程一般是用父节点和他的孩子节点进行比较,取最大的孩子节点和其进行交换;但是要注意这应该是个逆序的,先排序好子树的顺序,然后再一步步往上,到排序根节点上。然后又相反(因为根节点也可能是很小的)的,从根节点往子树上排序。最后才能把所有元素排序好;
?
时间复杂度:O(NlogN)
空间复杂度:O(1) 因为是就地排序,原地更改数组。
8.计数排序
思想:用辅助数组对数组中出现的数字计数,元素转下标,下标转元素。
public static int[] sort ( int[] arr ) {
if (arr.length < 2) {
return arr;
}
int min = arr[0], max = arr[0];
//找出最小值和最大值
for (int i = 0; i < arr.length; i++) {
if (arr[i] < min) {
min = arr[i];
}
if (arr[i] > max) {
max = arr[i];
}
}
//创建辅助数组,数组大小为原数组的最大值
int[] helper = new int[max - min + 1];
for (int e : arr) {
//将原数组的元素作为辅助数组的下标,出现一次次数+1
//e - min计算偏差
helper[e - min]++;
}
//数据回填的位置
int current = 0;
//遍历辅助数组
for (int i = 0; i < helper.length; i++) {
//当前元素出现次数大于1,依次赋给原数组
while (helper[i] > 0) {
//每次赋值后,指针右移
//i + min回填数据计算偏差
arr[current++] = i + min;
helper[i]--;
}
}
return arr;
}
空间复杂度:O(N+M)?其中 M 是原数组的最大值?
时间复杂度:O(N+M)?其中 M 是原数组的最大值(即辅助数组的空间大小)。
由此可见计数排序适用于最大值较小的情况。
9.桶排序
桶排序是计数排序的一种进阶版本。
public static void bucketSort(int[] arr){
// 计算最大值与最小值
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
// 计算桶的数量
int bucketNum = (max - min) / arr.length + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){
bucketArr.add(new ArrayList<Integer>());
}
// 将每个元素放入桶
for(int i = 0; i < arr.length; i++){
int num = (arr[i] - min) / (arr.length);
bucketArr.get(num).add(arr[i]);
}
// 对每个桶进行排序,任意排序方法都可以
for(int i = 0; i < bucketArr.size(); i++){
Collections.sort(bucketArr.get(i));
}
// 将桶中的元素赋值到原序列
int index = 0;
for(int i = 0; i < bucketArr.size(); i++){
for(int j = 0; j < bucketArr.get(i).size(); j++){
arr[index++] = bucketArr.get(i).get(j);
}
}
}
四、复杂度分析
1. 时间复杂度:O(N + C)
对于待排序序列大小为 N,共分为 M 个桶,主要步骤有:
N 次循环,将每个元素装入对应的桶中
M 次循环,对每个桶中的数据进行排序(平均每个桶有 N/M 个元素)
一般使用较为快速的排序算法,时间复杂度为 O ( N l o g N ) O(NlogN)O(NlogN),实际的桶排序过程是以链表形式插入的。
整个桶排序的时间复杂度为:
O ( N ) + O ( M ? ( N / M ? l o g ( N / M ) ) ) = O ( N ? ( l o g ( N / M ) + 1 ) ) O(N)+O(M*(N/M*log(N/M)))=O(N*(log(N/M)+1))O(N)+O(M?(N/M?log(N/M)))=O(N?(log(N/M)+1))
当 N = M 时,复杂度为 O ( N ) O(N)O(N)
2. 额外空间复杂度:O(N + M)
?
桶排序适用场景
桶排序适合外部排序,外部排序就是数据在内存之外,比如磁盘上,数据量比较大,无法 一次性读入内存。
举个例子,假如老板给你一份 10 GB 大小的文件,是订单的交易明细数 据,要求你按订单金额从大到小排序,而你的内存内有 4GB,实际可用内存只有 2 GB, 那么此时就是桶排序发挥作用的时候了。
1. 将文件逐行读入内存(几乎每个编程语言都可 以),扫描并记录最小值,最大值,假如最小值为 1 元,最大值为 10 万元,且都为整数, 不是整数也没关系,可以先乘以 100 换成整数,排序后再除以 100 还原。
?
10.基数排序
基数排序(Radix Sort)是将待排序序列的每个元素统一为同样位数长度的元素,位数较短的通过补0达到长度一致,然后从最低位或从最高位开始,依次进行稳定的计数排序,最终形成有序的序列
基数排序主要是针对整数的排序,由于整数也可以表示字符串或和特定格式的浮点数,因此能用整数表达的其他数据类型也能用基数排序
基数排序既可以从高位优先进行排序(简称MSD),也可以从低位优先进行排序(简称LSD)
public static int[] sort(int[] array) {
if (array.length < 2) return array;
//根据最大值算出位数
int max = array[0];
for (int temp : array) {
if (temp > max) {
max = temp;
}
}
//算出位数digit 比如最大值为120 maxDigit就为2
int maxDigit = 0;
while (max != 0) {
max /= 10;
maxDigit++;
}
//创建桶并初始化
ArrayList<ArrayList<Integer>> bucket = new ArrayList<>();
for (int i = 0; i < 10; i++) {
bucket.add(new ArrayList<>());
}
//按照从右往左的顺序,依次将每一位都当做一次关键字,然后按照该关键字对数组排序,每一轮排序都基于上轮排序后的结果
int mold = 10;//取模运算
int div = 1;//获取对应位数的值
for (int i = 0; i < maxDigit; i++, mold *= 10, div *= 10) {
for (int j = 0; j < array.length; j++) {
//获取个位/十位/百位......
int num = (array[j] % mold) / div;
//把数据放入到对应的桶里
bucket.get(num).add(array[j]);
}
//把桶中的数据重新写回去,并把桶的元素清空,开始第二轮排序
int index = 0;
for (int k = 0; k < bucket.size(); k++) {
//桶中对应的数据
ArrayList<Integer> list = bucket.get(k);
for (int m = 0; m < list.size(); m++) {
array[index++] = list.get(m);
}
//清除桶
bucket.get(k).clear();
}
}
return array;
}时间复杂度:O(k*n),最外层时间复杂度是o(k),k是序列最大数的位数,在里层的出桶时间复杂度是数组的长度O(n),再拼接成数组的时间复杂度平均是数组的长度O(n),总的来说,基数排序的时间复杂度是o(k*(n+n)),即O(k*n)
空间复杂度:O(K+N)
适用于位数不多,每一位范围不大的序列。
附总结:

?