四种算法
dijstra:贪心算法
floyd算法:一部分点位的最短长度
图比较稀疏的时候:kruskal
图比较密的时候:prim
问题:
1.Dijstra我们得到的是什么?
答:得到的是从初始点开始到所有点位的值,包括所有拐点
2.Floyd算法为什么行?这么简单为什么好?计算路径为什么能?
答:对每一个单元长度都进行了拆分,相当于一个接着一个,但是每个小路径长度上都是独立的,做最好的自己
3.为什么最小生成树得到的总权最小?
答:可以看Kruskal算法,是按照路线权值排序得到的最终树,这不小谁小?
4.为什么最短边会出现在最小生成树里面?
答:答案同上
以下是最短路径算法:着眼全局,all_scan
Dijkstra算法:找到一个顶点到所有点的最短路径
(不适用有负权值的图,由于该算法的贪心性质,它“看不到”远处的负权边,所以会破坏松弛操作的正确性(加上负权边之后本来已经确定的最短路径就不再是最短的了)
S ={已经确认收入囊中的最小路径}(在拓展的环节中不更新)
U={尚未收入囊中的点位,初始距离为999}(在拓展的过程中更新
主要实现方案:
1.选择一个开始的点,
2.把这个点最近的一个点记录下来(U中),加入S(为了方便,在这里也可以使用最小堆来进行)
3.从现在这个点开始,环顾周围所有尚未加入S的点,计算从这里开始能否将到达U中点位的距离更新为最短,若更新,一同记录下现在的拐点(1.这个记录是从开始的点来此处的最短距离 2.记录了前一个转弯点)。
重复2.3两步,直到把所有的都囊括在内
问:为什么只需要更新U?
答:因为直接更新S意义不大,作为一个由贪心算法演变而来的算法,Dijkstra的最开始的每一步都是选择了最棒的路径,之前的不会存在更大
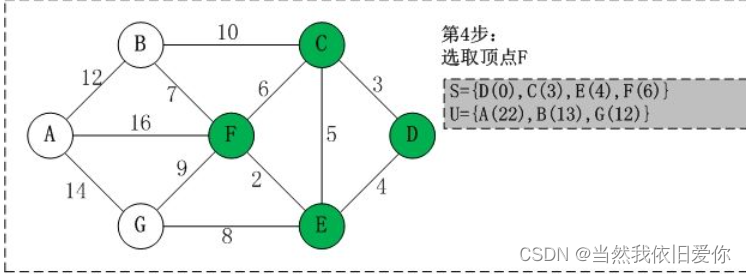
👇下图这里V代表了顶点数,E代表了所有边
方法二最后的等号后的表达不是很准确,如果是连通图的话,E比V大,这样写比较好,否则就不要这样写。之所以是加,是因为这是两个不同的操作

算法实现:
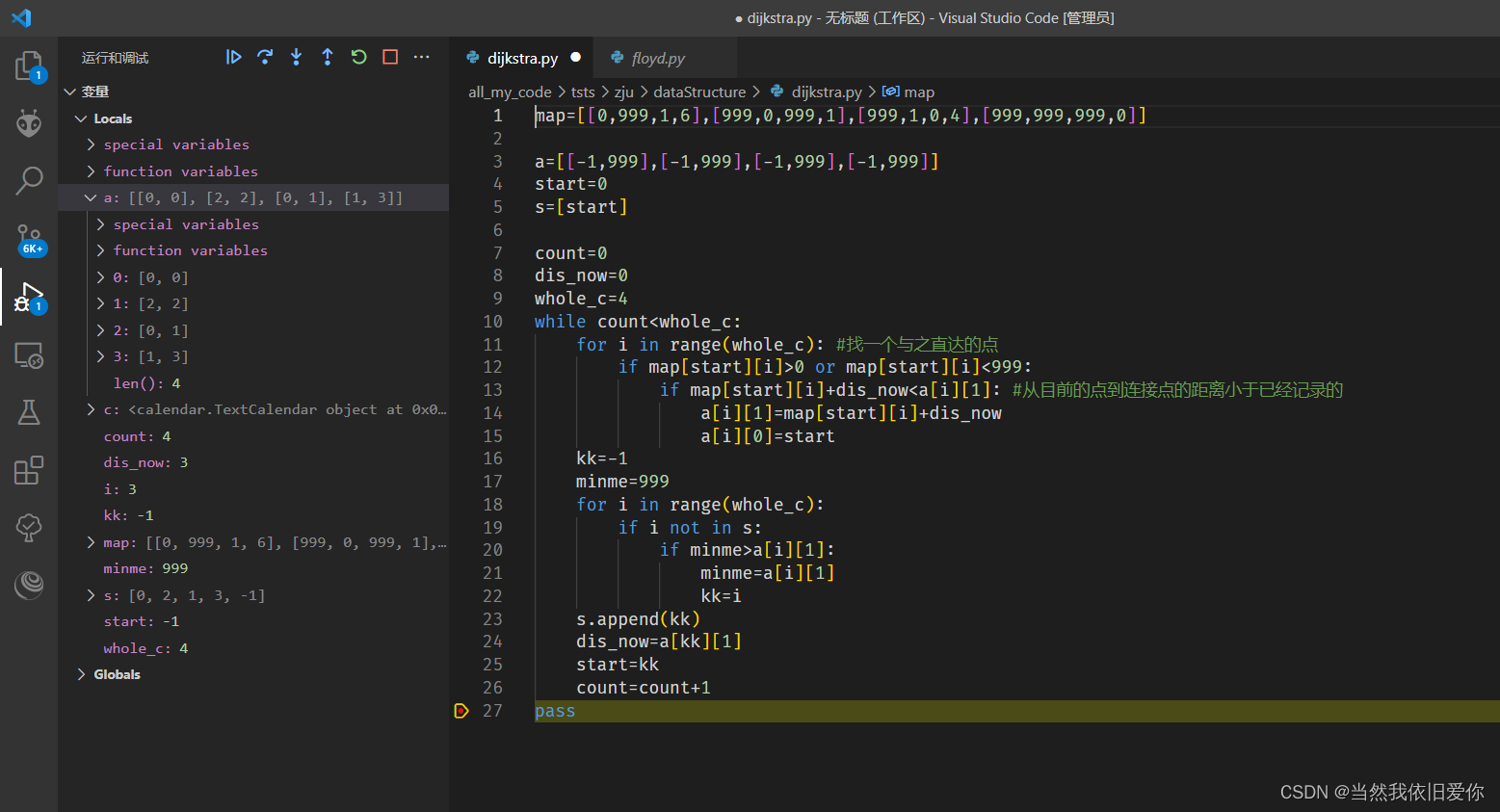
最后得到的是一个地图a:其中的值是:(转弯点,开始到此处的路长)
map=[[0,999,1,6],[999,0,999,1],[999,1,0,4],[999,999,999,0]]
a=[[-1,999],[-1,999],[-1,999],[-1,999]]
start=0
s=[start]
count=0
dis_now=0
whole_c=4
while count<whole_c:
for i in range(whole_c): #找一个与之直达的点
if map[start][i]>0 or map[start][i]<999:
if map[start][i]+dis_now<a[i][1]: #从目前的点到连接点的距离小于已经记录的
a[i][1]=map[start][i]+dis_now
a[i][0]=start
kk=-1
minme=999
for i in range(whole_c):
if i not in s:
if minme>a[i][1]:
minme=a[i][1]
kk=i
s.append(kk)
dis_now=a[kk][1]
start=kk
count=count+1
pass
2.Floyd算法:
佛洛依德算法:将一个a[i][j]分解为:a[i][x]+a[x][j],这就代表了如果我想要实现一条从金华到杭州的路线,我的办法是:看各条路线是否能被拆分为一条一条最短的路线,能否变成从金华到绍兴,绍兴到杭州的路线.通过对一个矩阵中的所有路线进行循环
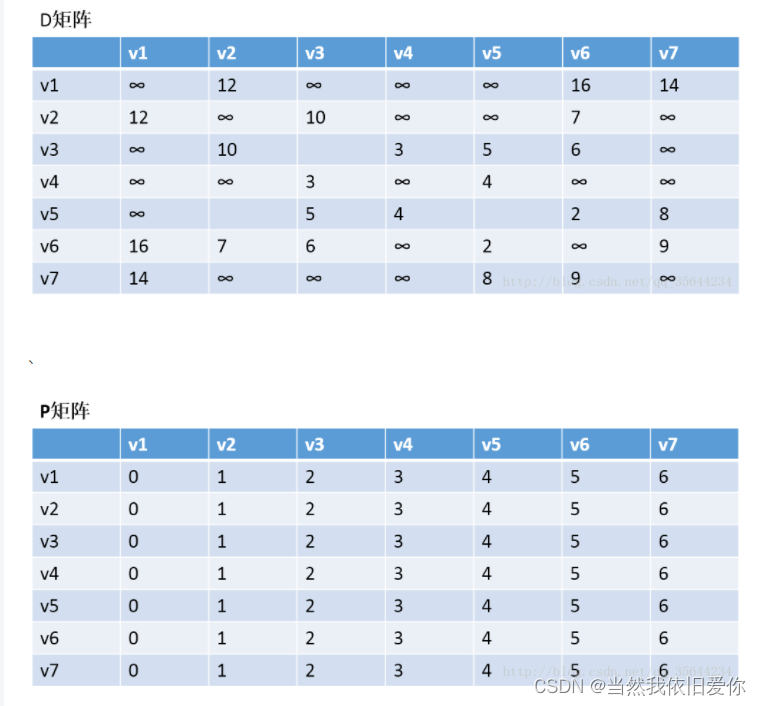
在这里我定义了两个矩阵,一个矩阵是代表了距离,另外一个是代表从某个点到某个点我应当到那里中转。
我如果不知道到这个地方要多远,就将初始值设置为正无穷,自己到自己的序号就是自己
所以最后我会得到两个矩阵,一个代表了从某个点到某个点的距离
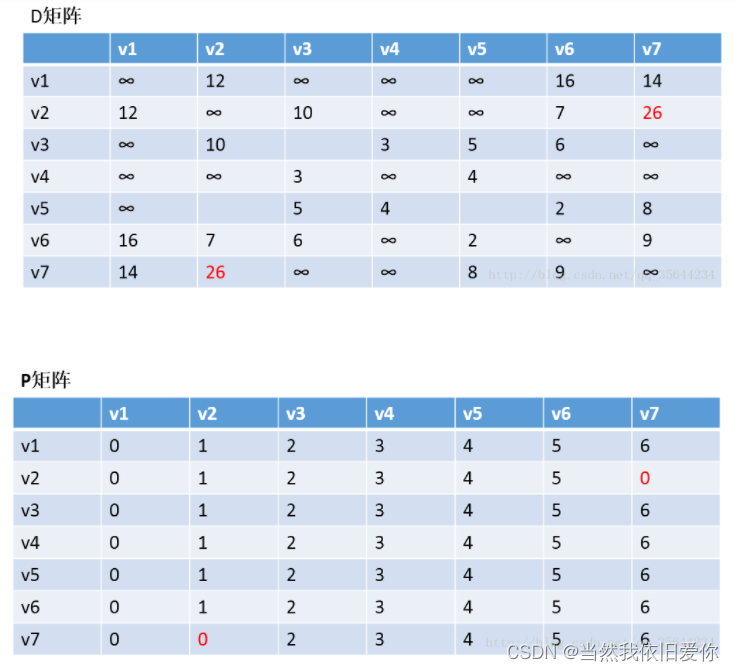
(这个图只是中途的)
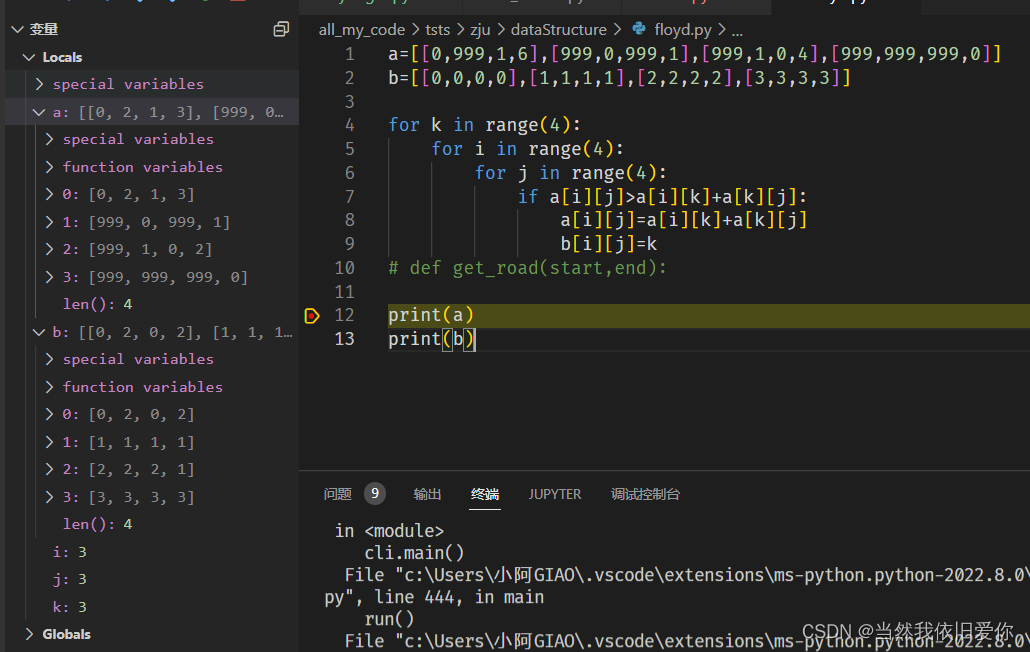
代码实现:
a=[[0,999,1,6],[999,0,999,1],[999,1,0,4],[999,999,999,0]]
b=[[0,0,0,0],[1,1,1,1],[2,2,2,2],[3,3,3,3]]
for k in range(4):
for i in range(4):
for j in range(4):
if a[i][j]>a[i][k]+a[k][j]:
a[i][j]=a[i][k]+a[k][j]
b[i][j]=k
# def get_road(start,end):
print(a)
print(b)
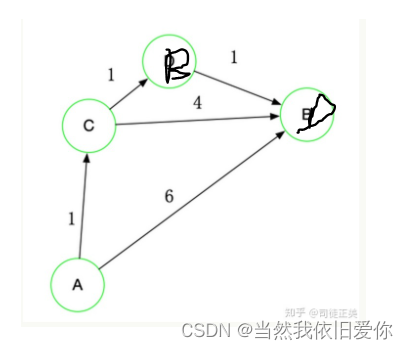
怎么让A到B,检查A到B的矩阵b[0][1]==2,现在把起始点保存为2(即为C),问题转化为C到D,再次检查,转化为B到D,最后得到答案
以下的都是最小生成树算法(只着眼于当下,最小生成树的总权最小,不是其中两点的任意路径最小;)
3.prim算法:
1.找到一个点,放入集合S
2.对这个这个点周围的所有线进行排序,然后连上最短的,把这个连上的点放入集合S
3.对S中所有的点的线进行排序
4.继续加入,但是要保证加上的点并不存在于已经有的树中
4.Kruskal算法
对长边进行排序,如果没有形成环路,就将所有不同长度地边进行排序,然后一个又一个地连在一起
只要满足:连线之间没有形成环路,就可以不断的连在一起(这里可以使用并差集)
判断环路的两个方法:
1.两个点不在同一颗树中,并查集法
2.连接的最大点不是相同的,终点法(老师没讲,这个暂时还没看懂)
直到所有点都被包含为止