目录
系列文章目录
刷题笔记(一)–数组类型:二分法
刷题笔记(二)–数组类型:双指针法
刷题笔记(三)–数组类型:滑动窗口
刷题笔记(四)–数组类型:模拟
刷题笔记(五)–链表类型:基础题目以及操作
刷题笔记(六)–哈希表:基础题目和思想
刷题笔记(七)–字符串:经典题目
刷题笔记(八)–双指针:两数之和以及延伸
刷题笔记(九)–字符串:KMP算法
刷题笔记(十)–栈和队列:基础题目
刷题笔记(十一)–栈和队列:Top-K问题
刷题笔记(十二)–复习:排序算法
刷题笔记(十三)–二叉树:前中后序遍历(复习)
刷题笔记(十四)–二叉树:层序遍历和DFS,BFS
刷题笔记(十五)–二叉树:属性相关题目
刷题笔记(十六)–二叉树:修改与构造
刷题笔记(十七)–二叉搜索树:关于属性问题
刷题笔记(十八)–二叉树:公共祖先问题
前言
二叉树最后一篇博客啦!!!下篇就是回溯算法!!搞起!
题录
701. 二叉搜索树中的插入操作
题目链接如下:
题目截图如下:
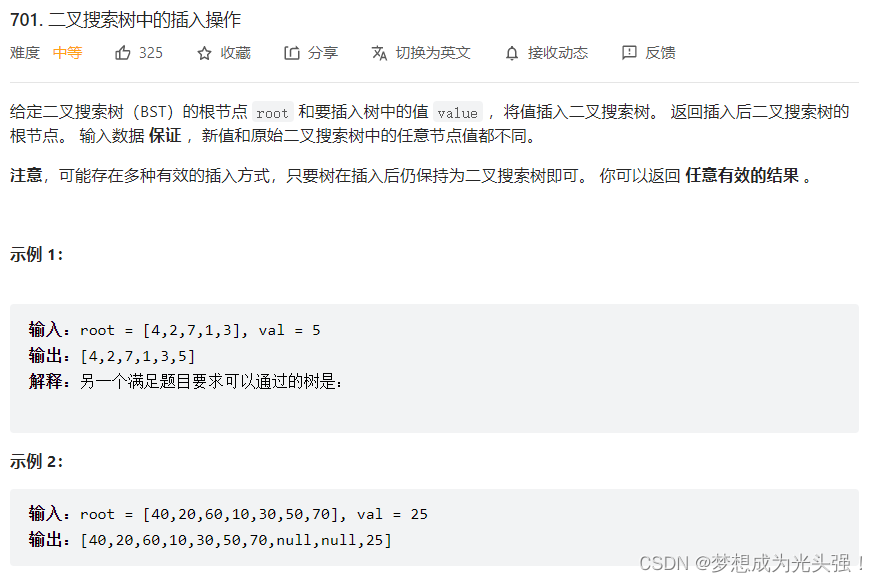
二叉搜索树这里的题一定要注意很重要的一个技巧,就是它的后序遍历,因为二叉搜索树后序遍历的特殊性,所以很多时候题目都是根据后序遍历来进行演变。
递归_DFS
public class 二叉搜索树中的插入操作 {
public TreeNode insertIntoBST(TreeNode root, int val) {
//如果说当前节点已经为空了就走到了最底层,此时直接构造一个新的节点就可以
if(root == null) return new TreeNode(val);
//判断当前节点的值和左右子树之间的关系,从而决定下一步的走向
if(root.val > val){
root.left = insertIntoBST(root.left,val);
}else{
root.right = insertIntoBST(root.right,val);
}
return root;
}
}
迭代_BFS
二叉树的插入操作怎么说呢,其实就是一个不断遍历的过程。但是在这个遍历的过程中,要保存两个节点的值,也就是当前节点和上一个节点的值。
public class 二叉搜索树中的插入操作_迭代写法 {
public TreeNode insertIntoBST(TreeNode root, int val) {
if(root == null) return new TreeNode(val);
//定义两个节点指针,用来进行当前节点和上一个节点的保存
TreeNode parent = root,key = root;
while(key != null){
parent = key;
key = key.val < val ? key.right : key.left;
}
//注意哈,这里如果说插入节点的值等于当前节点的话,会把当前节点的值进行覆盖
if(parent.val > val) parent.left = new TreeNode(val);
else if(parent.val < val) parent.right = new TreeNode(val);
return root;
}
}
450. 删除二叉搜索树中的节点
题目链接如下:
题目截图如下:
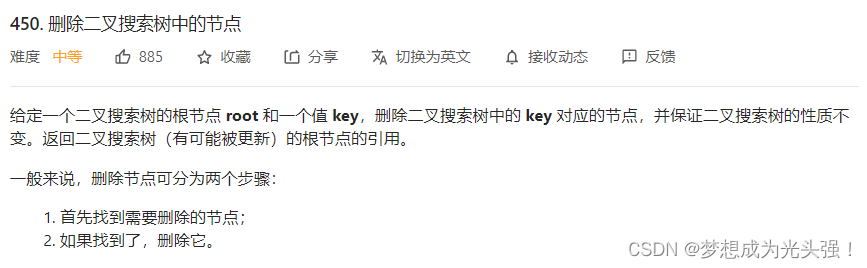
这个题目呢,大致可以分为以下几步
1.找到待删除节点
2.对待删除节点进行分类
<1>待删除节点为叶子结点
<2>待删除节点左子树为空
<3>待删除节点右子树为空
<4>待删除节点的左右子树健全
3.删除对应节点
具体代码如下:
public class 二叉搜索树中的删除操作 {
public TreeNode deleteNode(TreeNode root, int key) {
TreeNode cur = root;//当前指针
TreeNode parent = null;//记录上一个遍历的节点
//找到待删除节点
while(cur != null){
if(cur.val > key){
parent = cur;
cur = cur.left;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else{
break;
}
}
if(cur == null) return root;//如果说没有找到待删除的节点,那么就返回根节点就好(这里也包含了测试用例为[]的情况)
if(cur.left == null){//1.左子树为空(可能为根节点) 同时处理
if(parent == null){//这里添加这种情况的识别是因为待删除节点可能是根节点
root = cur.right;
}else{
if(parent.left == cur) parent.left = cur.right;
else parent.right = cur.right;
}
cur.right = null;
}
else if(cur.right == null){//2.右子树为空(可能为根节点)
if(parent == null){//这里添加这种情况的识别是因为待删除节点可能是根节点
root = cur.left;
}else {
if (parent.left == cur) parent.left = cur.left;
else parent.right = cur.left;
}
cur.left = null;
}
else{//这就是最后一种情况了,就是当前节点的左右子树都在,这种的比较特殊,这里的删除要换一种形式
//这种删除就是找一个合适的节点值进行覆盖
parent = cur;
TreeNode fac = cur.right;//这个节点用来找左子树的最大值或者说右子树的最小值
//一般情况我们的选择就是右子树的最小值
while(fac.left != null){
parent = fac;
fac = fac.left;
}
//找到后覆盖当前待删除节点
cur.val = fac.val;
if(parent.left == fac){//如果找到的节点是父节点的左子树
parent.left = fac.right;
}else{//如果找到的节点为父节点的右子树
parent.right = fac.right;
}
}
return root;
}
}
669. 修剪二叉搜索树
题目链接如下:
题目截图如下:
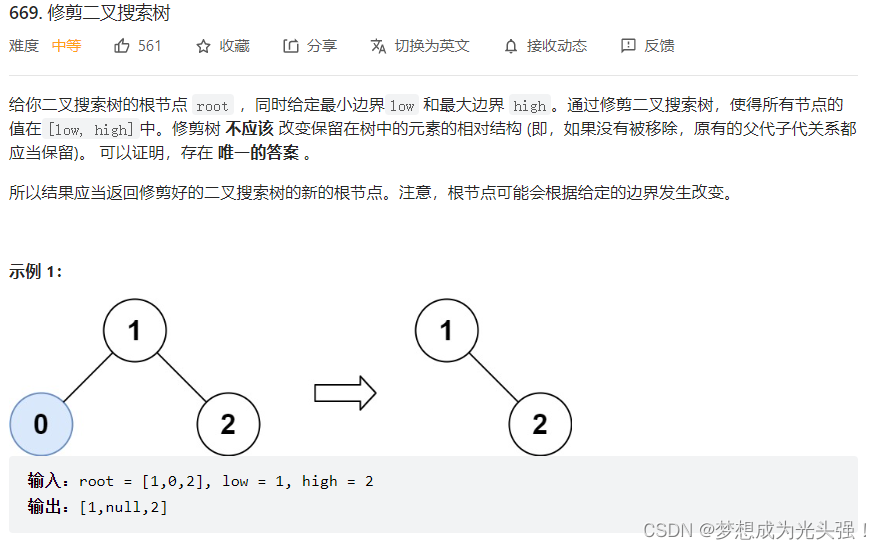
这里的修剪其实咋说呢,虽然说是一个简单题,但是修剪的过程其实还是挺折磨人的。
public class 修剪二叉搜索树 {
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root == null) return null;
//然后就是后序遍历,先是遍历左右子树
root.left = trimBST(root.left,low,high);
root.right = trimBST(root.right,low,high);
//然后对当前树根节点下手
//如果说根节点不符合要求,那就去对左右子树处理
if(root.val < low) return trimBST(root.right,low,high);
if(root.val > high) return trimBST(root.left,low,high);
return root;
}
}
108. 将有序数组转换为二叉搜索树
题目链接如下:
题目截图如下:
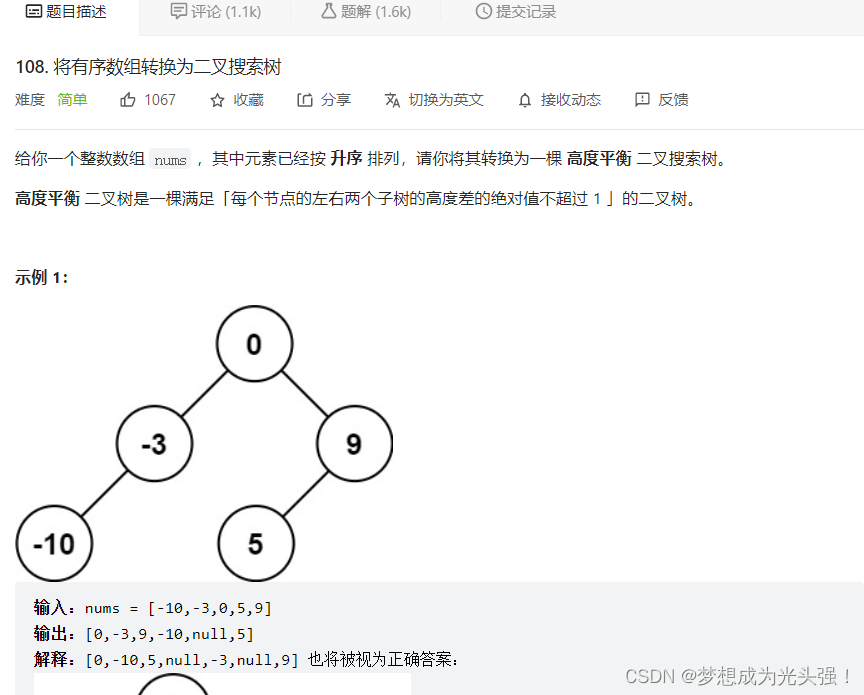
public class 将有序数组转为二叉搜索树 {
public TreeNode sortedArrayToBST(int[] nums) {
if(nums.length == 0) return null;
return solve(nums,0, nums.length);
}
//其实不是很复杂,因为和构建普通的二叉树没有啥区别,因为它的取值是很固定的,一直是从中间取的。
public TreeNode solve(int[] nums,int left,int right){
//如果说left > right就直接返回一个null节点就行
if(left >= right) return null;
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = solve(nums,left,mid);
root.right = solve(nums,mid + 1,right);
return root;
}
}
538. 把二叉搜索树转换为累加树
题目链接如下:
题目截图如下:
这道题虽然是中等题,但是其实不是很难。我们的中序遍历是左子树>>根节点>>右子树,但是这里需要的遍历方式是右子树>>根节点>>左子树,所以调换一下顺序就好了。
public class 二叉搜索树转化为累加树 {
int num;
public TreeNode convertBST(TreeNode root) {
if(root == null) return null;
solve(root);
return root;
}
public void solve(TreeNode root){
if(root == null) return;
solve(root.right);
root.val += num;
num = root.val;
solve(root.left);
}
}