[数据结构与算法]【密码学】分组密码算法的工作模式（9）——分组链接工作模式

12 分组链接工作模式

12.1 变量定义

BC工作模式采用以下变量。
a）输入变量：
??????1）$q$个明文分组$P_1,P_2,...,P_q$所组成的序列，每个分组都为$n$比特；
??????2）密钥$K$，需要加解密操作方约定一致，长度由分组密码算法$E$决定；
??????3）初始向量$IV$，需要加解密操作方约定一致，长度为$n$比特。
b）中间变量：
??????$q$个反馈变量$F_1,F_2,...,F_q$所组成的序列，每个变量都为$n$比特。
c）输出变量：
??????$q$个密文分组$C_1,C_2,...,C_q$所组成的序列，每个分组都为$n$比特。

12.2 BC的加密方式描述

设置反馈变量初始向量：$F_1=IV$。
加密运算按照如下两个步骤进行：
a）生成密文分组：$C_i=E_k(P_i\oplus F_i)$；
b）生成反馈变量：$F_{i+1}=F_i\oplus C_i$。
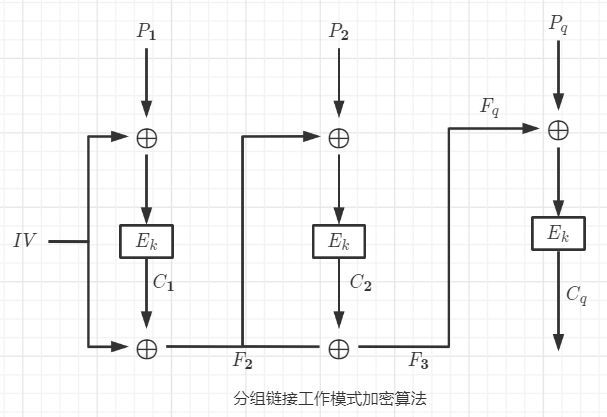
对$i=1,2,...,q$，重复上述步骤，最后一个循环结束于a）。此过程如下图所示。初始向量$IV$用于生成第一个密文输出。之后的加密过程中，每个密文与当时反馈变量进行异或运算，生成下一个反馈变量。

12.3 BC的加密方式示例

本示例使用的分组密码是GB/T 32907——2016中规定的SM4算法。所有变量采用“左高右低”的方式标记，即变量最左侧为其最高位。
密钥密钥为（十六进制）：2B7E1516 28AED2A6 ABF71588 09CF4F3C。
初始向量为（十六进制）：00010203 04050607 08090A0B 0C0D0E0F。
明文是（十六进制）：6BC1BEE2 2E409F96 E93D7E11 7393172A
????????????????????????????????????AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
????????????????????????????????????30C81C46 A35CE411 E5FBC119 1A0A52EF
????????????????????????????????????F69F2445 DF4F9B17 AD2B417B E66C3710。


$i=1$时：
$F_1=IV=$ 00010203 04050607 08090A0B 0C0D0E0F
$P_1\oplus F_1=$ (6BC1BEE2 2E409F96 E93D7E11 7393172A) $\oplus$ (00010203 04050607 08090A0B 0C0D0E0F) $=$ 6BC0BCE1 2A459991 E134741A 7F9E1925
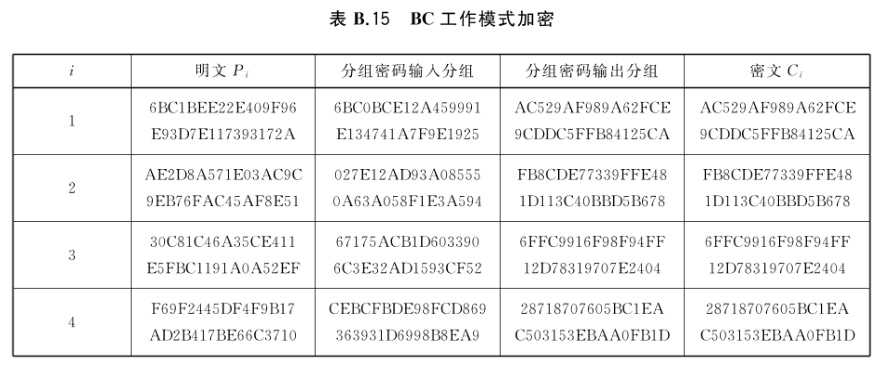
a）$C_1=E_k(P_1\oplus F_1)=$ AC529AF9 89A62FCE 9CDDC5FF B84125CA
b）$F_2=F_1\oplus C_1=$ (00010203 04050607 08090A0B 0C0D0E0F) $\oplus$ (AC529AF9 89A62FCE 9CDDC5FF B84125CA) = AC5398FA 8DA329C9 94D4CFF4 B44C2BC5


$i=2$时：
$P_2\oplus F_2=$ (AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51) $\oplus$ (AC5398FA 8DA329C9 94D4CFF4 B44C2BC5) $=$ 027E12AD 93A08555 0A63A058 F1E3A594
a）$C_2=E_k(P_2\oplus F_2)=$ FB8CDE77 339FFE48 1D113C40 BBD5B678
b）$F_3=F_2\oplus C_2=$ (AC5398FA 8DA329C9 94D4CFF4 B44C2BC5) $\oplus$ (FB8CDE77 339FFE48 1D113C40 BBD5B678) $=$ 57DF468D BE3CD781 89C5F3B4 0F999DBD


$i=3$时：
$P_3\oplus F_3=$ (30C81C46 A35CE411 E5FBC119 1A0A52EF) $\oplus$ (57DF468D BE3CD781 89C5F3B4 0F999DBD) $=$ 67175ACB 1D603390 6C3E32AD 1593CF52
a）$C_3=E_k(P_3\oplus F_3)=$ 6FFC9916 F98F94FF 12D78319 707E2404
b）$F_4=F_3\oplus C_3=$ (57DF468D BE3CD781 89C5F3B4 0F999DBD) $\oplus$ (6FFC9916 F98F94FF 12D78319 707E2404) $=$ 3823DF9B 47B3437E 9B1270AD 7FE7B9B9


$i=4$时：
$P_4\oplus F_4=$ (F69F2445 DF4F9B17 AD2B417B E66C3710) $\oplus$ (3823DF9B 47B3437E 9B1270AD 7FE7B9B9) $=$ CEBCFBDE 98FCD869 363931D6 998B8EA9
a）$C_4=E_k(P_4\oplus F_4)=$ 28718707 605BC1EA C503153E BAA0FB1D

12.4 BC的解密方式描述

设置反馈变量初始向量：$F_1=IV$。
解密运算按照如下两个步骤进行：
a）生成明文分组：$P_i=F_i\oplus D_k(C_i)$；
b）生成反馈变量：$F_{i+1}=F_i\oplus C_i$。
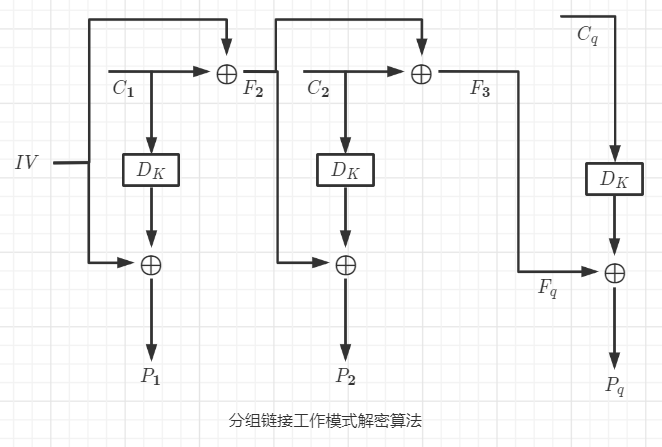
对$i=1,2,...,q$，重复上述步骤，最后一个循环结束于a）。此过程如下图所示。

12.5 BC的解密方式示例

本示例使用的分组密码是GB/T 32907——2016中规定的SM4算法。所有变量采用“左高右低”的方式标记，即变量最左侧为其最高位。
密钥密钥为（十六进制）：2B7E1516 28AED2A6 ABF71588 09CF4F3C。
初始向量为（十六进制）：00010203 04050607 08090A0B 0C0D0E0F。
密文是（十六进制）：AC529AF9 89A62FCE 9CDDC5FF B84125CA
????????????????????????????????????FB8CDE77 339FFE48 1D113C40 BBD5B678
????????????????????????????????????6FFC9916 F98F94FF 12D78319 707E2404
????????????????????????????????????28718707 605BC1EA C503153E BAA0FB1D。


$i=1$时：
$F_1=IV=$ 00010203 04050607 08090A0B 0C0D0E0F
$D_k(C_1)=$ 6BC0BCE1 2A459991 E134741A 7F9E1925
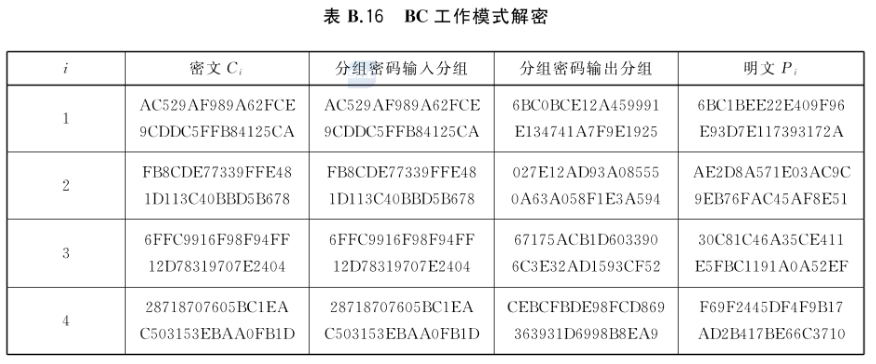
a）$P_1=F_1\oplus D_k(C_1)=$ (00010203 04050607 08090A0B 0C0D0E0F) $\oplus$ (6BC0BCE1 2A459991 E134741A 7F9E1925) $=$ 6BC1BEE2 2E409F96 E93D7E11 7393172A
b）$F_2=F_1\oplus C_1=$ (00010203 04050607 08090A0B 0C0D0E0F) $\oplus$ (AC529AF9 89A62FCE 9CDDC5FF B84125CA) $=$ AC5398FA 8DA329C9 94D4CFF4 B44C2BC5


$i=2$时：
$D_k(C_2)=$ 027E12AD 93A08555 0A63A058 F1E3A594
a）$P_2=F_2\oplus D_k(C_2)=$ (AC5398FA 8DA329C9 94D4CFF4 B44C2BC5) $\oplus$ (027E12AD 93A08555 0A63A058 F1E3A594) $=$ AE2D8A57 1E03AC9C 9EB76FAC 45AF8E51
b）$F_3=F_2\oplus C_2=$ (AC5398FA 8DA329C9 94D4CFF4 B44C2BC5) $\oplus$ (FB8CDE77 339FFE48 1D113C40 BBD5B678) $=$ 57DF468D BE3CD781 89C5F3B4 0F999DBD


$i=3$时：
$D_k(C_3)=$ 67175ACB 1D603390 6C3E32AD 1593CF52
a）$P_3=F_3\oplus D_k(C_3)=$ (57DF468D BE3CD781 89C5F3B4 0F999DBD) $\oplus$ (67175ACB 1D603390 6C3E32AD 1593CF52) $=$ 30C81C46 A35CE411 E5FBC119 1A0A52EF
b）$F_4=F_3\oplus C_3=$ (57DF468D BE3CD781 89C5F3B4 0F999DBD) $\oplus$ (6FFC9916 F98F94FF 12D78319 707E2404) $=$ 3823DF9B 47B3437E 9B1270AD 7FE7B9B9


$i=4$时：
$D_k(C_4)=$ CEBCFBDE 98FCD869 363931D6 998B8EA9
$P_4=F_4\oplus D_k(C_4)=$ (3823DF9B 47B3437E 9B1270AD 7FE7B9B9) $\oplus$ (CEBCFBDE 98FCD869 363931D6 998B8EA9) $=$ F69F2445 DF4F9B17 AD2B417B E66C3710

12.6 分组链接工作模式的性质

12.6.1 场景

为了在分组链接模式中使用分组算法，可以简单地将分组密码算法的输入跟所有前面密文分组的异或值相异或。如CBC算法，过程要从一个初始向量$IV$开始。
只要使用同样的密钥和初始向量对相同的明文进行加密，BC工作模式将生成相同的密文。介意这种性质的用户需要采用某种方法来改变初始明文分组、密钥或初始向量。

12.6.2 性质

BC工作模式的性质有：
a）链接操作使得密文分组依赖于当前的和以前的明文分组，因此对密文分组的重新排序不会导致对相应明文分组的重新排序；
b）使用不同的$IV$从而防止同一明文加密成同一密文；

12.6.3 填充明文

只有长度为分组长度整数倍的明文才能被加密，其他长度的明文需要被填充至分组长度的整数倍。

12.6.4 差错扩散

BC模式的反馈过程具有扩散明文错误的性质，这个问题是由于密文分组的解密依赖于所有前面的密文分组，密文中任一错误都将导致所有后续密文分组的解密出错。

12.6.5 同步

如果解密或解密之间的分组边界丢失了（例如由于一个比特的滑动），则在重新建立正确的分组边界之前加密与解密之间将失去同步。如果分组边界丢失，所有解密操作的结果都是不正确的。