一、前、中、后缀表达式定义
一般我们常用的中缀表达式,中缀表达式不仅依靠运算符的优先级,也要处理括号的优先级;后缀表达式中没有括号,只有操作数和运算符,且运算符放在操作数的后面;前缀表达式也是一种没有括号的算术表达式,其运算符写在前面,操作数写在后面。
将常用的中缀表达式转换为前缀表达式、后缀表达式后,可以通过栈的相关原理来实现具体的出栈 、入栈操作逻辑,从而可以一样完成与中缀表达式相同的运算。
二、具体转换步骤
(一)中缀表达式转换为前缀表达式
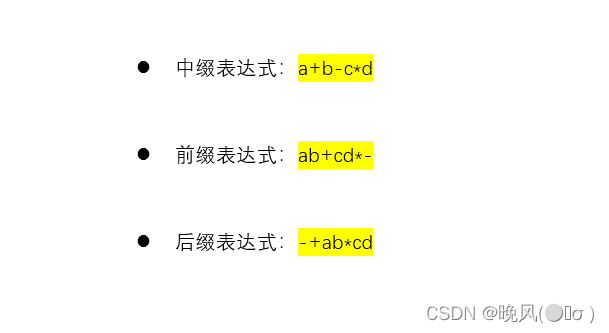
以a+b-c*d为例,将中缀表达式转换为前缀表达式。
1、首先按照运算优先级将所有的操作数都加上括号。

2、将运算符移至相对应的括号前。

3、将括号去掉,即可得到前缀表达式。

(二)中缀表达式转换为后缀表达式
与前缀表达式相反,第二步将运算符移至相对应的括号后,然后再去掉括号,如下图:

这里以中缀表达式转换为后缀表达式,简单讲解具体的栈的实现方法:
1、将一个中缀表达式转换为后缀表达式,首先从左到右扫描整个中缀表达式,当遇到操作数时加入至待定的后缀表达式区域中(这是一个栈);
2、遇到操作符时,若为’(‘,则入栈,若为’)',则依次将栈中的运算符加入至后缀表达式的栈中,直到出现‘(’后,从栈中删除‘(’;
3、遇到运算符时,当为比括号优先级高的优先级时,直接入栈,否则,依次从栈中弹出比当前运算符优先级高和优先级相等的运算符,直到遇到比它优先级低或者遇到一个‘(’为止;
4、当扫描完结束后,栈中的所有运算符依次出栈加入后缀表达式。
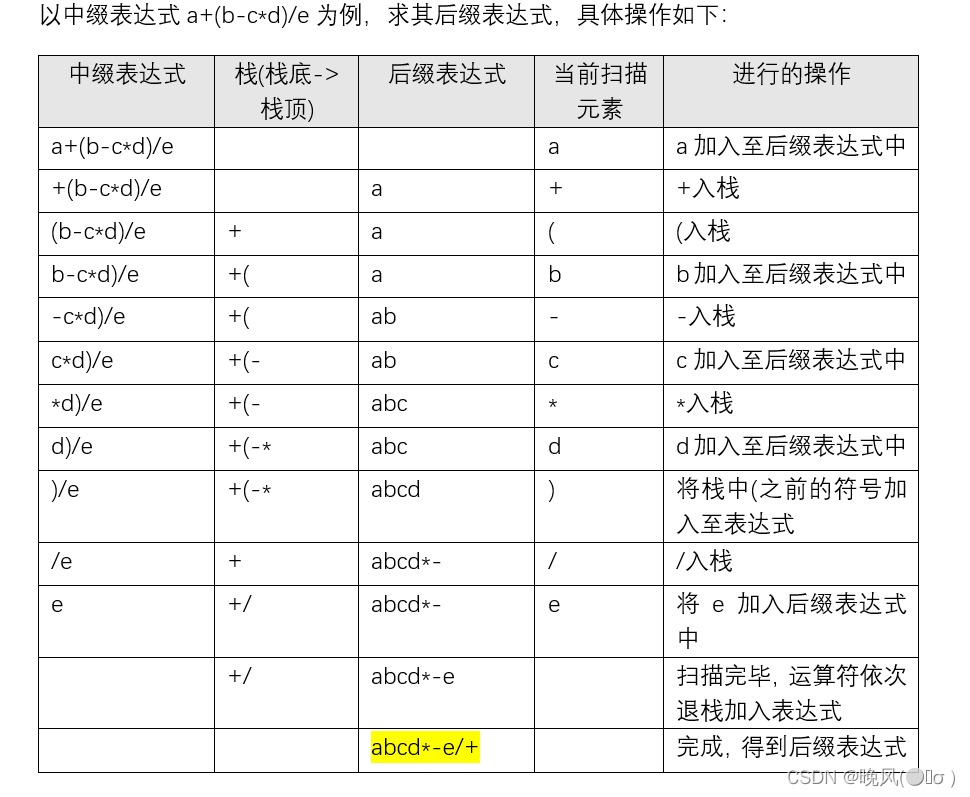
通过手工算,第一步转换为(a+((b-(c*d))/e)),第二步提运算符转为(a((b(cd)*)-e)/)+,去掉括号得到后缀表达式abcd*-e/+。
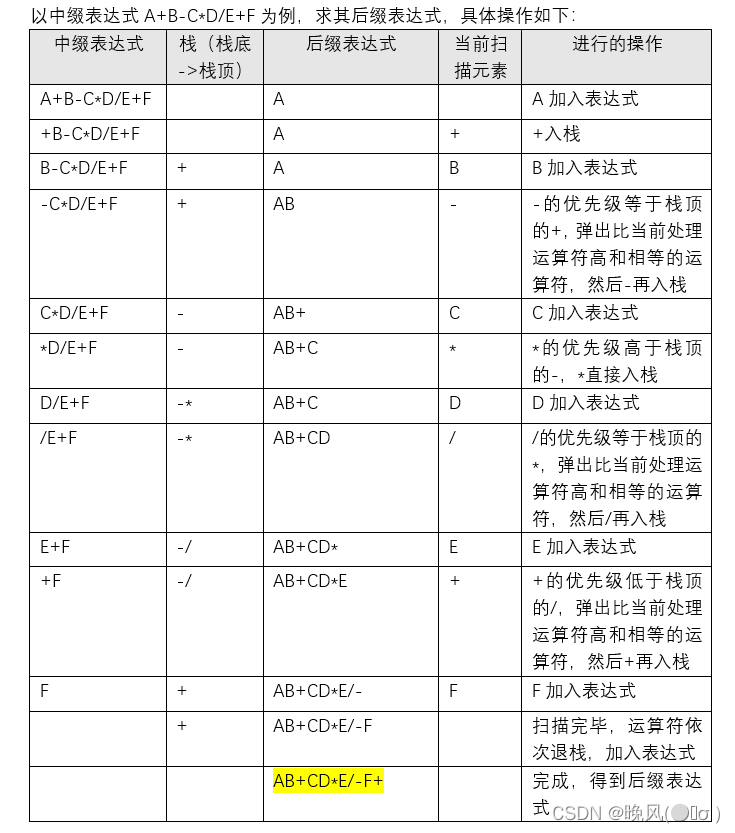
通过手工算,第一步转换为((A+B(-((C*D)/E)+F),第二步提运算符转为((AB)+(((CD)*E/)-F)+,去掉括号得到后缀表达式AB+CD*E/-F+。
例题
例1、表达式a*(b+c)-d的后缀表达式是________。
首先第一步,加上括号得:((a*(b+c))-d)
然后由于是转为后缀表达式,将符号提至对应的括号后,得:((a(bc)+)*d)-
括号去掉,即可得到后缀表达式:abc+*d-
例2、求表达式a / b + (c * d-e * f) / g的前缀表达式。
第一步也是加上括号:((a/b)+(((c*d)-(e*f))/g))
然后由于是转为前缀表达式,将符号提至对应的括号前,得:+(/(ab)/(-(*(cd)*(ef))g))
括号去掉,即可得到前缀表达式:+/ab/-*cd*efg