目录
讲义P25-将一个正整数分解质因数
示例:

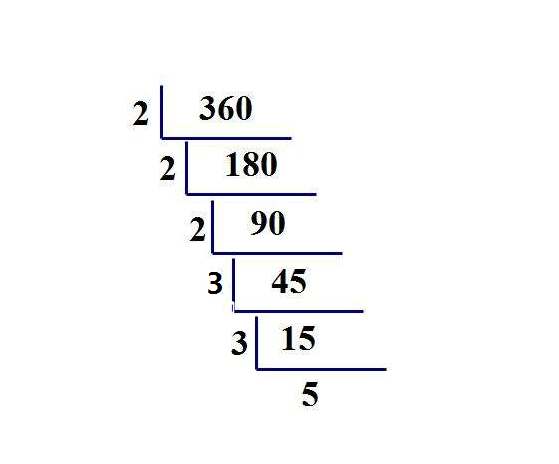
int main()
{
int i, n;
cout << "请输入一个数:";
cin >> n;
cout << n << " = ";
//为什么需要i++?比i小的数难道不能是新的n的质因子吗?
//答案是不会,因为如果比i小的数如果是n的质因子,那早就已经被分解掉了
//实际上在这个算法中,被分解的质因子是从小到大递增的
for (i = 2; i < n; i++)
{
while (n != i) //若n == i,则n的质因数就是n本身
{
//这里不需要判断i是否为质数,因为根据这个算法的特性,在遇到i之前,n中关于i的因数都已经被分解掉了,
//在遇到6之前必定已经将这个6分解为了2*33,在遇到9之前必定已经将9分解为了3*3
//因此这里的i一定是个质数
if (n % i == 0) //若i是质因数,则打印i
{
cout << i << " * ";
n = n / i;
}
else break; //若不能被i整除,则考虑i + 1
}
}
cout << n; //打印最后一个质因数,也就是当n == i时的质因数
return 0;
}?打印如下:
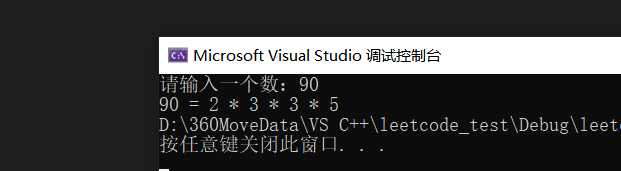
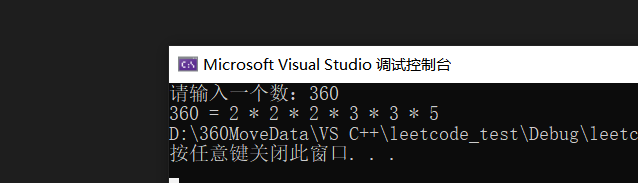
讲义P30-辗转相除法?
非递归写法:
int gcd(int a, int b)
{
? ? int r;
? ? while (b != 0)
? ? {
? ? ? ? r = a % b;
? ? ? ? a = b;
? ? ? ? b = r;
? ? }
? ? return a;
}更为简便的递归写法:
int gcd(int a, int b)
{
? ? return b == 0 ? a : gcd(b, a % b);
}讲义P32-给出年月日,计算该日是该年的第几天
按讲义上的写法来的,主要是在于数据的健壮性判断十分繁琐
/*
非整百年:能被4整除的为闰年。
整百年:能被400整除的是闰年。
*/
int is_leapyear(int year)
{
if (year % 400 == 0 || year % 4 == 0 && year % 100 != 0)
{
return 1;
}
return 0;
}
//判断该日是今年的第几天
int whichday(int year, int month, int day)
{
int mon[13] = { 0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
mon[2] = is_leapyear(year); //如果是闰年,二月份就加1天
int count = 0;
for (int i = 1; i < month; i++)
{
count += mon[i];
}
count += day;
return count;
}
int main()
{
int year, month, day;
cout << "请输入年份" << endl;
while (1)
{
cin >> year;
if (year < 0)
{
cout << "月份必须非负,请重新输入" << endl;
continue;
}
break;
}
cout << "请输入月份" << endl;
while (1)
{
cin >> month;
if (month < 1 || month > 12)
{
cout << "月份必须在1到12之间" << endl;
continue;
}
break;
}
cout << "请输入天数" << endl;
while (1)
{
cin >> day;
if (day < 1)
{
cout << "天数不能小于1" << endl;
continue;
}
if (month == 1 || month == 3 || month == 5 || month == 7 || month == 8 || month == 10 || month == 12)
{
if (day > 31)
{
cout << "您输入的天数大于" << month << "月的最大天数" << endl;
continue;
}
}
else if (month == 2)
{
if (is_leapyear(year) == 1 && day > 29) //如果是闰年的话
{
cout << "您输入的天数大于" << month << "月的最大天数" << endl;
continue;
}
else if (is_leapyear(year) == 0 && day > 28) //如果不是闰年的话
{
cout << "您输入的天数大于" << month << "月的最大天数" << endl;
continue;
}
}
else
{
if (day > 30)
{
cout << "您输入的天数大于" << month << "月的最大天数" << endl;
continue;
}
}
break;
}
printf("%d年%d月%d日是该年的第%d天", year, month, day, whichday(year, month, day));
return 0;
}讲义P56-进制转换讲解
讲义P59-打印集合M的前面100个最小数?

讲义上的代码写得不好,于是在网上搜到了这一种很有意思的写法,该写法采用了归并排序的思想:
? ? ? ? 该题的难点在于很难确定最小的n个数到底是哪n个数,现在我们假设可以将int型的y和z看成两个"数组",y记录的是 2 * a[0] + 1、?2 * a[1] + 1、?2 * a[2] + 1....,z记录的是?3 * a[0] + 1、 3 * a[1] + 1、 3 * a[2] + 1....,只要a是个递增数组,y和z也都是递增"数组",之后就可以利用归并排序的思想,每次对比y和z的大小,选取较小值入a数组,然后更新y或z的值。
int main()
{
int a[100];
a[0] = 1;
int i = 0, j = 0; //i为y"数组"的指针,j为z"数组"的指针
int y = 3, z = 4; //y"数组"的首元素为2 * a[0] + 1 = 3,z"数组"的首元素为3 * a[0] + 1 = 4
//类似归并排序
for (int k = 0; k < 100; k++)
{
if (y < z)
{
a[k] = y;
y = 2 * a[i] + 1; //y"数组"移动到下一个元素
i++;
}
else if (y == z) //由于集合的互异性,所以当出现两边的值相等时只取一个,两边的"数组"都移动
{
a[k] = y;
y = 2 * a[i] + 1;
i++;
z = 3 * a[j] + 1;
j++;
}
else
{
a[k] = z;
z = 3 * a[j] + 1; //z"数组"移动到下一个元素
j++;
}
}
for (int i = 0; i < 100; i++)
{
if (i % 10 == 0) cout << endl;
printf("%4d ", a[i]);
}
return 0;
}打印结果如下:
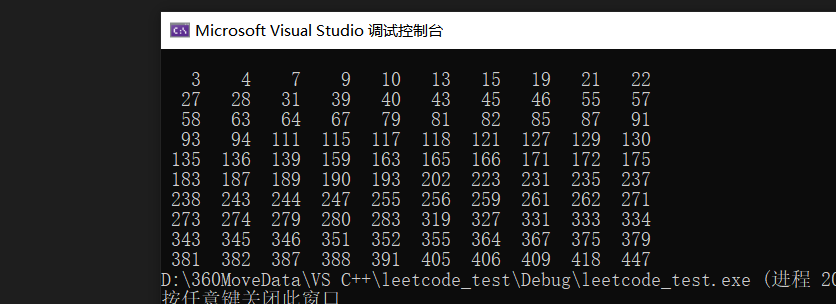
讲义P61-输入正整数n,打印集合的所有子集?
居然用到了位运算,是我掌握较为薄弱的一个方法。
对于数字0 ~ n-1而言,在一个子集每个数字有两种状态:存在和不存在,于是所有状态的组合就是所有的子集了,并且可知输入的正整数为n,子集的个数共有2 ^ n个。
根据上述,我们可以采用二进制数来代表所有的子集,1表示存在,0表示不存在。
例如输入3,则子集的总数为2^3 = 8个,集合为{0, 1, 2}。而二进制数也有8个,例如 001对应子集{2},010对应子集{1},011对应子集{1, 2}。
void powerset(int n)
{
int m = pow(2, n); //共有2^n种子集,对应2^n个二进制数
int* subset = new int[n]; //记录子集
int len; //记录每次生成的子集的长度
for (int i = 0; i < m; i++) //大循环,遍历2^个二进制数,确定2^n种子集
{
len = 0;
for (int j = 0; j < n; j++) //遍历数字0 ~ n-1,检查每个数字是否存在于当前子集中
{
int tmp = 1 << j; //将1左移j位,用tmp来检查第j个数字是否存在于当前子集中
if (i & tmp)
{
subset[len++] = j; //若存在则记录
}
}
cout << "{";
for (int j = 0; j < len; j++)
{
cout << subset[j];
if (j < len - 1) cout << ", ";
}
cout << "}" << endl;
}
}
int main()
{
int n;
cin >> n;
powerset(n);
return 0;
}输出如下:
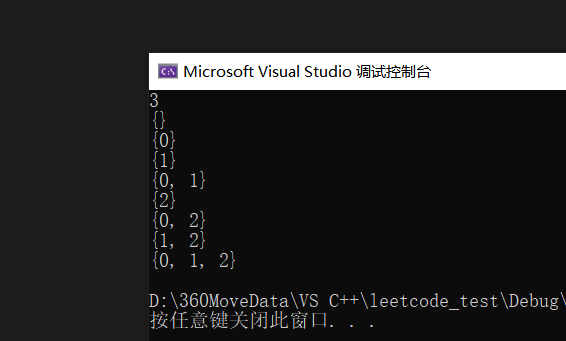
讲义P67-求所有元素个数为M的子集?
这道题用讲义上的位运算写法有点麻烦,可以直接用dfs来写。这里我直接让原集合中的元素都是1 ~ N - 1了。
int subset[100];
//N是集合中的元素个数,M表示要求元素个数为M的子集
//cur数组用于保存当前子集中的元素,len为cur数组中当前的元素个数
//index表示当前循环需要从下标为index的元素开始遍历
//每调用一次dfs函数,会确定当前子集中len位置的元素
void dfs(int cur[], int len, int M, int index, int N)
{
//如果当前子集中的元素个数为M,打印
if (len == M)
{
cout << "{";
for (int i = 0; i < M; i++)
{
cout << cur[i];
if (i < len - 1) cout << ", ";
}
cout << "}" << endl;
return;
}
for (int i = index; i < N; i++)
{
cur[len] = subset[i];
dfs(cur, len + 1, M, i + 1, N);
}
}
int main()
{
int N, M;
cin >> N >> M;
for (int i = 0; i < N; i++)
{
subset[i] = i + 1;
}
int cur[100];
dfs(cur, 0, M, 0, N);
return 0;
}输出如下:
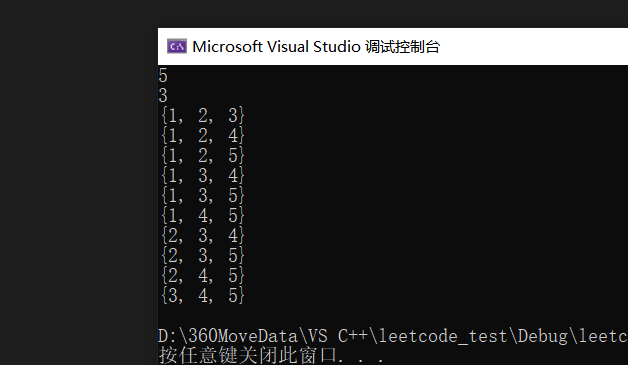
关于dfs函数中的遍历我原先写的是这样:
for (int i = index; i < N; i++)
{
//选取
cur[len] = subset[i];
dfs(cur, len + 1, M, i + 1, N);
//不选取
dfs(cur, len, M, i + 1, N);
}对于cur[i],分为选取和不选取两种情况,但是这样会导致相同的子集重复打印,例如集合{1,2,3},如果按照上面这种写法,会重复打印子集{2,3}两次。
而下面这种正确的这种写法,其作用可以理解为每次调用dfs函数时,确定子集中len位置的元素,即每次确定cur[len]的值,这样一来可以保证在位置0~M - 1上,每个位置的元素不会重复出现
for (int i = index; i < N; i++)
{
cur[len] = subset[i];
dfs(cur, len + 1, M, i + 1, N);
}讲义P68-实现任意两个不同进制非负整数之间的转换
实现输入多组数据
这道题要求能够输入多组测试数据,先了解一下c++中如何输入多组数据:
int a;
string s;
while (cin >> a >> s)
{
cout << a << " " << s << endl;
}利用while循环和cin即可,只要输入的a是int型、s是string型,就能够不断循环、不断输入下去。但是如果输入的a不是int型,或者输入的s不是string型,while循环就会中断。
本题代码
回到该题,实现代码如下:
int main()
{
int a, b;
string n;
//多组的测试数据,将a进制的整数n转换为b进制
while (cin >> a >> n >> b)
{
cout << a << "进制:" << n << endl;
int ten = 0; //存储10进制数
//先将a进制转换为10进制
for (int i = 0; i <= n.size() - 1; i++)
{
int x = 0; //记录该位数字
if ('0' <= n[i] && n[i] <= '9')
{
x = n[i] - '0';
}
else if ('a' <= n[i] && n[i] <= 'z')
{
x = n[i] - 'a' + 10;
}
else if ('A' <= n[i] && n[i] <= 'Z')
{
x = n[i] - 'A' + 10;
}
ten = ten * a + x; //这个地方就类似于10进制中的ten * 10 + x
}
cout << "10进制:" << ten << endl;
//再将10进制转换为b进制
string ans;
while (ten > 0)
{
char ch;
int x = ten % b; //记录该位数字
ch = x < 10 ? x + '0' : x - 10 + 'A';
ans = ch + ans;
ten /= b;
}
cout << b << "进制:" << ans << endl;
}
return 0;
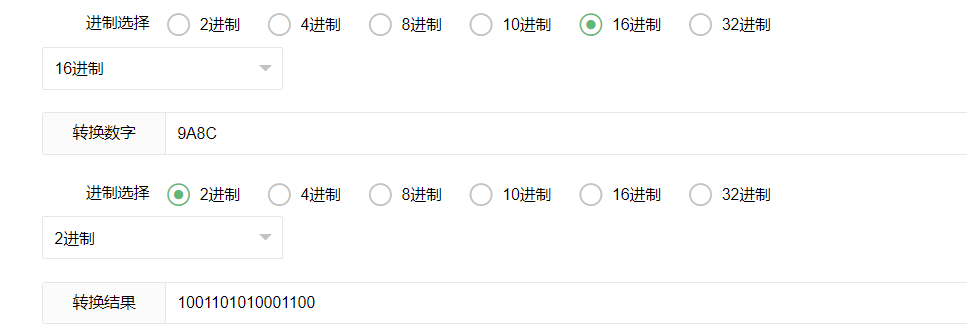
}结果如下:
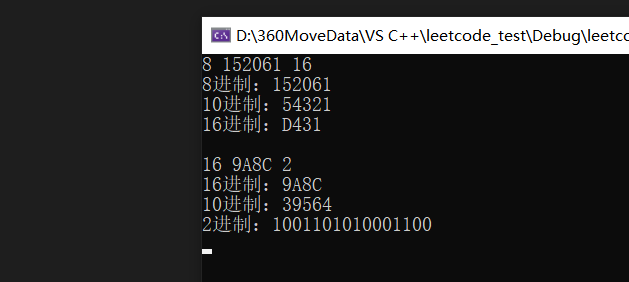
与网站上所给的结果相同:
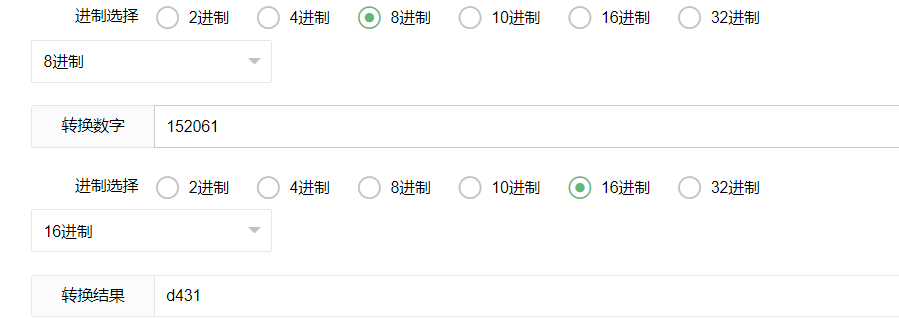
讲义P80-交换两个向量的位置?
讲义P88-两个机器人的对话
不知道是不是原题就这样,这里描述了一下对话规则之后要没讲这题到底要我写什么。。
看了给的代码,才明白了这题是要对任意给出的一个字符串,判断是不是符合规则的对话内容
int main()
{
string talk;
cout << "请输入字符串:";
cin >> talk;
int n = talk.size();
int i = 0;
//while循环即为对话过程
while(i < n)
{
//先由M1开始说话
//当机器人说的不是数字时,必须继续说话
while (i < n && (talk[i] == 'Y' || talk[i] == 'N')) i++;
//当机器人说出数字时,自己必须停止说话,此时对方可以选择接着说话或停止对话
if (i < n && talk[i] == '2') i++;
//这里有两种情况:1、说的既不是2也不是Y或N 2、还没说出数字时对话就已经结束了
else break;
//接着由M2说话
//当机器人说的不是数字时,必须继续说话
while (i < n && (talk[i] == 'y' || talk[i] == 'n')) i++;
//当机器人说出数字时,自己必须停止说话,此时对方可以选择接着说话或停止对话
if (i < n && talk[i] == '1') i++;
//这里有两种情况:1、说的既不是1也不是y或n 2、还没说出数字时对话就已经结束了
else break;
}
if (talk[i - 1] == '1' || talk[i - 1] == '2')
{
if (i == n) cout << "该字符串是两个机器人的对话" << endl;
}
else cout << "该字符串不是两个机器人的对话" << endl;
return 0;
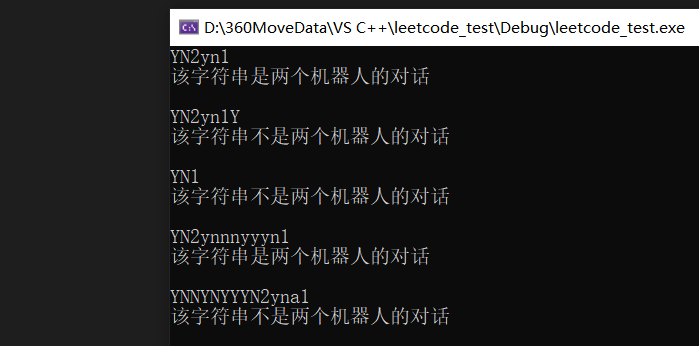
}结果如下:?
讲义P91-对n个字符串按字典序排序
字符数组的相关操作
这题居然限定了只能用字符数组,字符数组一直是我大一时较为薄弱的点,重新熟悉一下用法
//字符数组的初始化,两种方式等价
char str1[20] = { 'a', 'b', 'c', 'd', '\0' }; //注意其中每个字符是char类型的,最后需要手动添加'\0'
char str2[20] = "abcd"; //可以自动添加'\0'
char str3[20];
//可以直接用cin和cout输入和输出
scanf("%s", str3); //也可以cin >> str3
printf("%s", str3); //也可以cout << str3
//字符串的赋值运算
strcpy(str1, str2); //将str2复制到str1中
//字符串的比较运算
strcmp(str1, str2); //比较字典序,如果str1大于str2就返回正数,等于就返回0,小于就返回负数
//字符串的拼接操作
strcat(str1, str2); //将str2拼接到str1后面 //单词concat:合并多个字符串
//求字符串的长度
int len = strlen(str1);本题代码
void Sort(char st[][10], int n)
{
char tmp[10];
//简单选择排序
for (int i = 0; i < n; i++)
{
int mini = i;
for (int j = i + 1; j < n; j++)
{
if (strcmp(st[j], st[mini]) < 0)
{
mini = j;
}
}
if (mini != i)
{
strcpy_s(tmp, st[i]);
strcpy_s(st[i], st[mini]);
strcpy_s(st[mini], tmp);
}
}
}
int main()
{
char st[5][10] = { "bcd", "f", "abc", "adc", "bcde" };
Sort(st, 5);
for (int i = 0; i < 5; i++)
{
printf("%s ", st[i]);
}
return 0;
}输出如下:

讲义P92-将0元素移动到数组后面,非0元素保持有序
讲义P93-删除数组中值在x到y之间的所有元素
见过几次的题型,还是忘记了移动的操作了
//删除值在x到y之间的所有元素
int del(int A[], int n, int x, int y)
{
int k = 0; //记录当前被删除的元素的个数
for (int i = 0; i < n; i++)
{
if (x <= A[i] && A[i] <= y)
{
k++;
}
else
{
A[i - k] = A[i]; //遇到非删除元素,就将其往前移动k个位置
}
}
return n - k; //返回删除后的元素个数
}
int main()
{
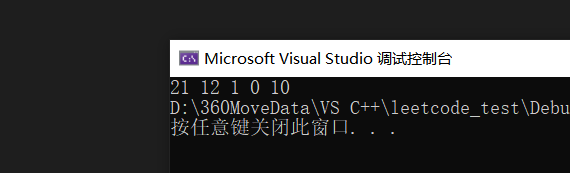
int A[10] = { 21, 7, 6, 12, 1, 0, 5, 3, 4, 10 };
int n = del(A, 10, 3, 7); //删除3到7之间的所有元素
for (int i = 0; i < n; i++)
{
cout << A[i] << " ";
}
return 0;
}结果如下:
????????
讲义P95-删除数组中值相同的元素
以往遇到这种问题直接用map,但是考研应该不能用这玩意吧,这题其实与上题大致相同,虽然我还是不会。
主要是第二层循环时要将所有与a[i]不相同的元素都向前移动,我原先想的是第二层循环碰到第一个与a[i]不相同的元素就移动然后直接退出循环了,但是这种想法是错的,例如{ 1, 2, 3, 3, 3, 4, 4, 5?},若采用我原先的思路将3去重后变为{ 1, 2, 3, 4, 3, 4, 4,?5?},那问题来了,第一层循环下一次的i指针应该指向哪里呢?这三个无论指向哪个都不行:{ 1, 2, 3, 4, 3, 4, 4,?5?}
//值相同的元素只保留一个,其他删除
int del(int a[], int n)
{
int k; //记录当前被删除的元素的个数
//两层循环,第一层循环遍历数组中剩余的元素,第二层循环进行去重,并把其他元素向前移动
for (int i = 0; i < n; i++)
{
int tmp = a[i];
k = 0; //每次要删除一个新的元素时都要重置一下删除的个数
for (int j = i + 1; j < n; j++)
{
if (a[j] == tmp)
{
k++;
}
else a[j - k] = a[j]; //与a[i]不相同的元素往前移动k个位置
}
n -= k; //删除了k个元素,其他的元素都往前移动了k个位置,因此后面的几个位置上的元素没有意义,不用遍历
}
return n; //返回删除后的元素个数
}
int main()
{
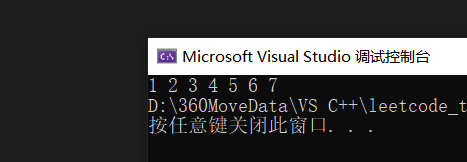
int a[10] = { 1, 2, 3, 3, 3, 4, 5, 5, 6, 7 };
int n = del(a, 10);
for (int i = 0; i < n; i++)
{
cout << a[i] << " ";
}
return 0;
}结果如下:
????????????????
讲义P101-用数组精确计算M/N的各小数位的值
但凡与浮点数、小数位涉及上的问题,在我看来都是恶心。。
这题被输出结果整麻了,不过如果是手写代码的话就不用那么在意结果的严谨性了
int main()
{
int M, N ; //M为第一位被除数,N是除数
cout << "请输入被除数:";
cin >> M;
cout << "请输入除数:";
cin >> N;
if (N > M) //如果分子大于分母,先算出整数部分
{
cout << "整数部分:" << endl;
cout << M / N << endl;
M = M % N;
}
int a[100] = { 0 }; //存放商,即各位小数
int b[100] = { 0 }; //存放余数
int k = 0; //小数个数
int begin = 0, end = 0; //记录循环节的起止位置
while (M != 0) //当余数不为0时,说明除法运算还未结束,需要继续循环
{
a[k] = M * 10 / N; //此次除法运算的商
b[k] = M * 10 % N; //此次除法运算的余数
M = M * 10 % N; //更新,M是此次除法运算的余数,也将作为下次除法运算的被除数
//遍历余数数组,当余数出现重复时说明已经出现并完成了一次循环节
for (int j = 0; j < k; j++)
{
if (b[j] == M)
{
begin = j + 1; //循环节第一次出现的位置是第j + 1位,a[j]
end = k; //循环节结束的位置是第 k 位,a[k - 1]
M = 0; //设置跳出循环条件
break;
}
}
k++;
}
for (int i = 0; i < k; i++)
{
cout << a[i] << " ";
}cout << endl;
cout << "begin: " << begin << endl;
cout << "end: " << end << endl;
return 0;
}示例:
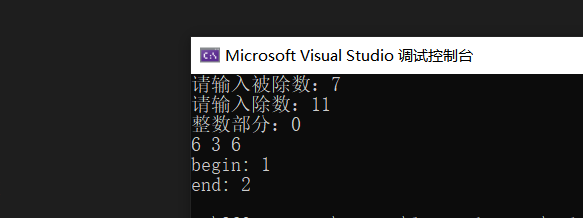
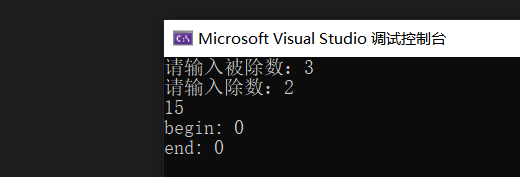
讲义P105 生成螺旋矩阵
不太喜欢书上给的代码,通过找规律来做题有时候会给思考增加很大的负担,不如直接模拟螺旋矩阵的生成过程。
我采用了方向数组来控制在二维数组中的移动方向,因为赋值的方向就是右→下→左→上依次循环,每次沿着同个方向一直移动,直到坐标超出10*10或者碰到已经赋值过的位置,就改变方向
#define n 10
//方向数组
int dir[4][2] =
{
{0, 1}, //右
{1, 0}, //下
{0, -1}, //左
{-1, 0} //上
};
int main()
{
int num = 1;
int a[10][10] = {0};
int k = 0; //方向数组的指针
int i = 0, j = 0; //起始坐标
while (num <= n * n) //从 1 打印到 n * n
{
a[i][j] = num;
num++;
int nexti = i + dir[k][0];
int nextj = j + dir[k][1];
//如果下一个坐标超出范围,或者下一个位置已经有数字了,就改变方向
if (nexti >= 10 || nextj >= 10 || a[nexti][nextj] != 0)
{
k = (k + 1) % 4;
}
i = i + dir[k][0];
j = j + dir[k][1];
}
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < 10; j++)
{
printf("%4d", a[i][j]);
}cout << endl << endl;
}
return 0;
}以10*10矩阵为例:
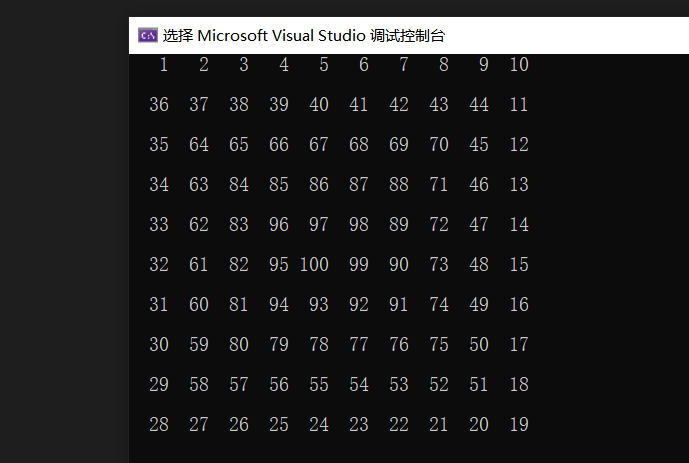
讲义P106 二维数组排序
冒泡排序版
本来是想仿照外排序的那个归并排序的方法来写的,但是想了想实在有点麻烦,于是还是使用书上用指针来写冒泡的方法,确实十分简便。
#define n 5
void bubble_sort(int a[][n])
{
//不能写int* p = a,因为a是int(*)[5]类型,只有当a为一维数组时可以这么写
int* p = &a[0][0];
for (int i = n * n - 1; i >= 0; i--)
{
bool flag = false;
for (int j = 0; j < i; j++)
{
if (*(p + j) > *(p + j + 1))
{
int temp = *(p + j);
*(p + j) = *(p + j + 1);
*(p + j + 1) = temp;
flag = true;
}
}
if (!flag) break;
}
}
int main()
{
int a[n][n] =
{
{14, 9, 42, 9, 19},
{39, 8, 2, 91, 43},
{47, 84, 77, 12, 0},
{23, 29, 7, 3, 5},
{64, 32, 15, 18, 82}
};
bubble_sort(a);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cout << a[i][j] << " ";
}cout << endl;
}
return 0;
}?结果:
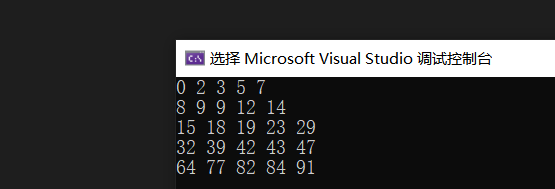 ?
?
插入排序版?
同样具有稳定性的插入排序也可以用此法写:
#define n 5
void insert_sort(int a[][n])
{
//不能写int* p = a,因为a是int(*)[5]类型,只有当a为一维数组时可以这么写
int* p = &a[0][0];
for (int i = 0; i < n * n; i++)
{
int tmp = *(p + i);
int j;
for (j = i - 1; j >= 0 && *(p + j) > tmp; j--)
{
*(p + j + 1) = *(p + j);
}
*(p + j + 1) = tmp;
}
}
int main()
{
int a[n][n] =
{
{14, 9, 42, 9, 19},
{39, 8, 2, 91, 43},
{47, 84, 77, 12, 0},
{23, 29, 7, 3, 5},
{64, 32, 15, 18, 82}
};
insert_sort(a);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cout << a[i][j] << " ";
}cout << endl;
}
return 0;
}结果:
 ?
?
归并排序版
归并排序具有稳定性,也符合要求,虽然用归并排序写挺麻烦的,但用来练习练习
#define n 5
int b[n * n];
void merge(int a[][n], int low, int mid, int high)
{
int i, j, k;
int* p = &a[0][0];
for (int k = low; k <= high; k++)
{
b[k] = *(p + k);
}
for (i = low, j = mid + 1, k = low; i <= mid && j <= high; k++)
{
//是通过在b数组中比较,再把b数组中的数字转移到a数组中,不要搞混了
if (b[i] <= b[j])
{
*(p + k) = b[i++];
}
else
{
*(p + k) = b[j++];
}
}
while (i <= mid)
{
*(p + k) = b[i++];
k++;
}
while (j <= high)
{
*(p + k) = b[j++];
k++;
}
}
void merge_sort(int a[][n], int low, int high)
{
if (low < high)
{
int mid = (low + high) / 2;
merge_sort(a, low, mid);
merge_sort(a, mid + 1, high);
merge(a, low, mid, high);
}
}
int main()
{
int a[n][n] =
{
{14, 9, 42, 9, 19},
{39, 8, 2, 91, 43},
{47, 84, 77, 12, 0},
{23, 29, 7, 3, 5},
{64, 32, 15, 18, 82}
};
merge_sort(a, 0, n * n - 1);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cout << a[i][j] << " ";
}cout << endl;
}
return 0;
}结果:
?