记忆化搜索概述

记忆化搜索是一种搜索的形式，对搜索的结果用数组或其他数据结构记录下来。若当前状态搜索过了，则返回已存储的答案。这样，每个状态最多计算1次。
我们以斐波那契数列为例，用递归实现的fib数组计算代码是这样的：

int fib(int xn){
	if(n==1||n==2){
		return 1;
	}
	return fib(n-1)+fib(n-2);
}

搜索树是长这样的
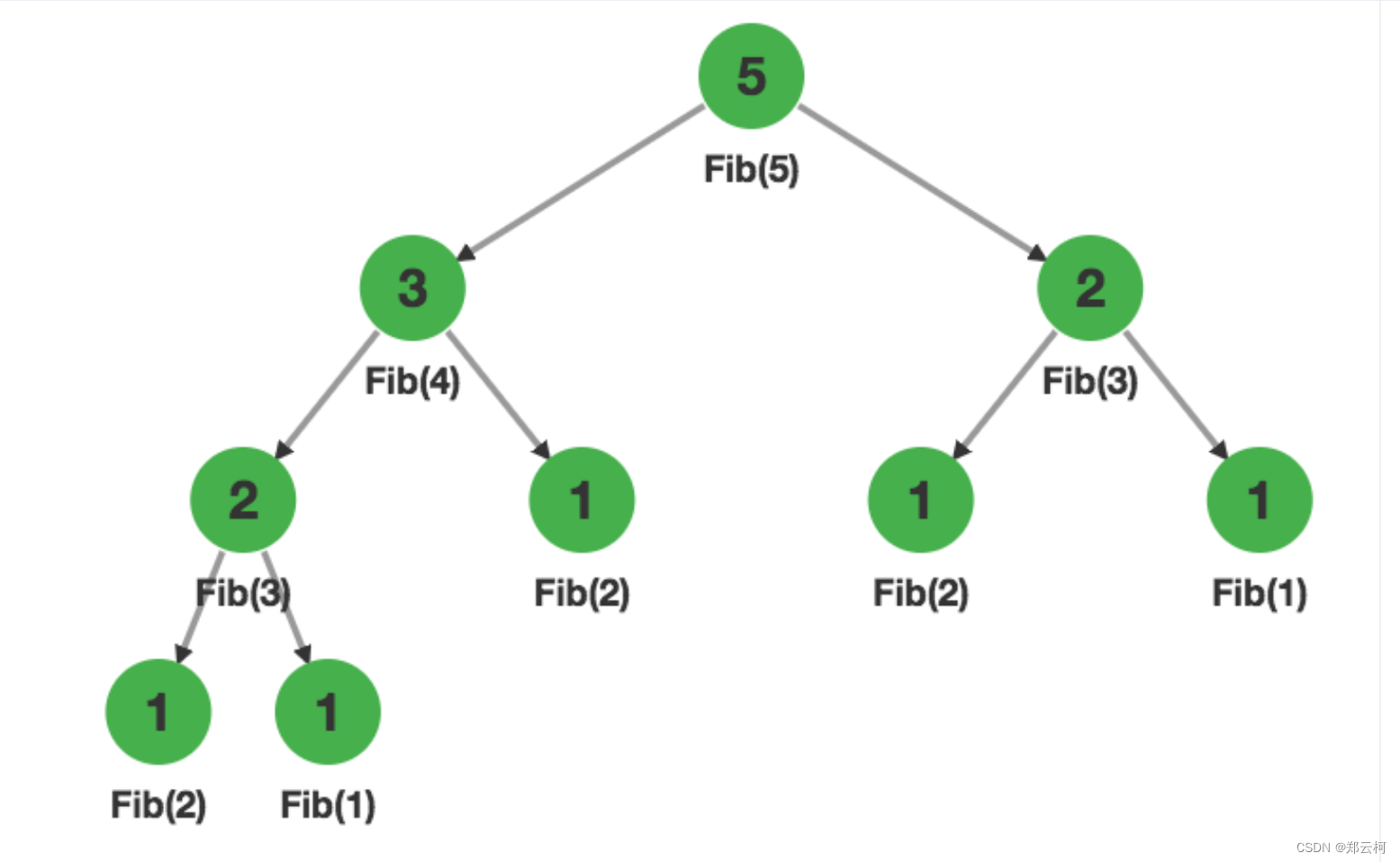
在这里插入图片描述
我们可以发现，为了求 $F i b (5)$ ，会先求 $F i b (4)$ ，然后求出 $F i b (3)$ .在求 $F i b (4)$ 的时候，实际上已经把 $F i b (3)$ 求出来了，而求 $F i b (5)$ ，又计算了一次，这些计算是多余的，因为不管在任何情况下计算出的 $F i b (3)$ ，结果都一模一样。
所以，我们求出 $F i b (x)$ 后，用一个数组 $F [x]$ 来记录这个数，如果以后需要 $F i b (x)$ 的值，直接从数组中取出就可以了。

代码示例：

#include <iostream>
using namespace std;
const int mod = 1000000009;
int f[10000];
int fib(int x) {
    if(f[x]){
        return f[x];
    }
    if (x <= 2) {
        return f[x]=1;
    }
    else {
        return f[x]=(fib(x - 1) + fib(x - 2))%mod;
    }
}

int main() {
    int n;
    cin >> n;
    cout << fib(n) << endl;
    return 0;
}

记忆化搜索与动态规划

相比较于记忆化搜索，动态规划一般要遍历所有的状态，神之包括一些不可行的状态，而记忆化搜索可以进行剪枝包括可行性剪枝、最优性剪枝等，避免了一些多余的计算。
记忆化搜索的程序思路好想但容易写错，通常代码要短一些
对比如下：

	记忆化搜索	动态规划
代码量	<
时间复杂度	=
运行效率	≥
思维速度	≤
实现难度	≥
计算难度	自顶向下	自底向上
解决范围	>
通常，一道动态规划算法能解决的问题，也可以用记忆化搜索的方式解决；但能有记忆化搜索解决的问题却不一定能用动态规划的多重循环方式解决。
记忆化搜索的本质就是将深度优先搜索的过程，通过避免重复计算同一个状态的结果，从而将时间复杂度优化到多项式复杂度。

递归函数

我们要实现一个程序，计算函数 $w (a, b, c)$ 的值
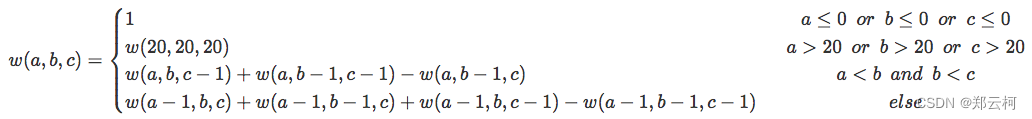
请添加图片描述
我们很容易就可以想到一个递归实现的方法，

#include <iostream>
using namespace std;
int w(int a, int b, int c) {
    if (a <= 0 || b <= 0 || c <= 0) {
        return 1;
    } else if (a > 20 || b > 20 || c > 20) {
        return w(20, 20, 20);
    } else if (a < b && b < c) {
        return w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);
    } else {
        return w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1)- w(a - 1, b - 1, c - 1);
    }
}
int main() {
    int a, b, c;
    cin >> a >> b >> c;
    cout << w(a, b, c) << endl;
    return 0;
}

但可以发现输入19 19 19后要跑很久才能出结果，原因其实和前面的斐波那契额数列原因一样，同一种情况算了不止一次，我们可以将其过程加上记忆化
用 $f [a] [b] [c]$ 记录 $w (a, b, c)$ 的值
用 $g o t [a] [b] [c]$ 记录 $w (a, b, c)$ 是否计算过

#include <iostream>
using namespace std;
int f[100][100][100];
bool got[100][100][100];
int w(int a, int b, int c) {
    if(got[a][b][c]){
        return f[a][b][c];
    }
    got[a][b][c]=true;
    if (a <= 0 || b <= 0 || c <= 0) {
        return f[a][b][c]=1;
    } else if (a > 20 || b > 20 || c > 20) {
        return f[a][b][c]=w(20, 20, 20);
    } else if (a < b && b < c) {
        return f[a][b][c]=w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);
    } else {
        return f[a][b][c]=w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1)- w(a - 1, b - 1, c - 1);
    }
}
int main() {
    int a, b, c;
    cin >> a >> b >> c;
    cout << w(a, b, c) << endl;
    return 0;
}

这样，就可以将时间复杂度降到 $O (a b c)$

滑雪问题

蒜头君喜欢滑雪这并不奇怪，因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。蒜头君想知道一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子

 1  2  3  4  5

16 17 18 19  6

15 24 25 20  7

14 23 22 21  8

13 12 11 10  9

一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-…-3-2-1更长。事实上，这是最长的一条。

可以很容易地写出一个不带记忆化的dfs

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 105;
int h[N][N];  // 每个点的高度
int dx[4] = {0, -1, 0, 1};  // 方向数组 x 轴
int dy[4] = {1, 0, -1, 0};  // 方向数组 y 轴
int n, m, ans;
int dfs(int x, int y) {
    if (x < 0 || x >= n || y < 0 || y >= m) {
        return 0;
    }
    int mx = 0;
    for (int i = 0; i < 4; i++) {
        if (h[x + dx[i]][y + dy[i]] < h[x][y]) {
            mx = max(mx, dfs(x + dx[i], y + dy[i]));
        }
    }
    return mx + 1;
}
int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> h[i][j];
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            ans = max(ans, dfs(i, j));
        }
    }
    cout << ans << endl;
    return 0;
}

加上记忆化也就是 $d p [x] [y]$ 代表在下 $x, y$ 这个位置能滑过的最大值

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 105;
int h[N][N];  // 每个点的高度
int dx[4] = {0, -1, 0, 1};  // 方向数组 x 轴
int dy[4] = {1, 0, -1, 0};  // 方向数组 y 轴
int n, m, ans;
int dp[N][N];
int dfs(int x, int y) {
    if (x < 0 || x >= n || y < 0 || y >= m) {
        return 0;
    }
    if(dp[x][y]){
        return dp[x][y];
    }
    int mx = 0;
    for (int i = 0; i < 4; i++) {
        if (h[x + dx[i]][y + dy[i]] < h[x][y]) {
            mx = max(mx, dfs(x + dx[i], y + dy[i]));
        }
    }
    return dp[x][y]=mx + 1;
}
int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> h[i][j];
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            ans = max(ans, dfs(i, j));
        }
    }
    cout << ans << endl;
    return 0;
}