PS：本篇文章参考了大佬 “wmy0217_” 所整理的博客
https://blog.csdn.net/wmy0217_/article/details/105438163?ops_request_misc=&request_id=&biz_id=102&utm_term=%E6%9C%80%E7%9F%AD%E8%B7%AF&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-105438163.nonecase&spm=1018.2226.3001.4187首先我们可以用一张图来说明最短路算法的总体框架：?
?
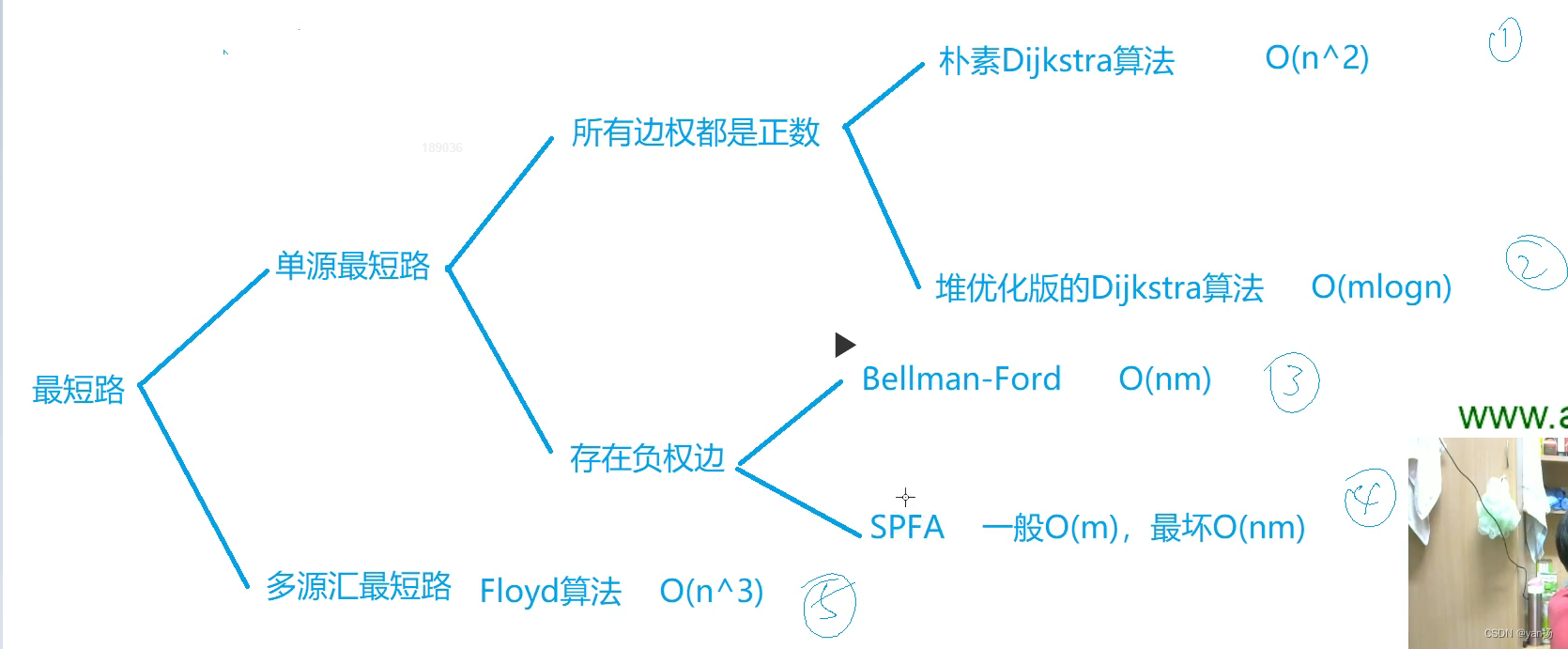
?首先解释图中的几个概念：
单源最短路：就是固定起点，然后到不同终点的最短路径
多远汇最短路：起点和终点都不固定，随机给两个点都可以求出最短路
时间复杂度中的 n：n 的含义是图中结点的数量
时间复杂度中的m：边的数量
接下来拓展一下稠密图和稀疏图的概念：
稠密图：一个结点最多可以有 n - 1 条边来和其他的结点相连 所以总的边数就是 n ^2 级别
稀疏图：一般来说一个节点只有一条边，总的边数是 n 级别
目录
一、朴素版本的 Dijkstra
适用场景关键词：正权边，稠密图，固定起点
引用大佬一张好图：
核心思路：
步骤1 是为了固定我们的起点（dist[1] = 0） 然后把其他的点的距离初始化为无穷大（后边我们会对能到达的点一步一步更新为最短路的）
步骤2 是进行 n 次循环，每次在循环中寻找还没有确定最短路的点且距离起点最近的点，找到这个点以后用这个点去更新其他的点
核心代码：
for(int i=0; i<n; i++)
{
int t = -1;
for(int j=1; j<=n; j++) // 在没有确定最短路中的所有点找出距离最短的那个点 t
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t=j;
st[t]=true; // 代表 t 这个点已经确定最短路了
for(int j=1; j<=n; j++) // 用 t 更新其他点的最短距离
dist[j] = min(dist[j],dist[t]+g[t][j]);
}
为什么是 n 次循环？??
因为我们每一次循环其实是确定一个点的最短距离，经过 n 次就可以找到所有点的最短距离啦
为什么 Dijkstra 不能用于负权边？
后边在讲完 堆优化版本后?会解释
定义一个 st 数组的意义？
st 数组其实就是图中所说的集合，方便我们确定那些点已经确定了 最短路了，我们要寻找那些还没确定最短路的距离起点最近的点
先来一道题练练手：
例题：
给定一个n个点m条边的有向图，图中可能存在重边和自环，所有边权均为正值。请你求出1号点到n号点的最短距离，如果无法从1号点走到n号点，则输出-1。
输入格式
第一行包含整数n和m。接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。
输出格式
输出一个整数，表示1号点到n号点的最短距离。如果路径不存在，则输出-1。
数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。输入样例：
3 3
1 2 2
2 3 1
1 3 4输出样例：
3
代码实现：
import java.util.*;
public class Main{
static int N = 510,M = 10010;
static int n,m;
static int max = 0x3f3f3f3f;
static int[][] g = new int[N][N];
static int[] d = new int[N];
static boolean[] st = new boolean[N];
public static void dijkstra() {
Arrays.fill(d,max); //我们一开始默认所有的点距离起点都是无穷大，后边一步一步确定最短路
d[1] = 0; //固定起点
for (int i = 0; i < n; i ++) { //外边这层循环纯粹为了循环n次 确定n个点的最短路
int t = -1; //t 初始化为谁都无所谓，只要知道t是用来找到没在集合中的距离起点最近的结点就行
for (int j = 1; j <= n; j ++) {
if (!st[j] && (t == -1 || d[j] < d[t])) {
t = j;
}
}
st[t] = true; //这个点要进集合了（它的最短路已经确定了）
for (int j = 1; j <= n; j ++) { // 用这个点去更新所有的点
d[j] = Math.min(d[j],d[t] + g[t][j]);
}
}
if (d[n] == max) System.out.print(-1);
else System.out.print(d[n]);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
for (int i = 1; i <= n; i ++) { //一开始初始化所有的点的权值都为“互相之间不可到达”即无穷大
Arrays.fill(g[i],max);
}
for (int i = 0; i < m; i ++) {
int x = sc.nextInt();
int y = sc.nextInt();
int z = sc.nextInt();
g[x][y] = Math.min(g[x][y],z); // 由于可能出现重边，所以一定要选择最小的权值
}
dijkstra();
}
}几个小 tips:
1、储存权值时，是有可能出现重边的，所以记得更新权值为最小的
2、由于使用的是邻接矩阵存储，所以我们后边更新任意两个点的距离其实有可能不能到达的，因此任意两个点的距离初始化为无穷大
二、堆优化版 Dijkstra
我们已经了解了普通版本的 Dijkstra ，我们发现每次都要在还没确定最短路的点中寻找距离起点最近的点，这让我们自然而然想到一种数据结构（优先队列），我们知道优先队列寻找最小值的时间复杂度是 log n 级别的，因此我们对其进行优化
适用场景关键词：正权边，起点固定，稀疏图
1、稀疏图如何存储？
其实本质上是静态链表，采用 h 数组存储边的起点，它的拉链上就存储它的边的终点，w 数组用来存储权值（当然，下标都是idx，目的是唯一映射便于区分），idx 从0 开始，作为 ne，e,的下标
2、优先队列里究竟要存什么？怎么存?
优先队列我们可以使用 PriorityQueue ，我们使用优先队列是为了获取未确定最短路的最近距离的点，因此我们需要知道队列里存的是那个结点，距离是多少，因此我们需要定义一种结构体（属性包含结点的编号和距离），而且由于要存储在优先队列中，因此要实现 compareTo（）方法。
3、采用邻接表的话，重边如何处理？
由于我们每次选取最近的结点都是在优先队列中选的，我们还是使用 st 数组，如果当前结点已经确定最短路了（st 为 true）我们就跳过当前点
4、为什么堆优化版 Dijkstra 不需要对权值数组初始化为无穷大？
其实本质上是由于我们采取了邻接表存储边，因此我们保证了扩展每条边时一定是可达的！所以不需要初始化（我们初始化就是为了防止不可达的边对我们更新距离造成干扰）
5、堆优化版 Dijkstra 时间复杂度如何分析？
??每次找到最小距离的点沿着边更新其他的点，若dist[j] > distance + w[i]，表示可以更新dist[j]，更新后再把j点和对应的距离放入小根堆中。由于点的个数是n，边的个数是m，在极限情况下（稠密图m=n(n?1)2m=n(n?1)2）最多可以更新m回，每一回最多可以更新nn个点（严格上是n - 1个点），有m回，因此最多可以把n2个点放入到小根堆中，因此每一次更新小根堆排序的情况是O(log(n2))，一共最多m次更新，因此总的时间复杂度上限是O(mlog((n2)))=O(2mlogn)=O(mlogn）
代码实现：
import java.util.*;
public class Main{
static int N = 150010, M = 150010;
static int idx,m,n;
static int max = 0x3f3f3f3f;
static int[] h = new int[N],e = new int[M],ne = new int[M],d = new int[N],w = new int[M];
static boolean[] st = new boolean[N];
public static void add(int a,int b,int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
public static void dijkstra() {
Arrays.fill(d,max);
d[1] = 0;
PriorityQueue<PII> q = new PriorityQueue<>();
q.add(new PII(1,0));
while (!q.isEmpty()) {
PII t = q.poll();
int x = t.x;
int y = t.y;
if (st[x]) continue;
st[x] = true;
for (int i = h[x]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] > y + w[i]) {
d[j] = y + w[i];
q.add(new PII(j,d[j]));
}
}
}
if (d[n] == max) System.out.print(-1);
else System.out.print(d[n]);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
Arrays.fill(h,-1);
for (int i = 0; i < m; i ++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
add(a,b,c);
}
dijkstra();
}
static class PII implements Comparable<PII> {
int x;
int y;
public PII (int x,int y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(PII o) {
return Integer.compare(y,o.y);
}
}
}为什么 Dijkstra 不能用于有负权的最短路问题？
三、Bellman-Ford 算法
bellman-ford 算法是通过 n 次循环，每次循环都能确定边数为当前次数的点的最短路（通过松弛操作实现），因为一共最多有n 条边的最短路，因此我们一定能找到所有点的最短路
偷大佬一张好图：
1、spfa 算法最差时间复杂度和 bellman -ford 是相同的，我为什么还需要bellman-ford？
首先类比 spfa 算法的时间复杂度发现似乎 bellman-Ford 算法似乎没有优势?，但有些情况下是不能用 spfa 的（有边数限制的情况），因为我们 bellman-ford 是通过松弛操作的，因此我们最外层的循环其实是为了维持边数的限制。
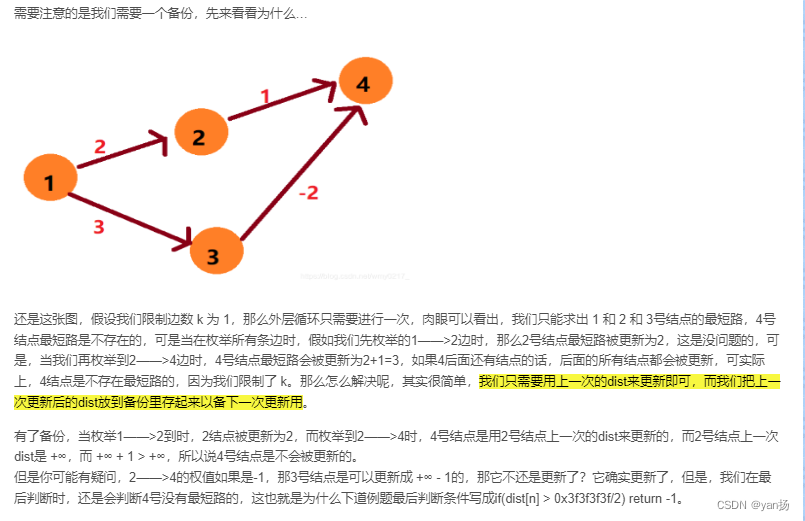
2、有边数限制进而带来的情况（串联）
串联就是我们要求边数的情况下，进而导致有些点虽然可以到达，但他的边数超出了限制。因此我们还是要判定它为“不可达”，此时如果没有备份数组，那我们所有的点都会被判定为“可达”（即使它的边数超过了限制），所以此时需要一个备份数组，来存储我们上一次更新的结果
这里可以参考大佬的实例解析：
?例题加代码实现：
给定一个?n?个点?m?条边的有向图，图中可能存在重边和自环，?边权可能为负数。
请你求出从?1?号点到?n?号点的最多经过?k?条边的最短距离，如果无法从?1?号点走到?n?号点，输出?
impossible。注意：图中可能?存在负权回路?。
输入格式
第一行包含三个整数?n,m,k,。
接下来?m?行，每行包含三个整数?x,y,z,，表示存在一条从点?x到点?y?的有向边，边长为?z。
输出格式
输出一个整数，表示从?11?号点到?nn?号点的最多经过?kk?条边的最短距离。
如果不存在满足条件的路径，则输出?
impossible。数据范围
1≤n,k≤5001≤n,k≤500,
1≤m≤100001≤m≤10000,
任意边长的绝对值不超过?1000010000。输入样例：
3 3 1 1 2 1 2 3 1 1 3 3输出样例：
3
import java.util.*;
public class Main{
static int N = 510,M = 10010,max = 0x3f3f3f3f;
static int n,m,k;
static int[] d = new int[N],back = new int[N];
static Node[] nodes = new Node[M]; // 用来存储结构体
public static void bellman_ford() {
Arrays.fill(d,max); //初始化距离
d[1] = 0; // 初始化起点
for (int i = 0; i < k; i ++) {
back = Arrays.copyOf(d,n + 1); //复制数组
for (int j = 0; j < m; j ++) {
Node node = nodes[j]; //获取每一条边 松弛每一条边
int x = node.x;
int y = node.y;
int z = node.z;
d[y] = Math.min(d[y],back[x] + z); //更新记得用back，防止串联
}
}
if (d[n] > max / 2) System.out.print("impossible"); // 为什么不是 == max,因为松弛操作涉及负权边
else System.out.print(d[n]);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
k = sc.nextInt();
for (int i = 0; i < m; i ++) {
int x = sc.nextInt();
int y = sc.nextInt();
int z = sc.nextInt();
nodes[i] = new Node(x,y,z);
}
bellman_ford();
}
static class Node{
int x;
int y;
int z;
public Node(int x,int y,int z) { // 结构体存在的意义就是方便去更新权值
this.x = x;
this.y = y;
this.z = z;
}
}
}?四、Spfa 算法
spfa 其实是对 bellman-ford 算法进行了优化，我们发现，只有当一个点的距离被更新过，那么它之后的点距离才有可能变小，所以我们可以使用一个队列，先加入起点，然后从队列中取一个点，对这个点的所有边尝试更新，把可以更新的点加入到队列，不断循环直到队列为空，当然，队列中已有的点我们是没必要加入的，因此还需要维持一个st数组
偷大佬一张好图：
1、spfa 的使用场景？
首先肯定是不能存在负环，否则会陷入死循环，其次正权的情况其实也是可以使用 spfa 算法的
例题和代码实现：
给定一个?nn?个点?mm?条边的有向图，图中可能存在重边和自环，?边权可能为负数。
请你求出?11?号点到?nn?号点的最短距离，如果无法从?11?号点走到?nn?号点，则输出?
impossible。数据保证不存在负权回路。
输入格式
第一行包含整数?nn?和?mm。
接下来?mm?行每行包含三个整数?x,y,zx,y,z，表示存在一条从点?xx?到点?yy?的有向边，边长为?zz。
输出格式
输出一个整数，表示?11?号点到?nn?号点的最短距离。
如果路径不存在，则输出?
impossible。数据范围
1≤n,m≤1051≤n,m≤105,
图中涉及边长绝对值均不超过?1000010000。输入样例：
3 3 1 2 5 2 3 -3 1 3 4输出样例：
2
难度：简单 时/空限制：1s / 64MB 总通过数：40024 总尝试数：69847 来源：模板题,AcWing 算法标签 ?
import java.util.*;
public class Main {
static int N = 100010,M = 100010,max = 0x3f3f3f3f;
static int n,m,hh,tt,idx;
static int[] h = new int[N],d = new int[N],e = new int[M],ne = new int[M],w = new int[M];
static int[] q = new int[N];
static boolean[] st = new boolean[N];
public static void add(int a,int b,int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
public static void spfa() {
hh = 0; // 初始化队列
tt = -1;
Arrays.fill(d,max); // 初始化距离数组
d[1] = 0; //固定起点
q[++tt] = 1; //加入队列
st[1] = true;
while (hh <= tt) {
int t = q[hh++]; //每次取出一个点，判断边对应的点能否更新
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if(d[j] > d[t] + w[i]) {
d[j] = d[t] + w[i];
if (!st[j]) {
q[++tt] = j;
st[j] = true; //记得设为true ，不要对队列中已有的重复的点更新
}
}
}
}
if (d[n] == max) System.out.print("impossible");
else System.out.print(d[n]);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Arrays.fill(h,-1);
n = sc.nextInt();
m = sc.nextInt();
for (int i = 0; i < m; i ++) {
int x = sc.nextInt();
int y = sc.nextInt();
int z = sc.nextInt();
add(x,y,z);
}
spfa();
}
}?上边我们提到了 spfa 算法不能应用于有负环的情况，但其实spfa还能用于判断我们一个图中有没有负环的情况
假设我们图中存在负环，那我们寻找最短路的时候一定会重复经过一条边?无数?次，所以当我们遇到经过一个点?到起点的边数大于 n 时（因为n个结点最远的点到起点也最多只有 n - 1 条边），那么这个图中一定存在负环！
import java.util.*;
public class Main{
static int N = 2010,M = 100010,max = 0x3f3f3f3f;
static int n,m,hh,tt,idx;
static int[] h = new int[N],w = new int[M],e = new int[M],ne = new int[M],d = new int[N],cnt = new int[N];
static boolean[] st = new boolean[N];
public static void add(int x,int y,int z){
e[idx] = y;
w[idx] = z;
ne[idx] = h[x];
h[x] = idx++;
}
public static boolean spfa() {
Deque<Integer> q = new LinkedList<>();
for (int i = 1; i <= n; i ++) { //记得把所有的点都加入到队列中 ，因为固定起点有可能导致负环不可达
q.offer(i);
st[i] = true;
}
while(!q.isEmpty()) {
int t = q.poll();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] > d[t] + w[i]) { //唯一不同的地方就是对于每一个点的边数做了统计，如果边数大于n就认为出现负环
d[j] = d[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true;
if (!st[j]) {
q.offer(j);
st[j] = true; //记得设为true
}
}
}
}
return false;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
Arrays.fill(h,-1);
for (int i = 0; i < m ;i ++) {
int x = sc.nextInt();
int y = sc.nextInt();
int z = sc.nextInt();
add(x,y,z);
}
if (spfa()) System.out.print("Yes");
else System.out.print("No");
}
}1、为什么没有对d数组初始化为最大值？这不会导致后面d【j】 > d【j】?+ w【i】判断出错吗？
是的，对于正权边来说，他没有更新为最短路，但我们此时要求的是判断有无负环，正权边对我们没有影响，我们只需要保证负权边即使在没有初始化的情况下也能更新即可
?2、为什么此时不使用静态链表模拟队列了？
其实此处不使用静态链表模拟队列是因为我们会重复的往队列里加入结点，但你开2 * N 其实也完全够用
五、Floyd 算法
?floyed 的算法实现非常简单，三层循环，每次更新边就好了
import java.util.*;
public class Main{
static int N = 210,M = 20010,max = 0x3f3f3f3f;
static int n,m,k;
static int[][] g = new int[N][N];
public static void floyd() {
for (int k = 1; k <= n; k ++) {
for (int j = 1; j <= n; j ++) {
for (int i = 1; i <= n; i ++) {
g[i][j] = Math.min(g[i][j],g[i][k] + g[k][j]);
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
k = sc.nextInt();
for (int i = 1; i <= n; i ++) { //自己到自己是0 ，其他边都是无穷大
for (int j = 1; j <= n; j ++) {
if (i == j) g[i][j] = 0;
else g[i][j] =max;
}
}
for (int i = 0; i < m; i ++) {
int x = sc.nextInt();
int y = sc.nextInt();
int z = sc.nextInt();
g[x][y] = Math.min(g[x][y],z); //由于会出现重边，所以选最小的权值
}
floyd();
while(k-- > 0) {
int x = sc.nextInt();
int y = sc.nextInt();
int t = g[x][y];
if (t > max / 2) System.out.println("impossible"); //更新两个点的距离时，可能会出现负权导致无穷大稍微少一点
else System.out.println(t);
}
}
}floyd 其实是基于动态规划的，可能到后边会证明吧。。。。。。
1、重边的处理方式？
通过上边几种方法我们可以看到，要是使用邻接矩阵，那么我们就默默的选择最小的权值就行了，否则我们其实都是有对应的处理方式的，堆优化dijkstra 优先使用的是权值最小的边，bellman-ford 算法 是要经过所有的边，所以重边其实没有影响，spfa 算法重边较小权值的那个一定会更新，导致后边一连串的更新
2、环的处理方式？
环的处理其实很粗暴，如果不是负环，那么正环在更新最短路时一定会被舍弃（因为它一定不是最短路）