扩展卡尔曼滤波 (EKF)

EKF之雅克比矩阵

文章目录

扩展卡尔曼滤波 (EKF)
前言
一、什么是线性化？
二、雅克比矩阵
三、工程中雅克比矩阵如何应用
总结

前言

一般的卡尔曼滤波（KF），是假设系统模型是线性的，即系统的输入输出满足齐次性和叠加性。标准卡尔曼滤波的前提条件之一，就是高斯分布的x_k 预测后仍服从高斯分布，高斯分布的x_k 变换到观测空间后仍服从高斯分布因此标准卡尔曼滤波只适合线性系统的处理。

但是实际工程中，卡尔曼滤波一般用于对传感器，电机等电子器件。这些期间由于电子性质，自身特性，基本都是非线性的，那么在这个系统之上建立的所有模型，都符合非线性系统。

如何将一个非线性系统线性化，就是EKF改进的部分。

一、什么是线性化？

请大家看下面这个圆：
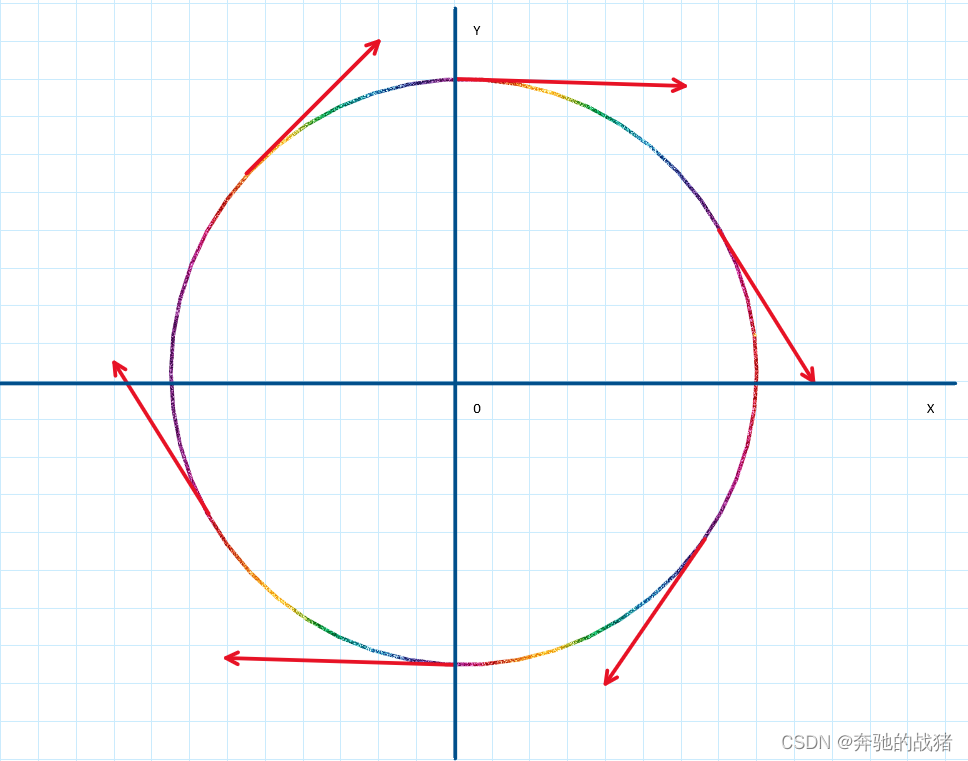
在这里插入图片描述
一个平平无奇的圆，其方程一般式如下：

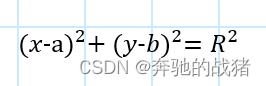
其方程式是一个明显的非线性函数，看圆的形状也能看出来。图中也画出来了几个红色箭头，指向的方向圆在某一点的切线方向。这个方向没有弯曲，笔直的打出去，那么在这个切线处，圆是一条直线？我们随意找一个切线然后放大：

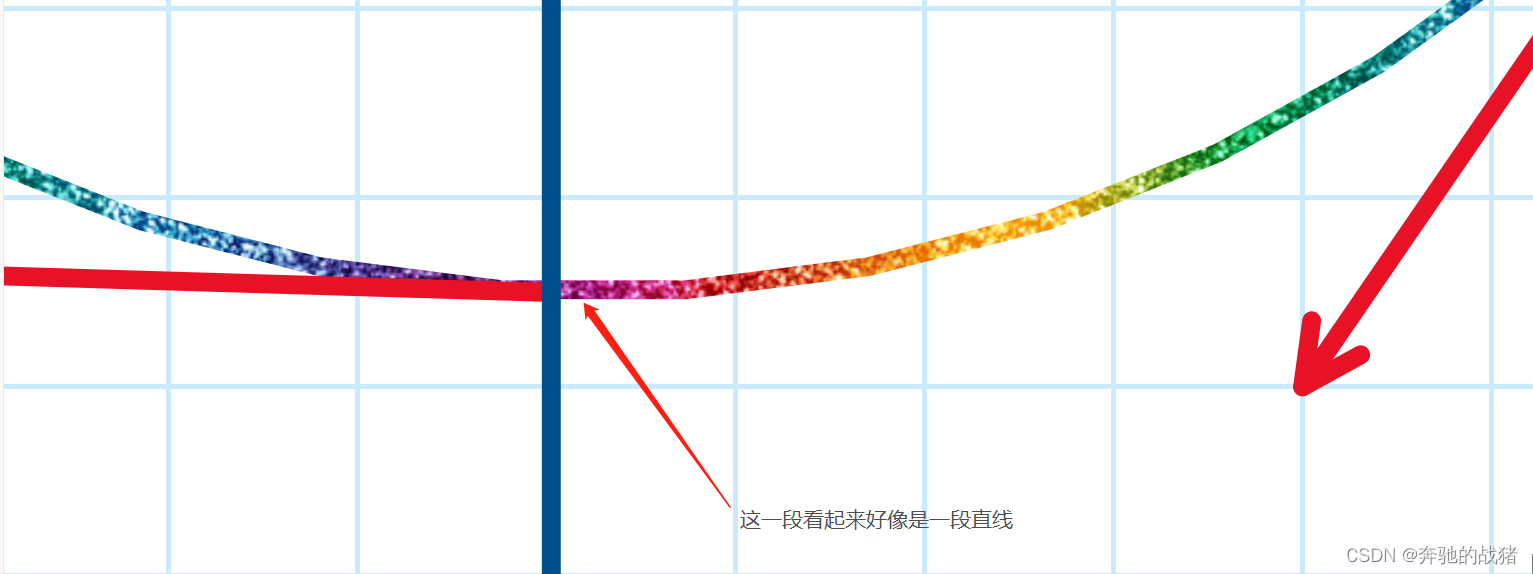
在这里插入图片描述
原谅我这个放大倍率已经是OneNote的极限的，可以明显看到，放大后的圆，在切线处这一小段直线，貌似是线性的。那么是否只要求出这个小小的线段的方程式，我们就能把圆在这个点局部线性化了！

这个方法直接告诉大家，就是求圆在这个点处的导数，即可得出这个小小的线段的方程式了。这就是一种局部线性化的方式。

而在卡尔曼滤波中，一切数据传递，计算，更新都是通过矩阵来完成，怎么把一个矩阵线局部线性化呢？通过求该矩阵的雅克比矩阵即可。

二、雅克比矩阵

雅克比矩阵的概念我是从可汗学院看来的，有兴趣大家可以移步b站看熟肉：
可汗学院雅克比矩阵
下面介绍下我印象比较深的几个点：

1.矩阵的几何含义

已知一个矩阵 A =
$\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right] \tag{1}$

他在笛卡尔坐标系下的几何含义为：
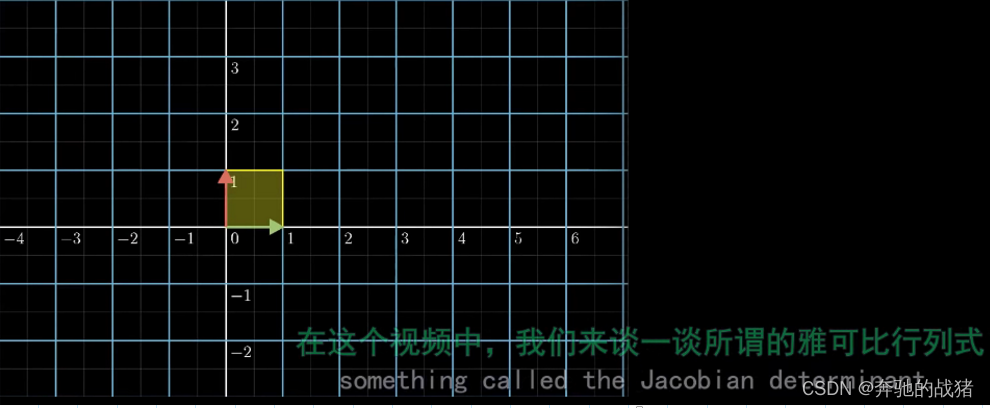
在这里插入图片描述
一个小矩形，沿x方向和沿y方向均有分量。

假设有另一个矩阵 B =
$\left[ \begin{matrix} 3 & 1 \\ 0 & 2 \\ \end{matrix} \right] \tag{2}$
通过矩阵行列式可以算出该矩阵的标量，其几何含义为向量[3,0]和向量[1,2]所围成的面积
我们将矩阵B做一个线性变化：

del(B) = 3 * 2 - 1 * 0 = 6

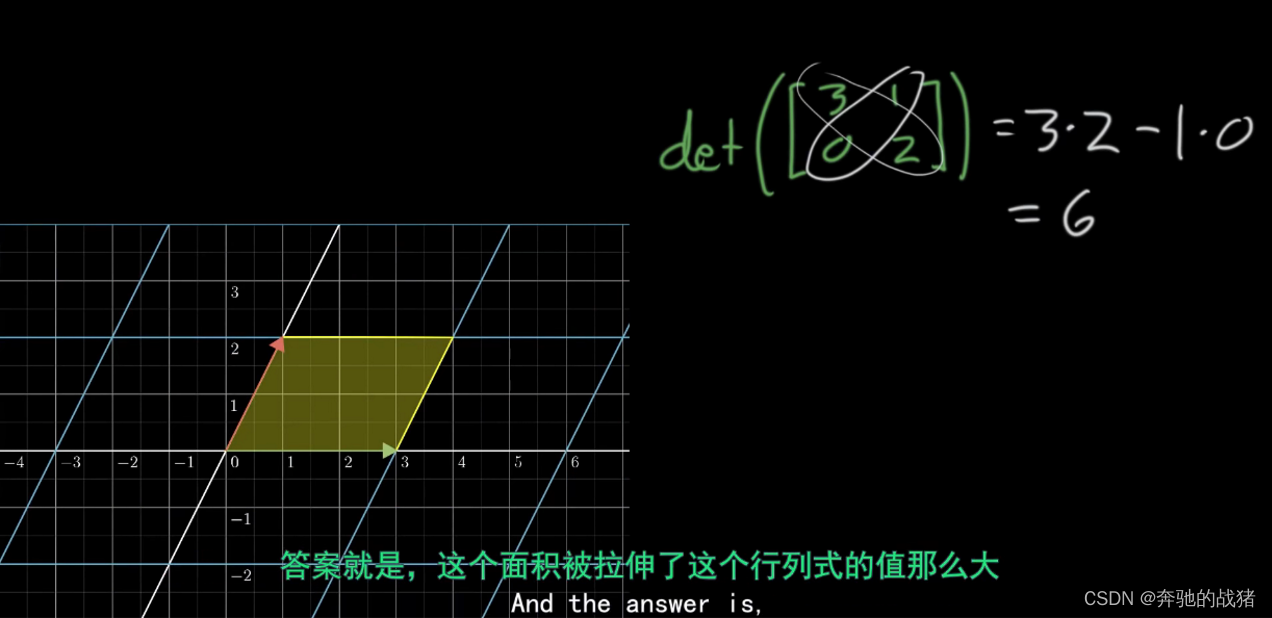
在这里插入图片描述
如果把上面的矩阵 A 的面积为1，如果我们把矩阵 A看做是基底，那么矩阵B就是基底的6倍，这样，我们就可以把不同矩阵的几何意义联系在了一起。

但是我们能看出来，矩阵A到矩阵B是一个很标准的线性关系，那如果存在一组多元函数，且该函数呈现非线性关系，那么如何从几何层面理解这个多元函数与基底的关系呢？

2.非线性矩阵与基底的关系

假设有一个矩阵C =

$\left[ \begin{matrix} f1(x,y) \\ f2(x,y) \\ \end{matrix} \right] \tag{3}$

$\left[ \begin{matrix} x + sin(y) \\ y + sin(x) \\ \end{matrix} \right] \tag{4}$

这个矩阵是个非常典型的非线性矩阵，下面将坐标系中的所有（x,y）均乘以该矩阵，即将该坐标系中的所有点均转换成矩阵C下的点，抓住其中一个小矩形放大：
在这里插入图片描述
这里怎么理解呢？就是维持原有坐标系不变，将坐标系中每个点通过矩阵C转移到新的地方，矩阵C可以当成一个状态转移矩阵。转移后把每个点可视化出来，即可得到上图扭曲的图形，看起来和线性化根本不搭。

但是当对某一个区域放大时，可以看到虽然新图形围城的小矩形不那么方正，但是也没有变得特别扭曲，这个小矩形和基底之间的关系，就是其非线性化的程度。把这个区域再放大，那么其形状越接近基底。这就说明新图形的整体是非线性的，但是对局部而言，仍可以看做是线性的。放大倍率越大，其线性化程度越好。

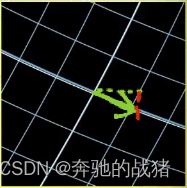
在这里插入图片描述
(如上图经过局部放大后?x默认为无穷小，对x求偏导就可以把这个无穷小量化成正常的函数在x这个方向上的变化率。上图的基底是正交坐标系，放大以后，朝着x方向的伸缩能够正交分解成两个维度的变化率，同理y方向也是一样的，由此性质，可以推出矩阵C的雅可比矩阵D)

3.雅克比矩阵

根据上面对圆的局部线性化的推导，我们只要求出矩阵C导数，就可以得出矩阵C的雅克比矩阵D了。一个矩阵是多维度的，我们对这个矩阵的每一个维度求偏导，如矩阵C存在二维（x,y），那么只需要求矩阵C对于x的偏导，对于y的偏导，即可推出雅克比矩阵。

CSDN打公式太麻烦了，下面直接上图：
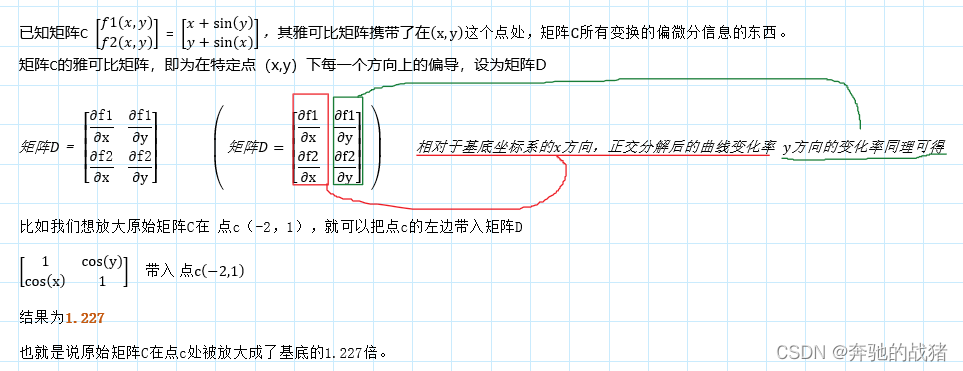
在这里插入图片描述

三、工程中雅克比矩阵如何应用

卡尔曼滤波中，需要对系统建模，根据模型推导状态转移矩阵F和更新矩阵H，通常还有个控制矩阵U不过这个不常用，一般通过状态空间对系统建模，太细就先不讲。

EKF中需要非线性化的就是矩阵F和矩阵H，这两个矩阵分别用于协方差矩阵Pk的更新和卡尔曼系数Kk的更新。
前面说了，矩阵有多个维度，对卡尔曼这个系统而言，每个状态向量X = [x1,x2,x3,x4, … , xn]都是一个维度，那么就需要矩阵F对于矩阵X求偏导，矩阵H对于矩阵X求偏导。

F(x1,x2,x3,x4) =

$\left[ \begin{matrix} f1(x1,x2,x3,x4) \\ f2(x1,x2,x3,x4) \\ f3(x1,x2,x3,x4) \\ f4(x1,x2,x3,x4) \\ \end{matrix} \right] \tag{5}$

JF =
$\left[ \begin{matrix} ?f1/?x1 & ?f1/?x2 & ?f1/?x3 & ?f1/?x4 \\ ?f2/?x1 & ?f2/?x2 & ?f2/?x3 & ?f2/?x4 \\ ?f3/?x1 & ?f3/?x2 & ?f3/?x3 & ?f3/?x4 \\ ?f4/?x1 & ?f4/?x2 & ?f4/?x3 & ?f4/?x4 \\ \end{matrix} \right] \tag{6}$