您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入?x?数
- 删除?x?数(若有多个相同的数,因只删除一个)
- 查询?x?数的排名(排名定义为比当前数小的数的个数?+1?)
- 查询排名为?x?的数
- 求?x?的前驱(前驱定义为小于?x,且最大的数)
- 求?x?的后继(后继定义为大于?x,且最小的数)
一、红黑树定义
红黑树的英文是“Red-Black Tree”,简称 R-B Tree,它是一种不严格的平衡二叉查找树
二叉查找树这一数据结构并不难,而红黑树之所以难是难在它是自平衡的二叉查找树,在进行插入和删除等可能会破坏树的平衡的操作时,需要重新自处理达到平衡状态。
红黑树是一种含有红色和黑色节点并能自平衡的二叉查找树,红黑树和其他二叉查找树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的性质,从而获得较高的查找性能。它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的:它可以在 O(log n) 时间内做查找,插入和删除,这里的 n 是树中元素的数目。
二、红黑树性质
红黑树是一颗二叉搜索树,它在每一个结点上增加了一个储存位来表示结点的颜色,可以是RED或BLACK。通过对任何一条从根到叶子的简单路径上的各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出两倍,因而是近似平衡的。
树中每个结点包含5个属性:color、key、left、right、p。如果一个结点没有子结点或父结点,则该结点相应指针属性的值为NIL.我们可以把这些NIL视为指向二叉搜索树的叶结点(外部结点)的指针,而把带关键字的结点视为树的内部结点。
一颗红黑树是满足下面红黑性质的二叉搜索树:
性质1:每个结点是红色或黑色。
性质2:根结点是黑色。
性质3:每个叶结点(NIL)是黑色的。
性质4:如果一个结点是红色的,则它的两个子结点都是黑色的。
性质5:对每个结点,从该结点到其后代叶结点的简单路径上,均包含相同数目的黑色结点。
为了便于处理红黑树代码中的边界条件,使用一个哨兵来代表NIL.对于一颗红黑树T,哨兵T.nil是一个与树中普通结点有相同属性的对象。它的color属性为BLACK,而其他属性p、left、right和key可以设为任意值。所有指向NIL的指针都用指向哨兵T.nil的指针替换。
结点类代码如下
class Node{
private:
pair<T,V> p;
int s;
bool color;//0代表红色 1代表黑色
Node* Lt;
Node* Rt;
Node* pre;
public:
Node(pair<T,V> _p,int _s,bool _color,Node* _Lt = nullptr,Node* _Rt = nullptr,Node* _pre = nullptr):
p(_p),s(_s),color(_color),Lt(_Lt),Rt(_Rt),pre(_pre){}
Node(Node* tmp):p(tmp->p),s(tmp->s),color(tmp->color),Lt(tmp->Lt),Rt(tmp->Rt),pre(tmp->pre){}
Node*& GetLt() { return Lt;}
Node*& GetRt() { return Rt;}
Node*& Getpre() { return pre;}
T& Getdata() { return p.first;}
V& Getinfo() { return p.second;}
pair<T,V>* Getpair(){ return &p;}
bool Getcolor() const{ return color;}
int& Getsize() { return s;}
void SetLt(Node*& tmp){Lt = tmp;}
void SetRt(Node*& tmp){ Rt = tmp;}
void Setpre(Node*& tmp){ pre = tmp;}
void Setdata(T tmp){ p.first = tmp;}
void Setinfo(V tmp){ p.second = tmp;}
void Setcolor(bool tmp){ color = tmp;}
};三、红黑树的相关操作
在插入、删除节点的过程中,性质3、性质4可能会被破坏,为了维护这些性质,必须要改变树中某些结点的颜色以及指针结构。
指针结构的修改是通过旋转(ratation)来完成的,分为左旋和右旋。
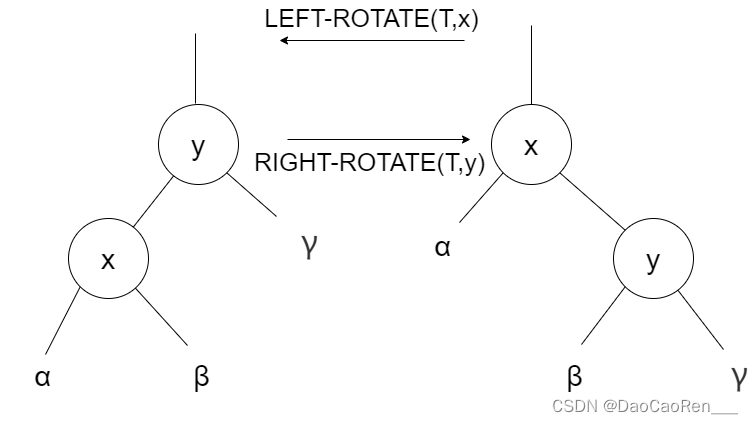
?
左旋以x到y的链为“支轴”进行。它使y成为该子树新的根节点,x成为y的右孩子,y的左孩子成为x的右孩子。
左旋、右旋代码:
void LRotate(Node* x){//左旋
Node* tmp = Rt(x); //tmp为x的右结点
x->SetRt(Lt(tmp)); //让tmp的左结点作为x的右结点
if(Lt(tmp) != nil) Lt(tmp)->Setpre(x);
tmp->Setpre(pre(x)); //让x的父结点作为tmp的父结点
if(pre(x) == nil) root = tmp; //如果x是根结点,更新根结点为tmp
else{ //如果x是左结点,则让tmp为左结点,如果x是右结点,则让tmp为右结点
if(Lt(pre(x)) == x) pre(x)->SetLt(tmp);
else pre(x)->SetRt(tmp);
}
tmp->SetLt(x); //让x作为tmp的左结点
x->Setpre(tmp); //让tmp作为x的父结点
x->Getsize() = 1;
if(x->GetLt() != nil) x->Getsize() += x->GetLt()->Getsize();
if(x->GetRt() != nil) x->Getsize() += x->GetRt()->Getsize();
tmp->Getsize() = x->Getsize() + 1;
if(tmp->GetRt() != nil) tmp->Getsize() += tmp->GetRt()->Getsize();
}
void RRotate(Node* x){
Node* tmp = Lt(x);
x->SetLt(Rt(tmp));
if(Rt(tmp) != nil) Rt(tmp)->Setpre(x);
tmp->Setpre(pre(x));
if(pre(x) == nil) root = tmp;
else{
if(Rt(pre(x)) == x) pre(x)->SetRt(tmp);
else pre(x)->SetLt(tmp);
}
tmp->SetRt(x);
x->Setpre(tmp);
x->Getsize() = 1;
if(x->GetLt() != nil) x->Getsize() += x->GetLt()->Getsize();
if(x->GetRt() != nil) x->Getsize() += x->GetRt()->Getsize();
tmp->Getsize() = x->Getsize() + 1;
if(tmp->GetLt() != nil) tmp->Getsize() += tmp->GetLt()->Getsize();
}红黑树的插入
插入结点的颜色为红色(插入结点的颜色为黑色,可能破坏性质四,插入结点为红色,可能破坏性质三,但修复性质三的代价比修复性质四的代价小,所以选择插入结点的颜色为红色)
第一步:?我们先按照二叉搜索树树插入节点的方式,插入节点
第二步:?为了不破坏红黑树的规则,我们插入节点后要对红黑树进行相应的调整
下面分两种情况
第一种情况:?如果插入节点的父亲是黑色节点,那么可以直接结束,不需要继续调整了(没有破坏红黑树的基本性质)
第二种情况:?如果插入节点为的父亲为红色节点,就需要进行相应的调整(性质4被破坏)
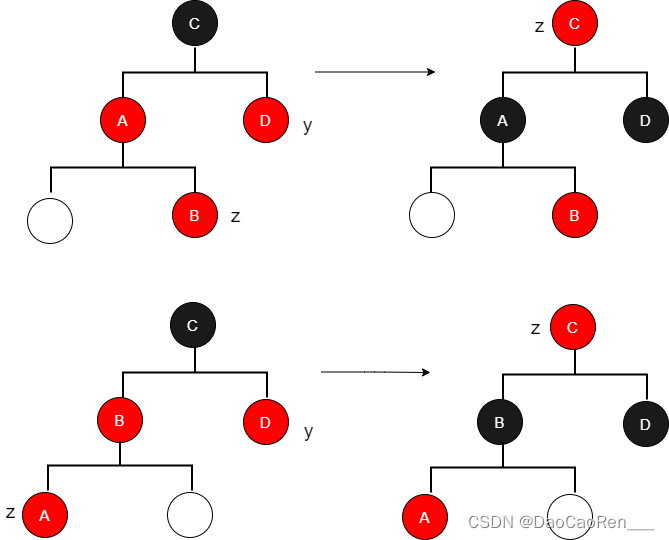
?
上图为调整情况1:z的叔结点y是红色的
这种情况在z.p和y都是红色时发生。因为z.p.p是黑色的,所以将z.p和y都着为黑色,以此解决z和z.p都是红色的问题,将z.p.p着为红色一保持性质5。然后,把z.p.p作为新结点z来重复修正被破坏的性质,直到所有性质都满足。指针z在树中上移两层。
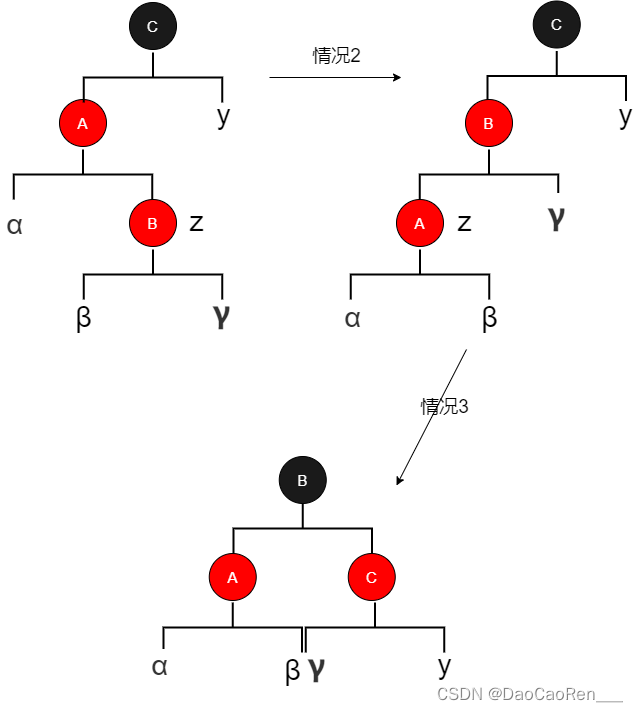
?
情况2:z的叔结点y是黑色的且z是一个右孩子
情况3:z的叔结点y是黑色的且z是一个左孩子
在情况2和情况3中,z的叔结点y是黑色的,通过z是z.p的右孩子还是左孩子来区别这两种情况。在情况2中,结点z是它父结点的右孩子,可以使用一个左旋来将此情形转变为情况3,此时结点z为左孩子。因为z和z.p都是红色的,所以该旋转对性质无影响。无论是直接进入情况3,还是通过情况2进入情况3,z的叔结点y总是是黑色的,否则就要执行情况1。在情况3中,改变某些结点的颜色并做一次右旋,以保持性质5。这样由于不再有两个红色结点相邻,所有处理到处完毕。因为此时z.p是黑色的,无需再进行循环。
插入代码如下:
void Insert(pair<T,V> p)
{
Node* y = nil;
Node* x = root;
Node* z = new Node(p,0,nil,nil,nil); //z为要插入的结点
while(x != nil){ //寻找插入的位置
y = x;
if(p.first < x->Getdata()) x = Lt(x);
else x = Rt(x);
}
z->Setpre(y); //让y作为z的父结点
if(y == nil) root = z; //如果树为空,则z为根结点
else if(z->Getdata() < y->Getdata()){ //如果z的key比y的key小,则z为y的左结点,否则为右 结点
y->SetLt(z);
}
else y->SetRt(z);
z->SetLt(nil);
z->SetRt(nil);
z->Setcolor(0);
FixAfterInsert(z); //插入之后的调整
}
void FixAfterInsert(Node* z){
while(color(z->Getpre()) == 0){ //如果z的父结点为红色,进入循环,否则结束循环
if(pre(z) == Lt(pre(pre(z)))){ //如果z的父结点是z的祖父结点的左结点
Node* y = Rt(pre(pre(z))); //y为z的叔结点
if(color(y) == 0){ //如果y结点为红色进入情况1
pre(z)->Setcolor(1); //case1 将z的父节点的颜色改为黑色
y->Setcolor(1); //case1 将y的颜色改为黑色
pre(pre(z))->Setcolor(0); //case1 将祖父结点的颜色改为红色
z = pre(pre(z)); //case1 将指针z上移两层
continue; //进行下一次循环
} //y结点为黑色的情况
if(z == Rt(pre(z))){ //case2 如果z是其父结点的右结点
z = pre(z); //case2 对z的父结点做左旋
LRotate(z); //case2 左旋之后z结点的key和val不变,只是右结点和父结点变了
}
pre(z)->Setcolor(1); //case3 将z的父结点的颜色改为黑色
pre(pre(z))->Setcolor(0); //case3 将z的祖父结点的颜色改为红色
RRotate(pre(pre(z))); //case3 对z的祖父结点右旋
}
else{ //z的父结点是z的祖父结点的y右结点的情况,与z的父结点是z的祖父结点的y左结点的情况对称
Node* y = Lt(pre(pre(z)));
if(color(y) == 0){
pre(z)->Setcolor(1); //case1
y->Setcolor(1); //case1
pre(pre(z))->Setcolor(0); //case1
z = pre(pre(z)); //case1
continue;
}
if(z == Lt(pre(z))){ //case2
z = pre(z); //case2
RRotate(z); //case2
}
pre(z)->Setcolor(1); //case3
pre(pre(z))->Setcolor(0); //case3
LRotate(pre(pre(z))); //case3
}
}
root->Setcolor(1); //循环过程中有可能修改根结点的颜色,要保持根结点为黑色
}红黑树的删除
与插入操作相比,删除操作要稍微麻烦一些。
首先要设计一个删除过程中要使用到的替换函数transplant,代码如下:
void transplant(Node* u,Node* v){
if(pre(u) == nil) root = v; //如果u是根结点,则让v为根结点
else if(u == Lt(pre(u))) pre(u)->SetLt(v); //如果u是左结点,则让v为左结点
else pre(u)->SetRt(v); //如果u是右结点,则让v为右结点
v->Setpre(pre(u)); //让u的父结点作为v的父结点
}还要设计一个寻找key值最小的结点的函数minimum,代码如下:
Node* minimum(Node* x){
if(x == nil) return x;
while(Lt(x) != nil){
x->Getsize()--; //删除时要维护size大小
x = Lt(x);
}
return x;
}下面进入删除:
删除一个结点之后为了维护二叉搜索树的性质,需要找一个结点来替代删除结点的位置
第一步:?我们先按照二叉搜索树树删除节点的方式,删除节点
第二步:?为了不破坏红黑树的规则,我们删除节点后要对红黑树进行相应的调整
下面分两种情况:
第一种情况:删除的结点有一个左结点或一个右结点不是叶结点,或左右结点都是叶结点。
如果左右结点都是叶结点则用叶结点替换要删除的结点。如果删除的结点有一个左结点或一个右结点不是叶结点,则用非叶结点替换要删除的结点。
第二种情况:删除的结点没有叶结点。
用删除结点的后继结点替换删除的结点,后继结点是大于该结点且最小的结点。以删除结点的右结点为根结点的树中的最小结点就是删除结点的后继结点。由于后继结点替代了删除结点,后继结点也需要有结点替代,由于后继结点没有左结点,则后继结点的替代结点就是它的右结点。此时,有一种特殊情况,当删除结点的后继结点就是删除结点的右结点时,后继结点无需替代结点。
如果删除的是黑色结点,则需要调整(破坏了性质5)。
调整的情况:
蓝色表示可以是红色也可以是黑色
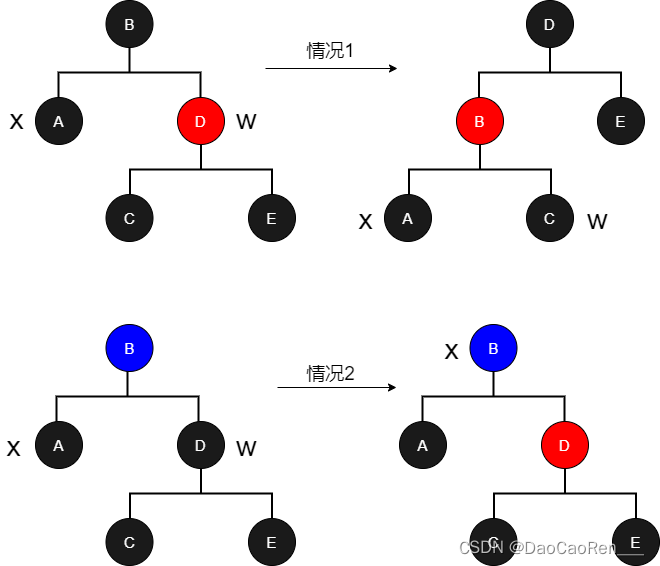
 ?
?
情况1:x的兄弟结点w是红色的
因为w必须有黑色子结点,所以可以改变w的x.p的颜色,然后对x.p做一次左旋而不违反红黑树的任何性质。现在,x的新兄弟结点是旋转之前的w的某个子结点,其颜色为黑色。这样就将情况1转换为情况2、3或4处理。
当结点w为黑色时,属于情况2、3和4;这些情况是由w的子结点的颜色来区分的。
情况2:x的兄弟结点w是黑色的,而且w的两个子结点都是黑色的
因为w的颜色是黑色的,所以在删除x结点时将w的颜色改为红色,这样B结点的左子树和右子树中都少了一个黑色结点。如果B结点是红色的,则退出循环,让B结点的颜色为黑色,补偿一个黑色结点。如果B结点是黑色的,B结点无法补偿一个黑色结点,则等效删除了一个黑色结点,B结点为删除结点的替代结点,继续循环。
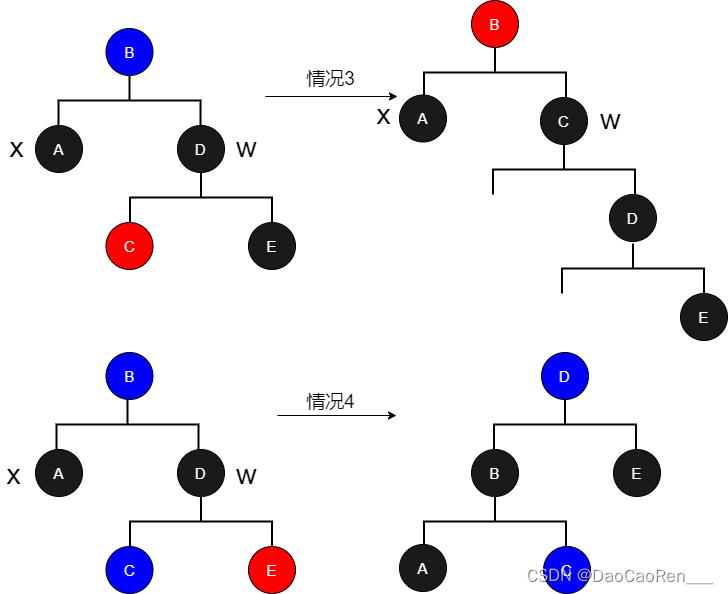
情况3:x的兄弟结点w是黑色的,w的左结点是红色的,w的右结点是黑色的
可以交换w和w的左结点的颜色,然后对w进行右旋而不违反红黑树的任何性质。现在x的新兄弟结点w是一个有右孩子的黑色结点,这样就将情况3转换成了情况4。
情况4:x的兄弟结点w是黑色的,且w的右结点是红色的
可以交换B和w的颜色,并让E的颜色为黑色,然后对B进行一次左旋,这样删除x结点之后红黑树的性质没有被破坏。因为旋转前x结点的黑高等于C结点的黑高加一,所以在删除x结点之后,B的左子树的黑高等于右子树的黑高。旋转后B的黑高等于旋转前D的黑高(旋转后的B与旋转前的D都有相同的子树C)等于旋转前E的黑高,而旋转前E的黑高等于旋转后E的黑高,所以旋转后B的黑高和旋转后E的黑高相等,旋转前B的黑高等于旋转前E的黑高加一,旋转后D的黑高等于E的黑高加一,所以旋转前B的黑高等于旋转后D的黑高。所以红黑树的性质没有被破坏。这时应该把x置为根结点,以结束循环。
删除代码如下:
bool Delete(Node* z){
Node* y = z; //y为z的替代结点
int yoc = color(y); //记录y的颜色
Node* x = z; //x为y的替代结点
if(Lt(z) == nil){ //z有两个叶结点或左结点为叶结点
x = Rt(z);
transplant(z,Rt(z)); //用z的右结点替换z
}
else if(Rt(z) == nil){ //z的右结点为叶结点
x = Lt(z);
transplant(z,Lt(z)); //用z的左结点替换z
}
else{ //z没有叶结点
y = minimum(Rt(z)); //让y为z的后继结点
yoc = color(y); //记录y的颜色
x = Rt(y); //让x为y的右结点
if(pre(y) == z){ //判断特殊情况
x->Setpre(y);
}
else{ //当y不是z的右结点时
transplant(y,Rt(y)); //用y的右结点替换y
y->SetRt(Rt(z)); //把z的右结点作为y右结点
Rt(y)->Setpre(y);
}
transplant(z,y); // 用y替换z
y->SetLt(Lt(z)); //把z的左结点作为y的左结点
Lt(y)->Setpre(y);
y->Setcolor(color(z)); //把y的颜色改为z的颜色
}
delete z;
if(yoc == 1){ //当删除结点为黑色时,需要调整
FixAfterDelete(x);
}
return true;
}
bool Delete(T val){
Node* tmp = this->root;
while(tmp != nil){ //寻找要删除的结点
if(tmp->Getdata() > val){
tmp = tmp->GetLt();
}
else if(tmp->Getdata() < val){
tmp = tmp->GetRt();
}
else break;
}
if(tmp == nil){ //没有找到
return false;
}
else{
return Delete(tmp);
}
}
void FixAfterDelete(Node* x){
while(x != root && color(x) == 1){ //当x不为根结点或x的颜色为黑色
if(Lt(pre(x)) == x){ //如果x的左结点
Node* w = Rt(pre(x)); //w是x的兄弟结点
if(color(w) == 0){ //如果w的颜色为红色
w->Setcolor(1); //case1 让w的颜色为黑色
pre(x)->Setcolor(0); //case1 让x的父结点的颜色为红色
LRotate(pre(x)); //case1 对x的父结点左旋
w = Rt(pre(x)); //case1 更新兄弟结点
}
if(color(Lt(w)) == 1 && color(Rt(w)) == 1){ //如果w有两个黑色子结点
w->Setcolor(0); //case2 //让w的颜色为红色
x = pre(x); //case2 //让x为x的父节点
}
else{
if(color(Rt(w)) == 1){ //如果w的右结点为黑色
Lt(w)->Setcolor(1); //case3 让w的左结点的颜色为黑色
w->Setcolor(0); //case3 让w的颜色为红色
RRotate(w); //case3 对w进行右旋
w = Rt(pre(x)); //case3 更新兄弟结点
}
w->Setcolor(color(pre(x))); //case4 让w和x的父结点交换颜色
pre(x)->Setcolor(1); //case4 让x的父结点的颜色为黑色
Rt(w)->Setcolor(1); //case4 让w的右结点的颜色为黑色
LRotate(pre(x)); //case4 对x的父结点进行左旋
x = root; //case4 让x成为根结点,结束循环
}
}
else{ //x是右结点的情况 与x是左结点的情况对称
Node* w = Lt(pre(x));
if(color(w) == 0){
w->Setcolor(1); //case1
pre(x)->Setcolor(0); //case1
RRotate(pre(x)); //case1
w = Lt(pre(x)); //case1
}
if(color(Lt(w)) == 1 && color(Rt(w)) == 1){
w->Setcolor(0); //case2
x = pre(x); //case2
}
else{
if(color(Lt(w)) == 1){
Rt(w)->Setcolor(1); //case3
w->Setcolor(0); //case3
LRotate(w); //case3
w = Lt(pre(x)); //case3
}
w->Setcolor(color(pre(x))); //case4
pre(x)->Setcolor(1); //case4
Lt(w)->Setcolor(1); //case4
RRotate(pre(x)); //case4
x = root; //case4
}
}
}
x->Setcolor(1);
}前驱、后继:
Node* Lt_node(Node* x){ //前驱
Node* tmp = x;
if(tmp->GetLt() == nil){
while(tmp->Getpre() != nil && tmp->Getpre()->GetLt() == tmp){
tmp = tmp->Getpre();
}
tmp = tmp->Getpre();
}
else{
tmp = tmp->GetLt();
while(tmp->GetRt() != nil){
tmp = tmp->GetRt();
}
}
return tmp;
}
Node* Rt_node(Node* x){ //后继
Node* tmp = x;
if(tmp->GetRt() == nil){
while(tmp->Getpre() != nil && tmp->Getpre()->GetRt() == tmp){
tmp = tmp->Getpre();
}
tmp = tmp->Getpre();
}
else{
tmp = tmp->GetRt();
while(tmp->GetLt() != nil){
tmp = tmp->GetLt();
}
}
return tmp;
}
Node* Lfind(T key){ //key不一定在树中,所以要分类
Node* parent = nil;
Node* current = root;
Node* t = nil;
while(current != nil){//当当前节点不为空时 寻找结点
if(current->Getdata() > key){
parent = current;
current = current->GetLt();
}
else if(current->Getdata() < key){
parent = current;
current = current->GetRt();
}
else{
t = Lt_node(current);
break;
}
}
if(current->Getdata() == key){ //处理同值的情况
while(t->Getdata() == key){
t = Lt_node(t);
}
return t;
}
if(parent->Getdata() > key){
return Lt_node(parent);
}
else{
return parent;
}
}
Node* Rfind(T key){
Node* parent = nil;
Node* current = root;
Node* t = nil;
while(current != nil){//当当前节点不为空时
if(current->Getdata() > key){
parent = current;
current = current->GetLt();
}
else if(current->Getdata() < key){
parent = current;
current = current->GetRt();
}
else{
t = Rt_node(current);
break;
}
}
if(current->Getdata() == key){
while(t->Getdata() == key){
t = Rt_node(t);
}
return t;
}
if(parent->Getdata() < key){
return Rt_node(parent);
}
else{
return parent;
}
}寻找第k大、查找排名(相同结点不合并版本)
Node* findkth(int k,Node* p){
if(p->GetLt() == nil){
if(k == 1){
return p;
}
else{
return findkth(k-1,p->GetRt());
}
}
else{
if(p->GetLt()->Getsize() == k-1) return p;
else if(p->GetLt()->Getsize() >= k) return findkth(k,p->GetLt());
else return findkth(k-p->GetLt()->Getsize()-1,p->GetRt());
}
}
int find_rank(T v,Node* p){
if(p == nil) return 1;
else if(p->Getdata() >= v) return find_rank(v,p->GetLt());
else return (1 + (p->GetLt() ? p->GetLt()->Getsize() : 0 ) + find_rank(v,p->GetRt()));
}完整代码:
#include <bits/stdc++.h>
using namespace std;
#define RED 0 //红色结点
#define BLACK 1 //黑色结点
template<typename T,typename V>
class redblacktree{
private:
class Node{
private:
pair<T,V> p;
int s;
bool color;//0代表红色 1代表黑色
Node* Lt;
Node* Rt;
Node* pre;
public:
Node(pair<T,V> _p,int _s,bool _color,Node* _Lt = nullptr,Node* _Rt = nullptr,Node* _pre = nullptr):
p(_p),s(_s),color(_color),Lt(_Lt),Rt(_Rt),pre(_pre){}
Node(Node* tmp):p(tmp->p),s(tmp->s),color(tmp->color),Lt(tmp->Lt),Rt(tmp->Rt),pre(tmp->pre){}
Node*& GetLt() { return Lt;}
Node*& GetRt() { return Rt;}
Node*& Getpre() { return pre;}
T& Getdata() { return p.first;}
V& Getinfo() { return p.second;}
pair<T,V>* Getpair(){ return &p;}
bool Getcolor() const{ return color;}
int& Getsize() { return s;}
void SetLt(Node*& tmp){Lt = tmp;}
void SetRt(Node*& tmp){ Rt = tmp;}
void Setpre(Node*& tmp){ pre = tmp;}
void Setdata(T tmp){ p.first = tmp;}
void Setinfo(V tmp){ p.second = tmp;}
void Setcolor(bool tmp){ color = tmp;}
};
bool color(Node* node){
if(node == nil) return true;
else return node->Getcolor();
}
void Setcolor(Node* node,bool col){
node->Setcolor(col);
}
Node*& pre(Node* node){
return node->Getpre();
}
Node*& Lt(Node* node){
return node->GetLt();
}
Node*& Rt(Node* node){
return node->GetRt();
}
void LRotate(Node* x){//左旋
Node* tmp = Rt(x);
x->SetRt(Lt(tmp));
if(Lt(tmp) != nil) Lt(tmp)->Setpre(x);
tmp->Setpre(pre(x));
if(pre(x) == nil) root = tmp;
else{
if(Lt(pre(x)) == x) pre(x)->SetLt(tmp);
else pre(x)->SetRt(tmp);
}
tmp->SetLt(x);
x->Setpre(tmp);
x->Getsize() = 1;
if(x->GetLt() != nil) x->Getsize() += x->GetLt()->Getsize();
if(x->GetRt() != nil) x->Getsize() += x->GetRt()->Getsize();
tmp->Getsize() = x->Getsize() + 1;
if(tmp->GetRt() != nil) tmp->Getsize() += tmp->GetRt()->Getsize();
}
void RRotate(Node* x){
Node* tmp = Lt(x);
x->SetLt(Rt(tmp));
if(Rt(tmp) != nil) Rt(tmp)->Setpre(x);
tmp->Setpre(pre(x));
if(pre(x) == nil) root = tmp;
else{
if(Rt(pre(x)) == x) pre(x)->SetRt(tmp);
else pre(x)->SetLt(tmp);
}
tmp->SetRt(x);
x->Setpre(tmp);
x->Getsize() = 1;
if(x->GetLt() != nil) x->Getsize() += x->GetLt()->Getsize();
if(x->GetRt() != nil) x->Getsize() += x->GetRt()->Getsize();
tmp->Getsize() = x->Getsize() + 1;
if(tmp->GetLt() != nil) tmp->Getsize() += tmp->GetLt()->Getsize();
}
void transplant(Node* u,Node* v){
if(pre(u) == nil) root = v;
else if(u == Lt(pre(u))) pre(u)->SetLt(v);
else pre(u)->SetRt(v);
v->Setpre(pre(u));
}
Node* minimum(Node* x){
if(x == nil) return x;
while(Lt(x) != nil){
x->Getsize()--;
x = Lt(x);
}
return x;
}
Node* maximum(Node* x){
if(x == nil) return x;
while(Rt(x) != nil){
x = Rt(x);
}
return x;
}
Node* Lt_node(Node* x){ //前驱
Node* tmp = x;
if(tmp->GetLt() == nil){
while(tmp->Getpre() != nil && tmp->Getpre()->GetLt() == tmp){
tmp = tmp->Getpre();
}
tmp = tmp->Getpre();
}
else{
tmp = tmp->GetLt();
while(tmp->GetRt() != nil){
tmp = tmp->GetRt();
}
}
return tmp;
}
Node* Rt_node(Node* x){ //后继
Node* tmp = x;
if(tmp->GetRt() == nil){
while(tmp->Getpre() != nil && tmp->Getpre()->GetRt() == tmp){
tmp = tmp->Getpre();
}
tmp = tmp->Getpre();
}
else{
tmp = tmp->GetRt();
while(tmp->GetLt() != nil){
tmp = tmp->GetLt();
}
}
return tmp;
}
public:
Node* root;
Node* nil;
redblacktree(){
nil = new Node({-1,-1},0,BLACK,nil,nil,nil);
root = nil;
}
class iterator{
private:
Node* _node;
public:
Node* Getnode(){ return _node;}
iterator& operator++(){
_node = _node->Rt_node();
return *this;
}
iterator& operator--(){
_node = _node->Lt_node();
return *this;
}
iterator& operator=(iterator a){
_node = a._node;
return *this;
}
friend bool operator ==(iterator a,iterator b){
return a.Getnode() == b.Getnode();
}
friend bool operator !=(iterator a,iterator b){
return a.Getnode() != b.Getnode();
}
pair<T,V>* operator->(){ return _node->Getpair();}
iterator(Node* __node = nullptr):_node(__node){}
iterator(iterator const& iter):_node(iter._node){}
};
Node* find(Node* x,T key){
Node* tmp = x;
while(tmp != nil){
if(tmp->Getdata() > key){
tmp = tmp->GetLt();
}
else if(tmp->Getdata() < key){
tmp = tmp->GetRt();
}
else break;
}
return tmp;
}
Node* Lfind(T key){
Node* parent = nil;
Node* current = root;
Node* t = nil;
while(current != nil){//当当前节点不为空时
if(current->Getdata() > key){
parent = current;
current = current->GetLt();
}
else if(current->Getdata() < key){
parent = current;
current = current->GetRt();
}
else{
t = Lt_node(current);
break;
}
}
if(current->Getdata() == key){
while(t->Getdata() == key){
t = Lt_node(t);
}
return t;
}
if(parent->Getdata() > key){
return Lt_node(parent);
}
else{
return parent;
}
}
Node* Rfind(T key){
Node* parent = nil;
Node* current = root;
Node* t = nil;
while(current != nil){//当当前节点不为空时
if(current->Getdata() > key){
parent = current;
current = current->GetLt();
}
else if(current->Getdata() < key){
parent = current;
current = current->GetRt();
}
else{
t = Rt_node(current);
break;
}
}
if(current->Getdata() == key){
while(t->Getdata() == key){
t = Rt_node(t);
}
return t;
}
if(parent->Getdata() < key){
return Rt_node(parent);
}
else{
return parent;
}
}
void Insert(pair<T,V> p)
{
Node* y = nil;
Node* x = root;
Node* z = new Node(p,1,RED,nil,nil,nil);
while(x != nil){
y = x;
x->Getsize()++;
if(p.first < x->Getdata()) x = Lt(x);
else x = Rt(x);
}
z->Setpre(y);
if(y == nil) root = z;
else if(z->Getdata() < y->Getdata()){
y->SetLt(z);
}
else y->SetRt(z);
z->SetLt(nil);
z->SetRt(nil);
z->Setcolor(RED);
FixAfterInsert(z);
}
void FixAfterInsert(Node* z){
while(color(z->Getpre()) == RED){
if(pre(z) == Lt(pre(pre(z)))){
Node* y = Rt(pre(pre(z)));
if(color(y) == RED){
pre(z)->Setcolor(BLACK); //case1
y->Setcolor(BLACK); //case1
pre(pre(z))->Setcolor(RED); //case1
z = pre(pre(z)); //case1
continue;
}
if(z == Rt(pre(z))){ //case2
z = pre(z); //case2
LRotate(z); //case2
}
pre(z)->Setcolor(BLACK); //case3
pre(pre(z))->Setcolor(RED); //case3
RRotate(pre(pre(z))); //case3
}
else{
Node* y = Lt(pre(pre(z)));
if(color(y) == RED){
pre(z)->Setcolor(BLACK); //case1
y->Setcolor(BLACK); //case1
pre(pre(z))->Setcolor(RED); //case1
z = pre(pre(z)); //case1
continue;
}
if(z == Lt(pre(z))){ //case2
z = pre(z); //case2
RRotate(z); //case2
}
pre(z)->Setcolor(BLACK); //case3
pre(pre(z))->Setcolor(RED); //case3
LRotate(pre(pre(z))); //case3
}
}
root->Setcolor(BLACK);
}
bool Delete(Node* z){
Node* y = z;
int yoc = color(y);
Node* x = z;
if(Lt(z) == nil){
x = Rt(z);
transplant(z,Rt(z));
}
else if(Rt(z) == nil){
x = Lt(z);
transplant(z,Lt(z));
}
else{
y = minimum(Rt(z));
yoc = color(y);
x = Rt(y);
if(pre(y) == z){
x->Setpre(y);
}
else{
transplant(y,Rt(y));
y->SetRt(Rt(z));
Rt(y)->Setpre(y);
}
transplant(z,y);
y->Getsize() = z->Getsize();
y->SetLt(Lt(z));
Lt(y)->Setpre(y);
y->Setcolor(color(z));
}
delete z;
if(yoc == BLACK){
FixAfterDelete(x);
}
return true;
}
bool Delete(T val){
Node* tmp = this->root;
while(tmp != nil){
tmp->Getsize()--;
if(tmp->Getdata() > val){
tmp = tmp->GetLt();
}
else if(tmp->Getdata() < val){
tmp = tmp->GetRt();
}
else break;
}
if(tmp == nil){
return false;
}
else{
return Delete(tmp);
}
}
void FixAfterDelete(Node* x){
while(x != root && color(x) == BLACK){
if(Lt(pre(x)) == x){
Node* w = Rt(pre(x));
if(color(w) == RED){
w->Setcolor(BLACK); //case1
pre(x)->Setcolor(RED); //case1
LRotate(pre(x)); //case1
w = Rt(pre(x)); //case1
}
if(color(Lt(w)) == BLACK && color(Rt(w)) == BLACK){
w->Setcolor(RED); //case2
x = pre(x); //case2
}
else{
if(color(Rt(w)) == BLACK){
Lt(w)->Setcolor(BLACK); //case3
w->Setcolor(RED); //case3
RRotate(w); //case3
w = Rt(pre(x)); //case3
}
w->Setcolor(color(pre(x))); //case4
pre(x)->Setcolor(BLACK); //case4
Rt(w)->Setcolor(BLACK); //case4
LRotate(pre(x)); //case4
x = root; //case4
}
}
else{
Node* w = Lt(pre(x));
if(color(w) == RED){
w->Setcolor(BLACK); //case1
pre(x)->Setcolor(RED); //case1
RRotate(pre(x)); //case1
w = Lt(pre(x)); //case1
}
if(color(Lt(w)) == BLACK && color(Rt(w)) == BLACK){
w->Setcolor(RED); //case2
x = pre(x); //case2
}
else{
if(color(Lt(w)) == BLACK){
Rt(w)->Setcolor(BLACK); //case3
w->Setcolor(RED); //case3
LRotate(w); //case3
w = Lt(pre(x)); //case3
}
w->Setcolor(color(pre(x))); //case4
pre(x)->Setcolor(BLACK); //case4
Lt(w)->Setcolor(BLACK); //case4
RRotate(pre(x)); //case4
x = root; //case4
}
}
}
x->Setcolor(BLACK);
}
Node* findkth(int k,Node* p){
if(p->GetLt() == nil){
if(k == 1){
return p;
}
else{
return findkth(k-1,p->GetRt());
}
}
else{
if(p->GetLt()->Getsize() == k-1) return p;
else if(p->GetLt()->Getsize() >= k) return findkth(k,p->GetLt());
else return findkth(k-p->GetLt()->Getsize()-1,p->GetRt());
}
}
int find_rank(T v,Node* p){
if(p == nil) return 1;
else if(p->Getdata() >= v) return find_rank(v,p->GetLt());
else return (1 + (p->GetLt() ? p->GetLt()->Getsize() : 0 ) + find_rank(v,p->GetRt()));
}
Node* begin(){
Node* t = root;
while(t->Lt_node() != nil){
t = t->Lt_node();
}
return t;
}
Node* end(){
Node* t = root;
while(t->Rt_node() != nil){
t = t->Rt_node();
}
return t;
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
redblacktree<int,int>* mp = new redblacktree<int,int>();
int n,m,num;
cin >> n;
for(int i = 0;i < n; i++){
cin >> m >> num;
if(m == 1){
mp->Insert({num,1});
}
else if(m == 2){
mp->Delete(num);
}
else if(m == 3){
cout << mp->find_rank(num,mp->root) << "\n";
}
else if(m == 4){
cout << mp->findkth(num,mp->root)->Getdata() << "\n";
}
else if(m == 5){
cout << mp->Lfind(num)->Getdata() << "\n";
}
else if(m == 6){
cout << mp->Rfind(num)->Getdata() << "\n";
}
}
return 0;
}treap版本的
在二叉搜索树中,在某些情况下有可能会让二叉搜索树退化成一条链,为了解决这样的问题,在树的结点里加一个修正值,由树的结点的val和fix共同决定树的结构。fix值是随机的。
treap就是tree + heap,其中key值满足二叉搜索树的性质,fix值满足堆的性质。
插入结点操作:先从根节点开始,一步步寻找插入位置,一旦发现空结点就插入,插入之后,判断当前的结点的fix值是否满足堆的性质,如果不满足就进行旋转调整,旋转时并不破坏树的二叉搜索树的性质,旋转之后有可能上一层的结点的fix值的堆性质被破坏,所以要一步步向上判断。
删除结点操作:先寻找删除结点的位置,找到后如果该结点没有叶结点就直接删除,如果该结点有一个叶结点就用叶结点去替代。如果有两个叶结点就进行适当的旋转,直到该结点有一个叶结点或没有叶结点。
完整代码:指针实现版本
#include <bits/stdc++.h>
using namespace std;
class Treap{
private:
class Node{
private:
Node* Lt;
Node* Rt;
int val;
int fix;
int size;
public:
Node(int val,int fix):Lt(nullptr),Rt(nullptr),val(val),fix(fix),size(1){}
Node*& GetLt(){ return Lt;}
Node*& GetRt(){ return Rt;}
void SetLt(Node* t){ Lt = t;}
void SetRt(Node* t){ Rt = t;}
int Getval(){ return val;}
int Getfix(){ return fix;}
int& Getsize(){ return size;}
};
Node*& Lt(Node* node){
return node->GetLt();
}
Node*& Rt(Node* node){
return node->GetRt();
}
int Getsize(Node*& p){
if(p == nullptr) return 0;
else return p->Getsize();
}
void update(Node*& p){
p->Getsize() = Getsize(p->GetLt()) + Getsize(p->GetRt()) + 1;
}
void LRotate(Node*& p){
Node* tmp = p->GetRt();
p->SetRt(tmp->GetLt());
tmp->SetLt(p);
update(p);
p = tmp;
update(p);
}
void RRotate(Node*& p){
Node* tmp = p->GetLt();
p->SetLt(tmp->GetRt());
tmp->SetRt(p);
update(p);
p = tmp;
update(p);
}
public:
Treap():root(nullptr){}
Node* root;
void Insert(Node*& p,int num){
if(p == nullptr){
p = new Node(num,rand());
return;
}
if(num < p->Getval()){
Insert(p->GetLt(),num);
update(p);
if(p->GetLt()->Getfix() < p->Getfix()) RRotate(p);
}
else{
Insert(p->GetRt(),num);
update(p);
if(p->GetRt()->Getfix() < p->Getfix()) LRotate(p);
}
}
void Delete(Node*& p,int num){
if(p == nullptr) return;
if(p->Getval() == num){
if(p->GetLt() != nullptr && p->GetRt() != nullptr){
if(p->GetLt()->Getfix() < p->GetRt()->Getfix()){
RRotate(p);
Delete(p->GetRt(),num);
}
else{
LRotate(p);
Delete(p->GetLt(),num);
}
update(p);
}
else{
if(p->GetLt() == nullptr && p->GetRt() == nullptr){
p = nullptr;
}
else{
if(p->GetLt()) p = p->GetLt();
else p = p->GetRt();
}
}
}
else{
if(num < p->Getval()) Delete(p->GetLt(),num);
else Delete(p->GetRt(),num);
update(p);
}
}
int GetRank(Node *&p,int num)//找到x的排名,=找有多少个元素小于x
{
if(p == nullptr) return 0;//空节点不计数
if(p->Getval() >= num) return GetRank(p->GetLt(), num);//去左子树算排名
int Lsize = 0;
if(p->GetLt() != nullptr) Lsize = p->GetLt()->Getsize();
return Lsize + GetRank(p->GetRt(), num) + 1;//返回排名
}
int Getkth(Node *&p,int k)//找排名为k的元素
{
int Lsize = 0 ;
if(p->GetLt()) Lsize = p->GetLt()->Getsize();//左子树大小
if(k == Lsize + 1) return p->Getval();//找到返回
if(k <= Lsize ) return Getkth(p->GetLt(),k);//是其左子树的第k名
else return Getkth(p->GetRt(),k-Lsize-1);//是其右子树的k-lsize-1名
}
int Getpre(Node* p,int num){
if(p == nullptr) return 0;
if(p->Getval() >= num) return Getpre(p->GetLt(),num);
int tmp = Getpre(p->GetRt(),num);
if(tmp != 0) return tmp;
else return p->Getval();
}
int Getsuc(Node* p,int num){
if(p == nullptr) return 0;
if(p->Getval() <= num) return Getsuc(p->GetRt(),num);
int tmp = Getsuc(p->GetLt(),num);
if(tmp != 0) return tmp;
else return p->Getval();
}
};
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
Treap* t = new Treap;
int n,m,opt;
cin >> n;
for(int i = 0;i < n; i++){
cin >> m >> opt;
if(m == 1){
t->Insert(t->root,opt);
}
else if(m == 2){
t->Delete(t->root,opt);
}
else if(m == 3){
cout << t->GetRank(t->root,opt)+1 << '\n';
}
else if(m == 4){
cout << t->Getkth(t->root,opt) << '\n';
}
else if(m == 5){
cout << t->Getpre(t->root,opt) << '\n';
}
else if(m == 6){
cout << t->Getsuc(t->root,opt) << '\n';
}
}
return 0;
}