[数据结构与算法]《算法系列》之 数组

简介

??一般纯数组的题都不会太难，但数组作为基本数据结构，经常和其它算法类型同时使用，比如用数组实现其它数据结构，双指针，滑动窗口，贪心，动态规划等。其中可用数组实现哈希表，可以提高效率，减少空间浪费，之后的内容会和大家分享。纯数组题有一种题比较难，就是模拟题，模拟题目实现的过程，这种题不需要很强的逻辑，但很考代码掌握能力。

理论基础

??数组（array）是一种复合数据类型，它是有序数据的集合，在存储空间中也是按顺序存储。数组中的每个元素具有相同的数据类型，可以用一个统一的数组名和不同的下标来确定数组中唯一的元素。根据数组的维度，可以将其分为一维数组、二维数组和多维数组等。

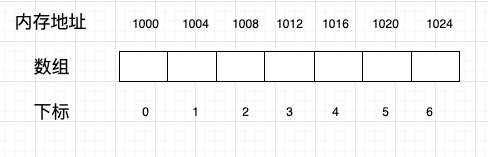
数组具有以下特点：

• 在存储空间中按顺序存储，地址连续。
• 数值数组元素的默认值为 0，而引用元素的默认值为 null。
• 数组的索引从 0 开始，如果数组有 n 个元素，那么数组的索引是从 0 到（n-1）。
• 数组元素可以是任何类型，包括数组类型。
• 数组的元素是不能删的，只能覆盖，平时删除操作也是依次用后一位覆盖，因为申请且初始化后，存储空间就固定了。

// Java中数组申请方式

数据类型[ ] 数组名；
或 
数据类型 数组名[ ]；

String[] names;
int [] age;
double height[];

解题心得

• 数组是非常基础的数据结构，如果只是单独的数组题，一般不会太难。
• 数组题常与其它类型的题同时出现，这时我们按其它类型处理。
• 数组题里，摸拟题可能是最难的了，这种题一般思维要求不高，但代码掌握能力要求极高，需要多加练习。
• 数组特殊情况下可以做哈希表。
• 数组元素是不能删除的，只能覆盖。
• 二分法解题方式常出现在数组题里，写二分法时要注意是左开右闭，还是右开左闭，和注意边界值等。

算法题目

4. 寻找两个正序数组的中位数

题目解析：由于算法复杂度要求为 O(log (m+n))，所以不能先归并再找中位数。我们一看复杂度就知道，大概率是用类二分法，才会是O(log (m+n))的复杂度，这道题可以理解成寻找两个有序数组中的第k小的数。
代码如下：

/**
 * 二分法查找
 */
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length1 = nums1.length, length2 = nums2.length;
        int totalLength = length1 + length2;
        if (totalLength % 2 == 1) {
            int midIndex = totalLength / 2;
            double median = getKthElement(nums1, nums2, midIndex + 1);
            return median;
        } else {
            int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;
            double median = (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;
            return median;
        }
    }

    public int getKthElement(int[] nums1, int[] nums2, int k) {

        int length1 = nums1.length, length2 = nums2.length;
        int index1 = 0, index2 = 0;
        int kthElement = 0;

        while (true) {
            // 边界情况
            if (index1 == length1) {
                return nums2[index2 + k - 1];
            }
            if (index2 == length2) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {
                return Math.min(nums1[index1], nums2[index2]);
            }
            
            // 正常情况
            int half = k / 2;
            int newIndex1 = Math.min(index1 + half, length1) - 1;
            int newIndex2 = Math.min(index2 + half, length2) - 1;
            int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];
            if (pivot1 <= pivot2) {
                k -= (newIndex1 - index1 + 1);
                index1 = newIndex1 + 1;
            } else {
                k -= (newIndex2 - index2 + 1);
                index2 = newIndex2 + 1;
            }
        }
    }
}

33. 搜索旋转排序数组

题目解析：将旋转过后的数组，依然使用二分法查找。从中分开后，一半为有序，另一半为有序或杂序，再分(递归)。
代码如下：

/**
 * 二分法查找
 */
class Solution {
    public int search(int[] nums, int target) {

        if (nums[0] == target) {
            return 0;
        }

        int left = 0;
        int right = nums.length - 1;
        int middle = (left + right) / 2;
        while (left != right) {
            if (target == nums[left]) {
                return left;
            }
            if (target == nums[right]) {
                return right;
            }
            if (nums[left] < nums[middle]) {
                if (nums[left] <= target && target <= nums[middle]) {
                    if (target == nums[middle]) {
                        return middle;
                    }
                    right = middle;
                    middle = (left + right) / 2;
                } else {
                    left = middle;
                    middle = (left + right) / 2;
                }
            } else {
                if (target >= nums[left] || target <= nums[middle]) {
                    if (target == nums[middle]) {
                        return middle;
                    }
                    right = middle;
                    middle = (left + right) / 2;
                } else {
                    left = middle;
                    middle = (left + right) / 2;
                }
            }
        }
        return -1;
    }
}

34. 在排序数组中查找元素的第一个和最后一个位置

题目解析：直接用两次二分法，分别求出target的start和end位置，写二分法时，需要注意是左闭右开，还是右闭左开，二分法的书写还是需要注意，要不然很容易变成：“脑袋会了，手不会”。
代码如下：

/**
 * 用两次二分法，分别求出 start 和 end 位置
 */
class Solution {
    public int[] searchRange(int[] nums, int target) {
        int start = 0;
        int end = nums.length - 1;
        int[] ans = {-1, -1};
        if (nums.length == 0) {
            return ans;
        }
        while (start <= end) {
            int mid = (start + end) / 2;
            if (target == nums[mid]) {
                int n = mid > 0 ? nums[mid - 1] : Integer.MIN_VALUE;
                if (target > n || mid == 0) {
                    ans[0] = mid;
                    break;
                }
                end = mid - 1;
            } else if (target < nums[mid]) {
                end = mid - 1;
            } else {
                start = mid + 1;
            }
        }
        start = 0;
        end = nums.length - 1;
        while (start <= end) {
            int mid = (start + end) / 2;
            if (target == nums[mid]) {
                int n = mid < nums.length - 1 ? nums[mid + 1] : Integer.MAX_VALUE;
                if (target < n || mid == nums.length - 1) {
                    ans[1] = mid;
                    break;
                }
                start = mid + 1;
            } else if (target < nums[mid]) {
                end = mid - 1;
            } else {
                start = mid + 1;
            }
        }
        return ans;
    }
}

35. 搜索插入位置

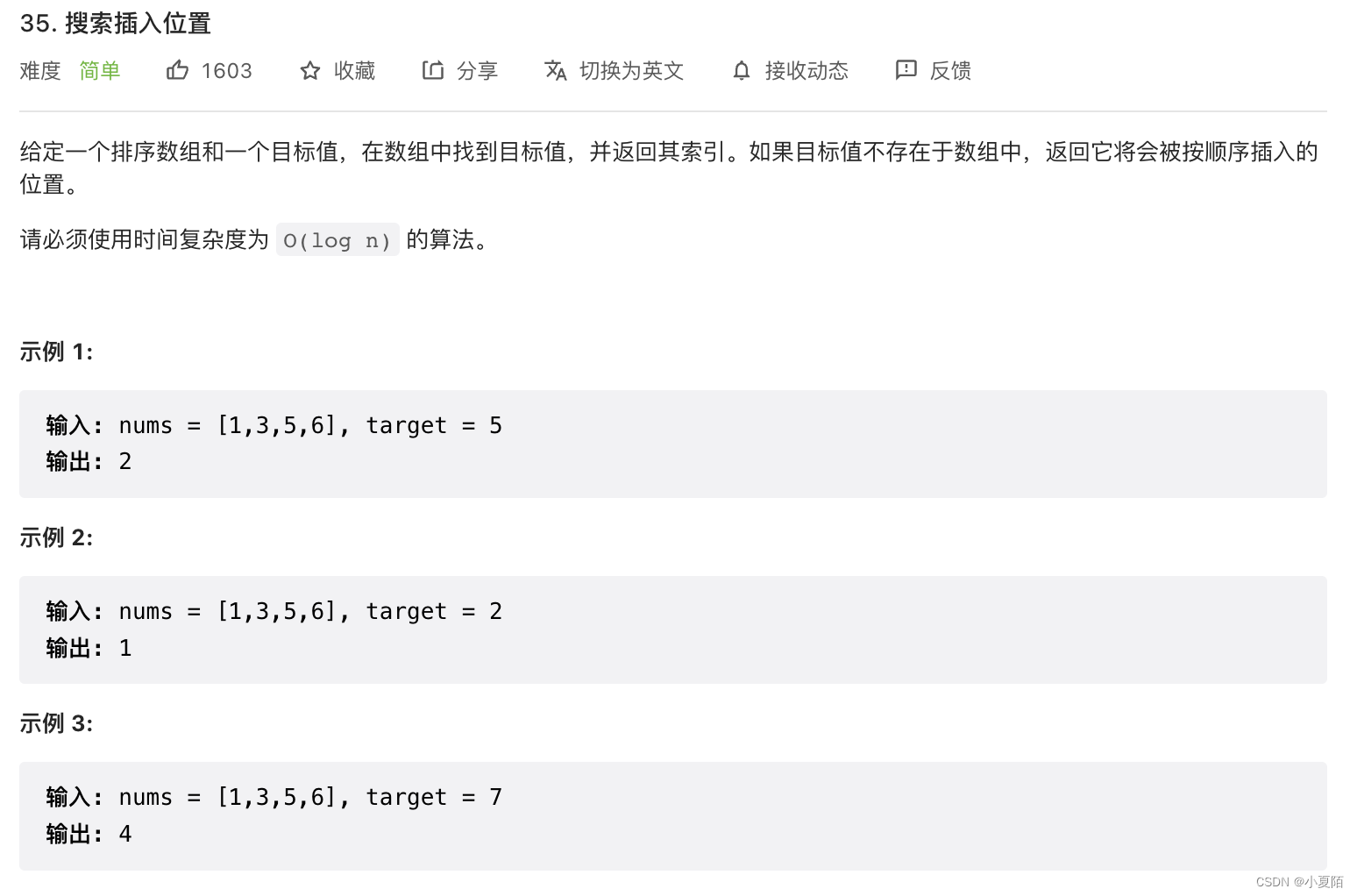
题目解析：这种题，一看时间复杂度是O(log n)，则我们就应该知道要用二分法，同样需要注意是左闭右开，还是右闭左开，和一些边界值的确定，不能模模糊糊的就AC了。
代码如下：

/**
 * 二分法查找
 */
class Solution {
    public int searchInsert(int[] nums, int target) {

        if (nums.length == 0) {
            return 0;
        }

        int start = 0;
        int end = nums.length;
        while (start < end) {
            int middle = (start + end) / 2;
            if (target == nums[middle]) {
                return middle;
            } else if (target < nums[middle]) {
                end = middle;
            } else {
                start = middle + 1;
            }
        }
        return start;
    }
}

36. 有效的数独

题目解析：数字在行，列，小棋盘内，分别没有重复，即为有效数独。这里可以用HashSet存储，而后判断，如有重复，直接返回false即可。
代码如下：

/**
 * 数组
 */
class Solution {
    public boolean isValidSudoku(char[][] board) {
        // 记录某行，某位数字是否已经被摆放
        boolean[][] row = new boolean[9][9];
        // 记录某列，某位数字是否已经被摆放
        boolean[][] col = new boolean[9][9];
        // 记录某 3x3 宫格内，某位数字是否已经被摆放
        boolean[][] block = new boolean[9][9];

        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] != '.') {
                    int num = board[i][j] - '1';
                    int blockIndex = i / 3 * 3 + j / 3;
                    if (row[i][num] || col[j][num] || block[blockIndex][num]) {
                        return false;
                    } else {
                        row[i][num] = true;
                        col[j][num] = true;
                        block[blockIndex][num] = true;
                    }
                }
            }
        }
        return true;
    }
}

41. 缺失的第一个正数

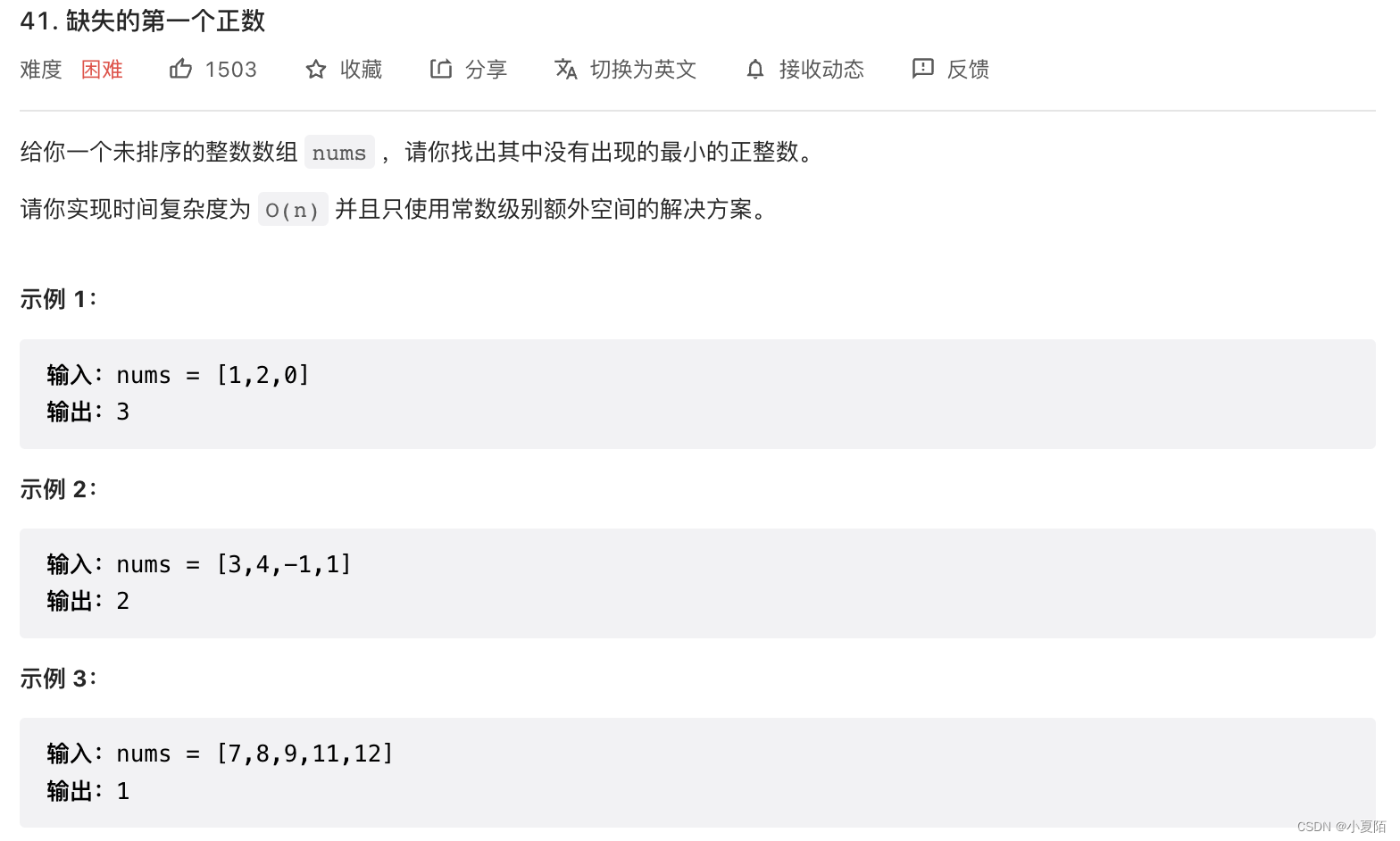
题目解析：按格式置换后，数组应当有[1, 2, …, N]的形式，但其中有若干个位置上的数是错误的，每一个错误的位置就代表了一个缺失的正数。
代码如下：

/**
 * 置换
 */
class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; ++i) {
            while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
                int temp = nums[nums[i] - 1];
                nums[nums[i] - 1] = nums[i];
                nums[i] = temp;
            }
        }
        for (int i = 0; i < n; ++i) {
            if (nums[i] != i + 1) {
                return i + 1;
            }
        }
        return n + 1;
    }
}

48. 旋转图像

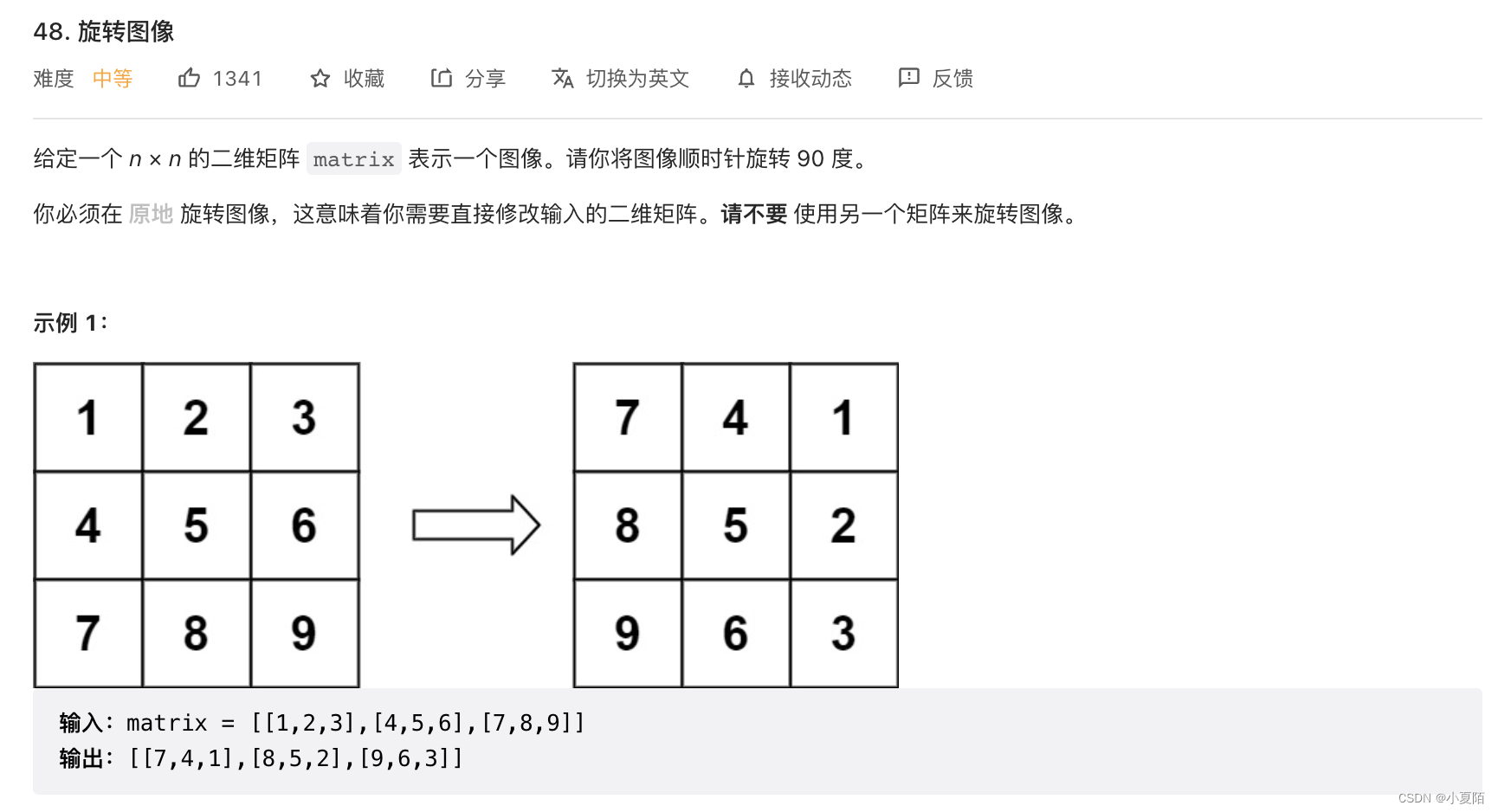
题目解析：先转置，再左右镜像对换。因为转置和镜像对换时，只需要两个位置对调。
代码如下：

/**
 * 数组
 */
class Solution {
    public void rotate(int[][] matrix) {
        // 转置（斜对称）
        int n = matrix.length;
        for (int i = 0; i < n; i++) {
            for (int j = i; j < n; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        // 镜像对换
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n / 2; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[i][n - j - 1];
                matrix[i][n - j - 1] = temp;
            }
        }
    }
}

57. 插入区间

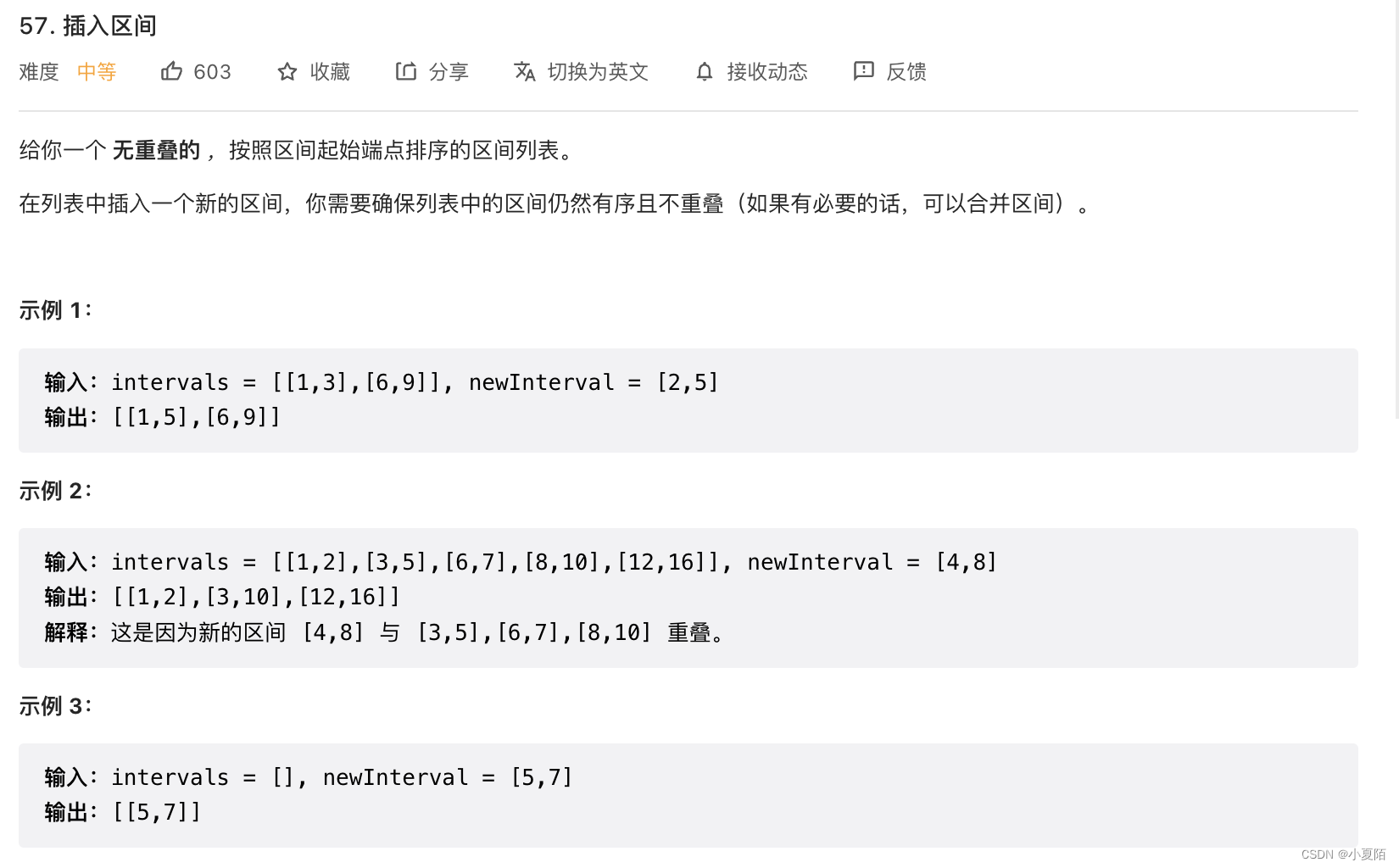
题目解析：分成左边界和右边界的数组，分开处理。
代码如下：

/**
 * 数组
 */
class Solution {
    public int[][] insert(int[][] intervals, int[] newInterval) {
        int left = newInterval[0];
        int right = newInterval[1];

        boolean isFisrt = true;
        List<int[]> res = new ArrayList<>();
        // 在插入区间的右侧且无交集
        for (int[] interval : intervals) {
            if (interval[0] > right) {
                if (isFisrt) {
                    res.add(new int[]{left, right});
                    isFisrt = false;
                }
                res.add(interval);
                // 在插入区间的左侧且无交集
            } else if (interval[1] < left) {
                res.add(interval);
                // 其它为有交集的情况，分别确定左右边界
            } else {
                left = Math.min(left, interval[0]);
                right = Math.max(right, interval[1]);
            }
        }
        // 如果原区间为空，则直接添加新区间
        if (isFisrt) {
            res.add(new int[]{left, right});
        }
        return res.toArray(new int[res.size()][]);
    }
}

73. 矩阵置零

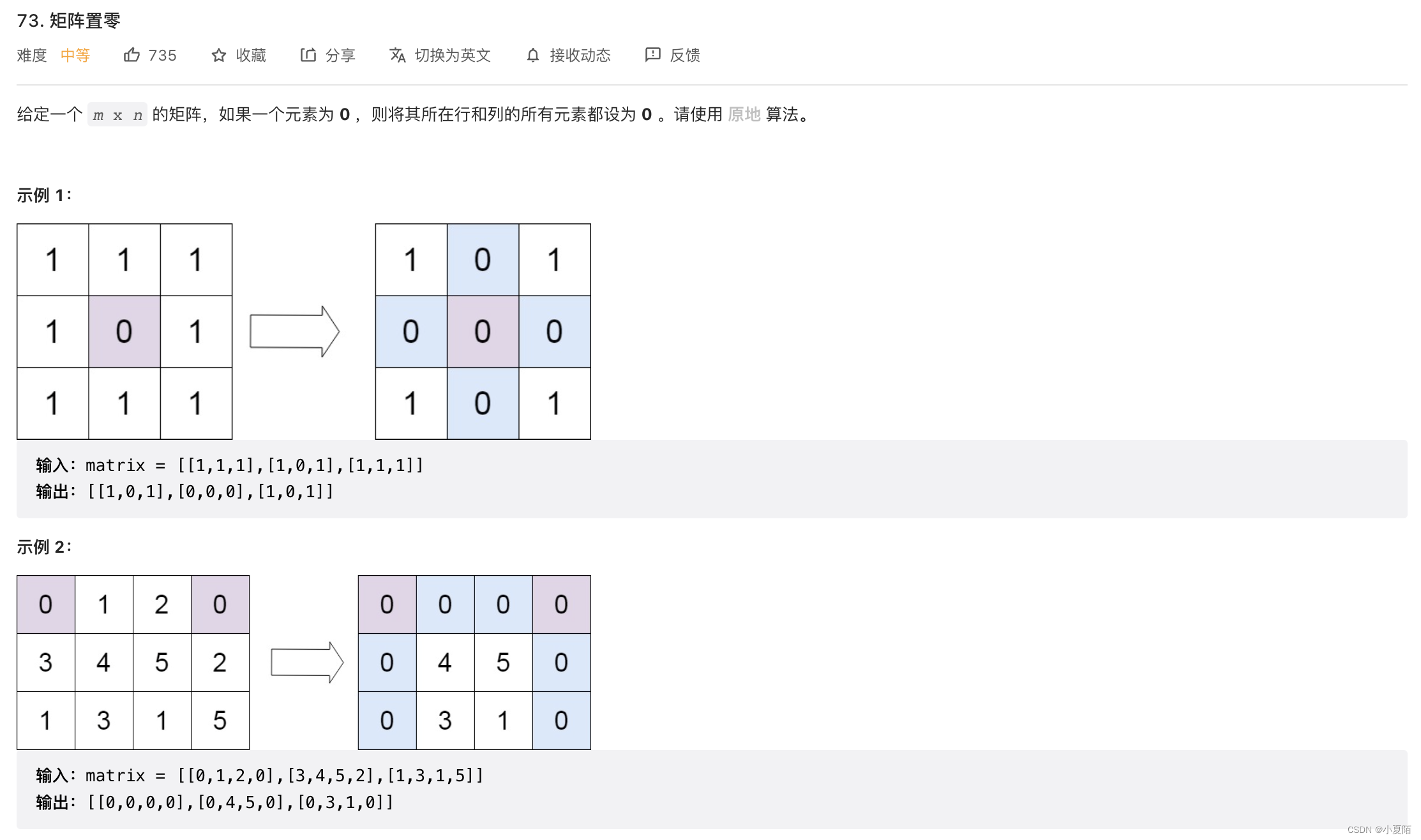
题目解析：用两个布尔变量解决。利用数组的首行和首列来记录 0 值。从数组下标的 A[1][1] 开始遍历，两个布尔值记录首行首列是否需要置0。
代码如下：

/**
 * 数组
 */
class Solution {
    public void setZeroes(int[][] matrix) {
        boolean rowFlag = false;
        //判断首行
        for (int i = 0; i < matrix[0].length; i++) {
            if (matrix[0][i] == 0) {
                rowFlag = true;
                break;
            }
        }

        boolean colFlag = false;
        for (int i = 0; i < matrix.length; i++) {
            if (matrix[i][0] == 0) {
                colFlag = true;
                break;
            }
        }

        for (int i = 1; i < matrix.length; i++) {
            for (int j = 1; j < matrix[0].length; j++) {
                if (matrix[i][j] == 0){
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }

        for (int i = 1; i < matrix[0].length; i++) {
            if (matrix[0][i] == 0) {
                for (int j = 0; j < matrix.length; j++) {
                    matrix[j][i] = 0;
                }
            }
        }

        for (int i = 1; i < matrix.length; i++) {
            if (matrix[i][0] == 0) {
                for (int j = 0; j < matrix[0].length; j++) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (rowFlag){
            for (int i = 0; i < matrix[0].length; i++) {
                matrix[0][i] = 0;
            }
        }
        if (colFlag){
            for (int i = 0; i < matrix.length; i++) {
                matrix[i][0] = 0;
            }
        }
    }
}

74. 搜索二维矩阵

题目解析：二分法查找，把二维数组看做一维数组即可。取mid值时，用整除和取模确定mid值即可。
代码如下：

/**
 * 数组
 */
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        int begin, mid, end;
        begin = mid = 0;
        int len1 = matrix.length, len2 = matrix[0].length;
        end = len1 * len2 - 1;
        while (begin < end) {
            mid = (begin + end) / 2;
            // 取中间位置数为mid: row = mid / len2, cloum = mid % len2
            if (matrix[mid / len2][mid % len2] < target) {
                begin = mid + 1;
            } else {
                end = mid;
            }
        }
        // 最后判断 mid 和目标值是否相等
        return matrix[begin / len2][begin % len2] == target;
    }
}

81. 搜索旋转排序数组 II

题目解析：二分法查找，因为有重复数字加旋转，直接二分法不可行。故，需要先找到旋转点，如果过程中找到目标值，直接返回true，没找到，但找到旋转点后，再对后半段用二分法。
代码如下：

/**
 * 数组
 */
class Solution {
    public boolean search(int[] nums, int target) {

        if (nums.length == 1) return nums[0] == target;

        int sit = nums.length - 1;
        // 找到旋转点
        while (sit >= 1) {
            if (nums[sit - 1] == target || nums[sit] == target) {
                return true;
            }
            if (nums[sit - 1] <= nums[sit]) sit--;
            else break;
        }
        if (sit != 0) sit--;

        int min = 0;
        int max = nums.length - 1;
        if (nums[0] <= target && target <= nums[sit]) max = sit;
        else min = sit + 1;

        // 二分查找
        while (min <= max) {
            int mid = min + ((max - min) >> 1);
            if (nums[mid] > target) max = mid - 1;
            else if (nums[mid] < target) min = mid + 1;
            else return true;
        }
        return false;
    }
}

130. 被围绕的区域

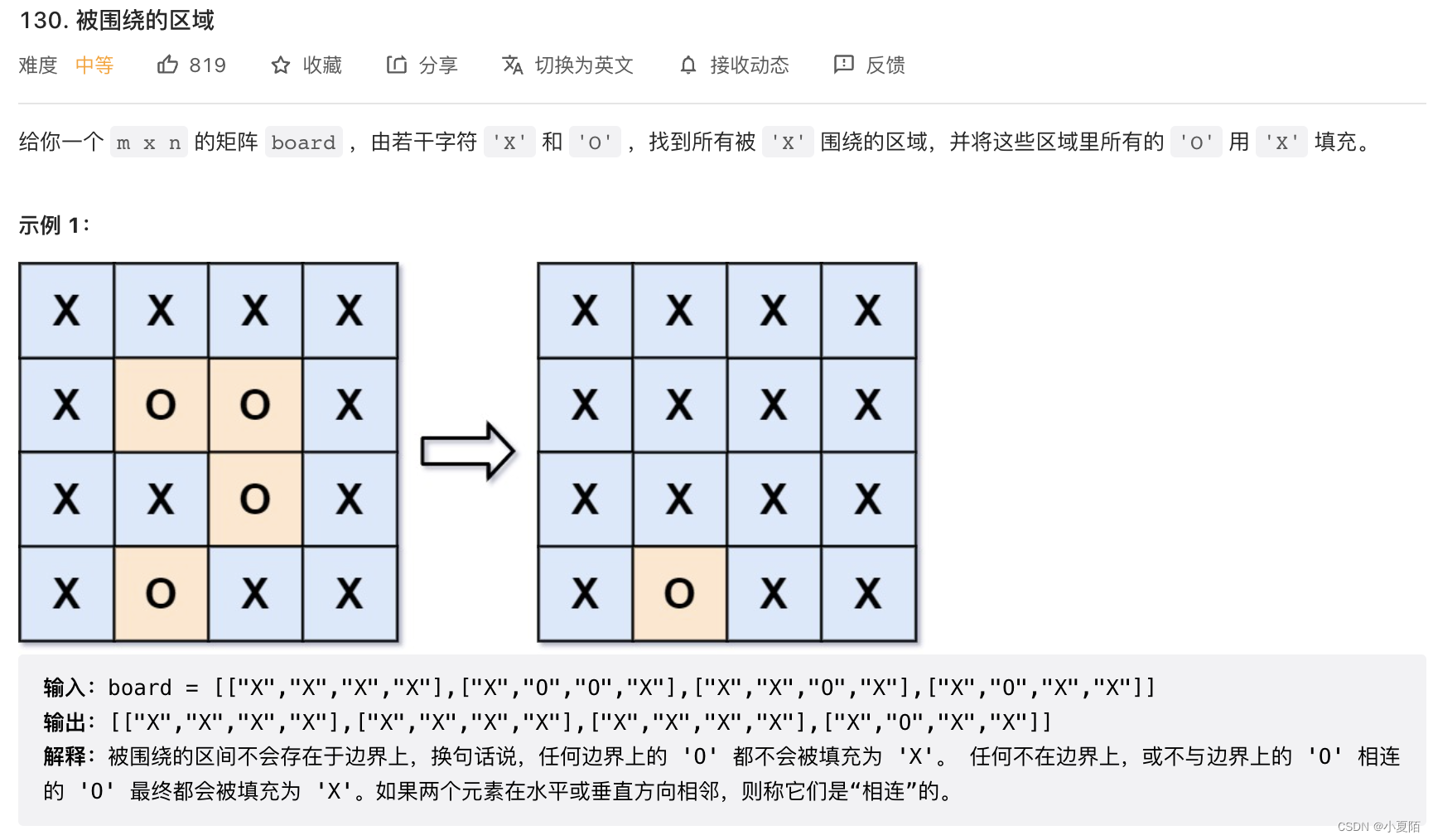
题目解析：找出各边界的O然后用A代替，深搜其节点，用A代替连接的各个节点。最后把其它O换成X，把A替换成O。
代码如下：

/**
 * 深度优先搜索 
 */
class Solution {
    int n, m;

    public void solve(char[][] board) {
        n = board.length;
        if (n == 0) {
            return;
        }
        m = board[0].length;
        for (int i = 0; i < n; i++) {
            dfs(board, i, 0);
            dfs(board, i, m - 1);
        }
        for (int i = 1; i < m - 1; i++) {
            dfs(board, 0, i);
            dfs(board, n - 1, i);
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }
    }

    public void dfs(char[][] board, int x, int y) {
        if (x < 0 || x >= n || y < 0 || y >= m || board[x][y] != 'O') {
            return;
        }
        board[x][y] = 'A';
        dfs(board, x + 1, y);
        dfs(board, x - 1, y);
        dfs(board, x, y + 1);
        dfs(board, x, y - 1);
    }
}

152. 乘积最大子数组

题目解析：分别求出以i为右边界的最大值，找到最大者即可。
代码如下：

/**
 * 数组
 */
class Solution {
    public int maxProduct(int[] nums) {
        // 结果值
        int res = nums[0];
        // 以第i个数为右边界的最大值
        int maxV = nums[0];
        // 以第i个数为右边界的最小值
        int minV = nums[0];
        int len = nums.length;
        for (int i = 1; i < len; i++) {
            if (nums[i] > 0) {
                maxV = Math.max(nums[i], nums[i] * maxV);
                minV = Math.min(nums[i], nums[i] * minV);
            } else if (nums[i] == 0) {
                maxV = 0;
                minV = 0;
            } else {
                int temp = Math.max(nums[i], nums[i] * minV);
                minV = Math.min(nums[i], nums[i] * maxV);
                maxV = temp;
            }
            res = Math.max(res, maxV);
        }
        return res;
    }
}

153. 寻找旋转排序数组中的最小值

题目解析：把该数组分成两段，如果左右两段都是升序的，则说明，整段数组都是升序的，直接返回最左边数。如果一段是升序，另一段非升序，则说明，最小数一定在非升序段，接着使用二法查找。
代码如下：

/**
 * 二分法查找
 */
class Solution {
    public int findMin(int[] nums) {
        if (nums.length <= 1) {
            return nums[0];
        }
        int left = 0;
        int right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            // 如果整个数组都是升序，直接返回最小数
            if (nums[left] <= nums[mid] && nums[mid] <= nums[right]) {
                return nums[left];
            } else if (nums[left] <= nums[mid]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return 0;
    }
}

154. 寻找旋转排序数组中的最小值 II

题目解析：把该数组分成两段，如果左右两段都是升序的，则说明，整段数组都是升序的，直接返回最左边数。如果一段是升序，另一段非升序，则说明，最小数一定在非升序段，接着使用二法查找。如果left，mid，right全相等则只将 right-1，逐渐缩小范围，防止左中右都为重复数，最小数藏在其中的情况。
代码如下：

/**
 * 二分法查找
 */
class Solution {
    public int findMin(int[] nums) {
        if (nums.length <= 1) {
            return nums[0];
        }
        int left = 0;
        int right = nums.length - 1;
        int mid = left + (right - left) / 2;
        while (left <= right) {
            mid = left + (right - left) / 2;
            // 如果整个数组都是升序，直接返回最小数
            if (nums[left] < nums[mid] && nums[mid] < nums[right]) {
                return nums[left];
            } else if (nums[mid] > nums[right]) {
                left = mid + 1;
            } else if (nums[mid] < nums[right]) {
                right = mid;
                // 等于即有重复的情况，将右边界减一，逐渐缩小范围
            } else {
                right--;
            }
        }
        return nums[left];
    }
}

162. 寻找峰值

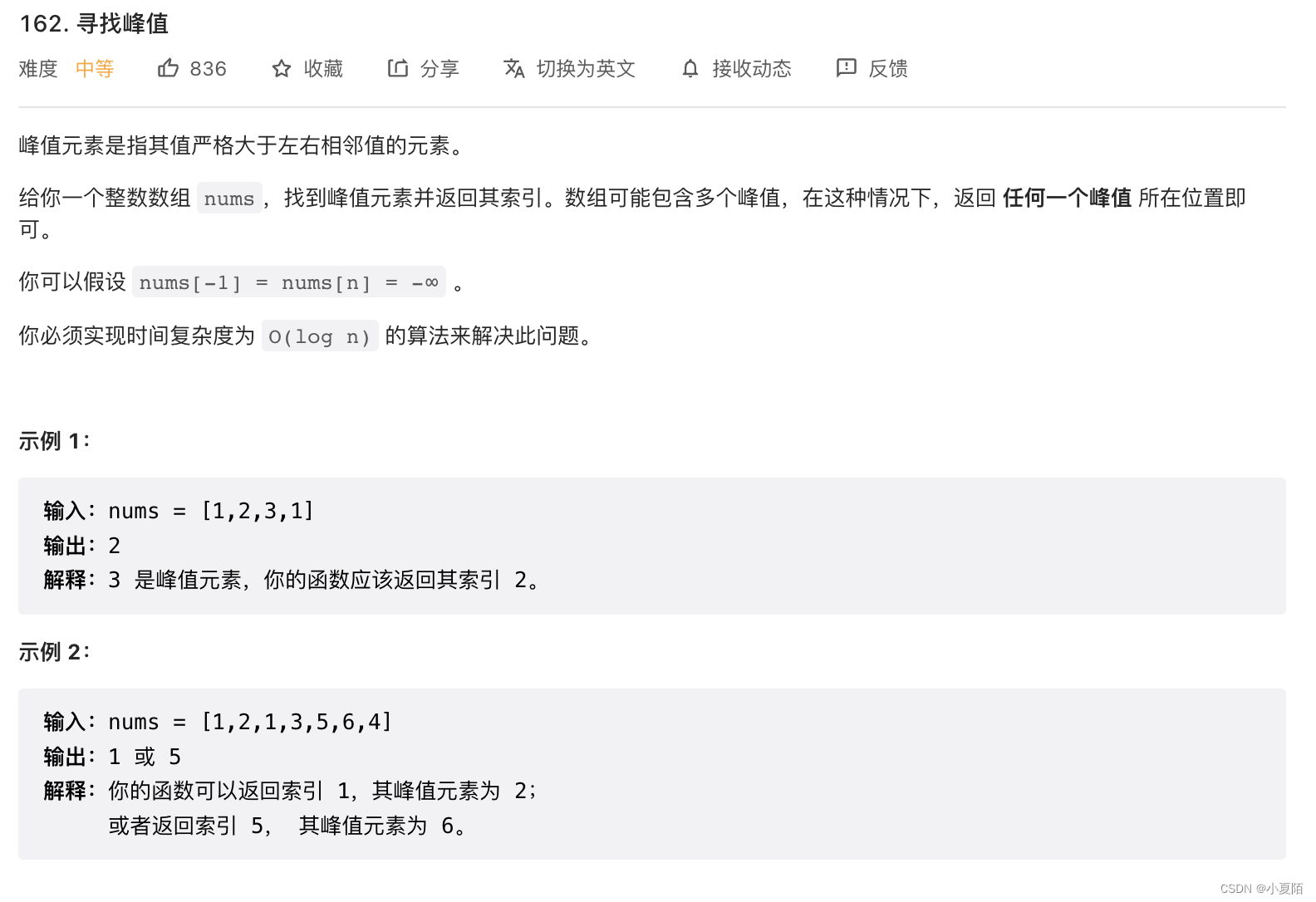
题目解析：数组可看做二维坐标中突起的曲线，要做的是，把峰值留在中间，由两边向中间缩。
代码如下：

/**
 * 二分法
 */
class Solution {
    public int findPeakElement(int[] nums) {
        int l = 0;
        int r = nums.length - 1;

        // 二分法 [l, r] 永远表示查询之后仍然可能的范围
        while (l < r) {
            int mid = (l + r) / 2;

            // nums[-1] = nums[n] = -∞
            if (nums[mid] < nums[mid+1]) {
                // 如果 mid + 1 更大， 说明 mid 之后肯定还在爬升，mid+1 之后有峰
                l = mid + 1;
            } else {
                // 如果 mid 更大， 说明 mid 之前有峰
                r = mid;
            }
        }

        // 条件退出的时候 l 和 r 相等， 而我们始终保持 [l, r] 内有峰。 所以，r就是峰所在的位置。
        return r;
    }
}

169. 多数元素

题目解析：题目要求空间复杂度O(1)，也可用排序，而后数组中间的值一定是众数值，Boyer-Moore 投票算法，因为众数超过一半以上，比其它数加起来的票都多，所以一定会留在场上，笑到最后。
代码如下：

/**
 * 数组
 */
class Solution {
    public int majorityElement(int[] nums) {
        int count = 0;
        Integer candidate = null;

        for (int num : nums) {
            if (count == 0) {
                candidate = num;
            }
            count += (num == candidate) ? 1 : -1;
        }

        return candidate;
    }
}

200. 岛屿数量

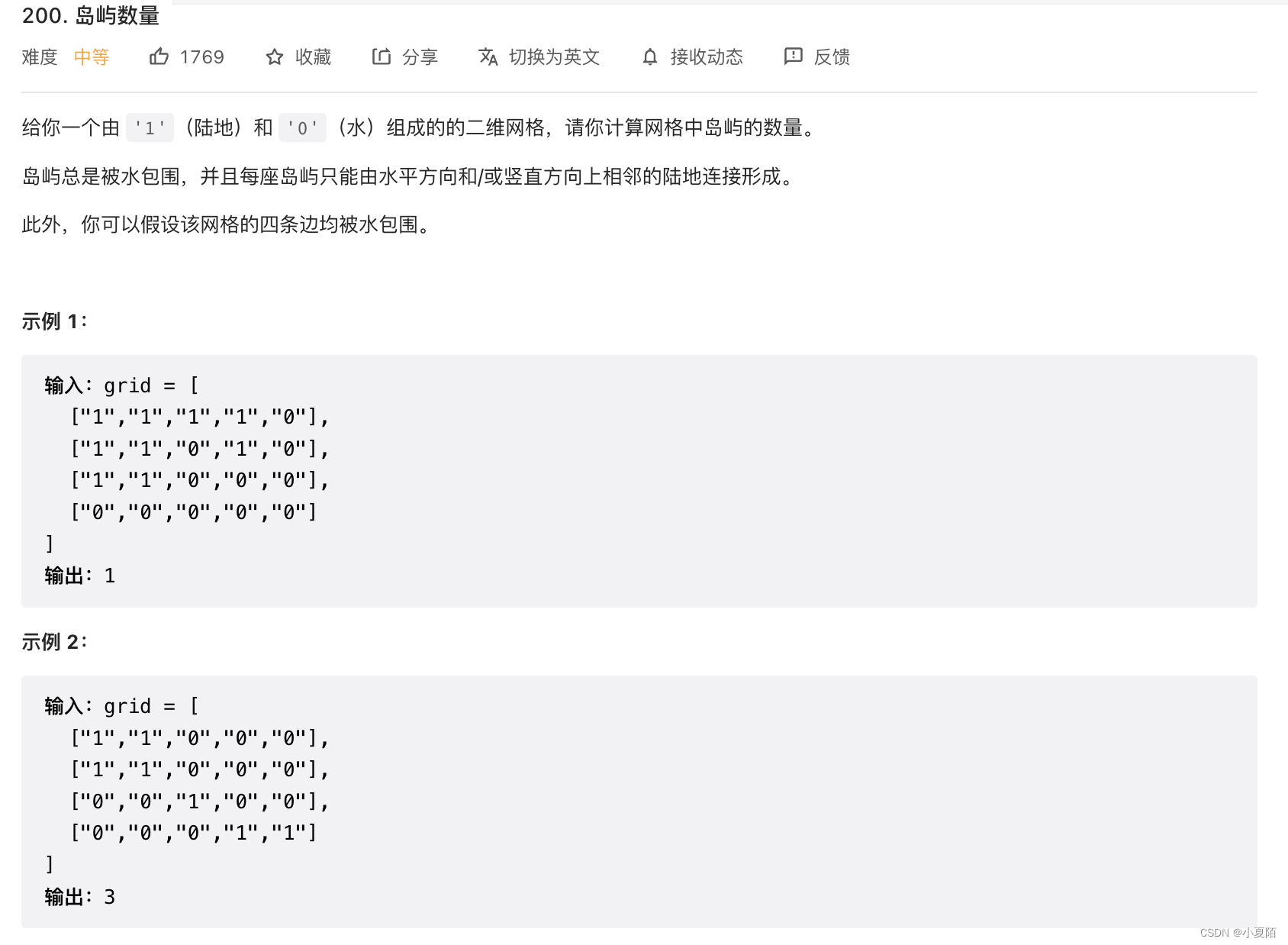
题目解析：遍历矩阵，当当前值为1时，把周围上下左右的1全部“感染”为2，然后岛屿数加1，最后返回小岛数量即可。
代码如下：

/**
 * 矩阵 
 */
class Solution {
    public int numIslands(char[][] grid) {
        int islandNum = 0;
        for(int i = 0; i < grid.length; i++){
            for(int j = 0; j < grid[0].length; j++){
                if(grid[i][j] == '1'){
                    infect(grid, i, j);
                    islandNum++;
                }
            }
        }
        return islandNum;
    }
    // 感染函数
    public void infect(char[][] grid, int i, int j){
        if(i < 0 || i >= grid.length ||
           j < 0 || j >= grid[0].length || grid[i][j] != '1'){
            return;
        }
        grid[i][j] = '2';
        infect(grid, i + 1, j);
        infect(grid, i - 1, j);
        infect(grid, i, j + 1);
        infect(grid, i, j - 1);
    }
}

228. 汇总区间

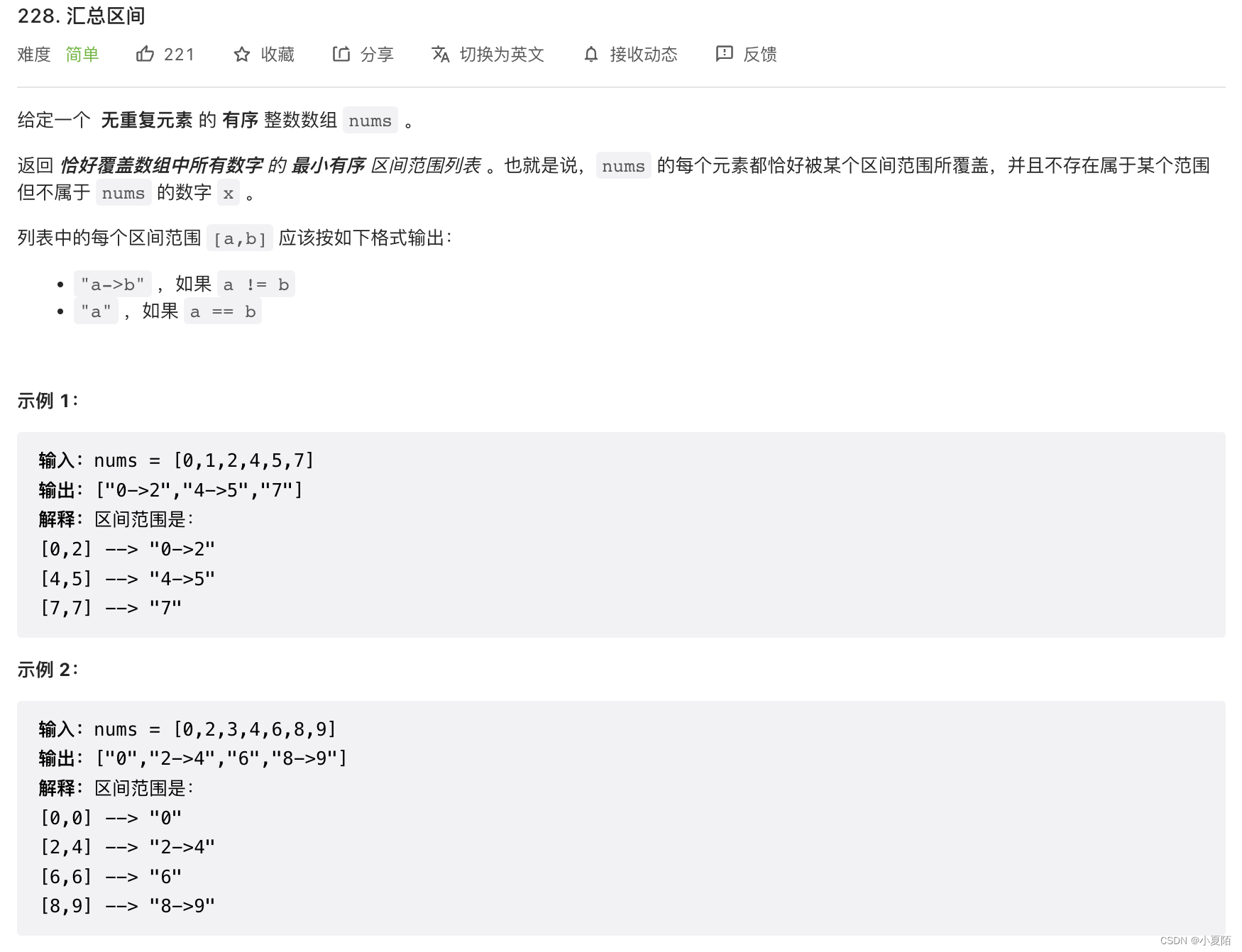
题目解析：为同一区间，拼接字符串，并添加至结果集。
代码如下：

/**
 * 数组
 */
class Solution {
    public List<String> summaryRanges(int[] nums) {
        List<String> ans = new ArrayList<String>();
        StringBuilder sb = new StringBuilder();
        for(int i = 0; i < nums.length; ++i){
            if(!(i + 1 < nums.length && nums[i] == nums[i + 1] - 1)){
                if(sb.length() > 0) sb.append("->");
                sb.append(nums[i]);
                ans.add(sb.toString());
                sb = new StringBuilder();
            } else{
                if(sb.length() == 0) sb.append(nums[i]);
            }
        }
        return ans;
    }
}

229. 求众数 II

题目解析：摩尔投票法，与摩尔投票法类似，不过需要两个候选值，当遍历数组时，候选值值相等则数量加1，不等，则两位候选值数量同时减1，当数量为0时换候选值，最后判断该值数量，是否超过三分之一。
代码如下：

/**
 * 数组 
 */
class Solution {
    public List<Integer> majorityElement(int[] nums) {
    
        List<Integer> res = new ArrayList<>();
        if (nums == null || nums.length == 0)
            return res;

        // 定义候选人和计票器
        int h1 = nums[0], count1 = 0;
        int h2 = nums[0], count2 = 0;

        for (int num : nums) {
            // 计数
            if (h1 == num) {
                count1++;
                // 每次匹配玩跳出本轮匹配
                continue;
            }

            // 计数
            if (h2 == num) {
                count2++;
                continue;
            }

            // 匹配新的候选人1
            if (count1 == 0) {
                h1 = num;
                count1++;
                continue;
            }

            // 匹配新的候选热2
            if (count2 == 0) {
                h2 = num;
                count2++;
                continue;
            }

            // 当没有匹配到当前任何候选人 并且当前候选人票数大于1时 进行票数的抵消
            count2--;
            count1--;
        }

        count1 = 0;
        count2 = 0;
        // 重新确认当前选取的候选人 票数是否超过指定票数。
        for (int num : nums) {
            if (h1 == num) count1++; // 这里必须用 else if 确保票都落在同一个人的头上
            else if (h2 == num) count2++;
        }

        if (count1 > nums.length / 3) res.add(h1);
        if (count2 > nums.length / 3) res.add(h2);

        return res;
    }
}

238. 除自身以外数组的乘积

题目解析：第一次遍历，计算所有i左边的乘积值，第二次遍历，计算所有i右边的乘积值，再乘以左边的乘积值，即为结果值。
代码如下：

/**
 * 数组
 */
class Solution {
    public int[] productExceptSelf(int[] nums) {
        int left = 1;
        int right = 1;
        int[] res = new int[nums.length];
        // 第一遍存i左边所有结点的乘积
        for (int i = 0; i < nums.length; i++) {
            res[i] = left;
            left *= nums[i];
        }
        // 第二遍倒序，计算当前i右边所有节点的乘积，
        // 调用之前计算的左边的乘积，并替换为左右乘积
        for (int i = nums.length - 1; i >= 0; i--) {
            res[i] *= right;
            right *= nums[i];
        }
        return res;
    }
}

240. 搜索二维矩阵 II

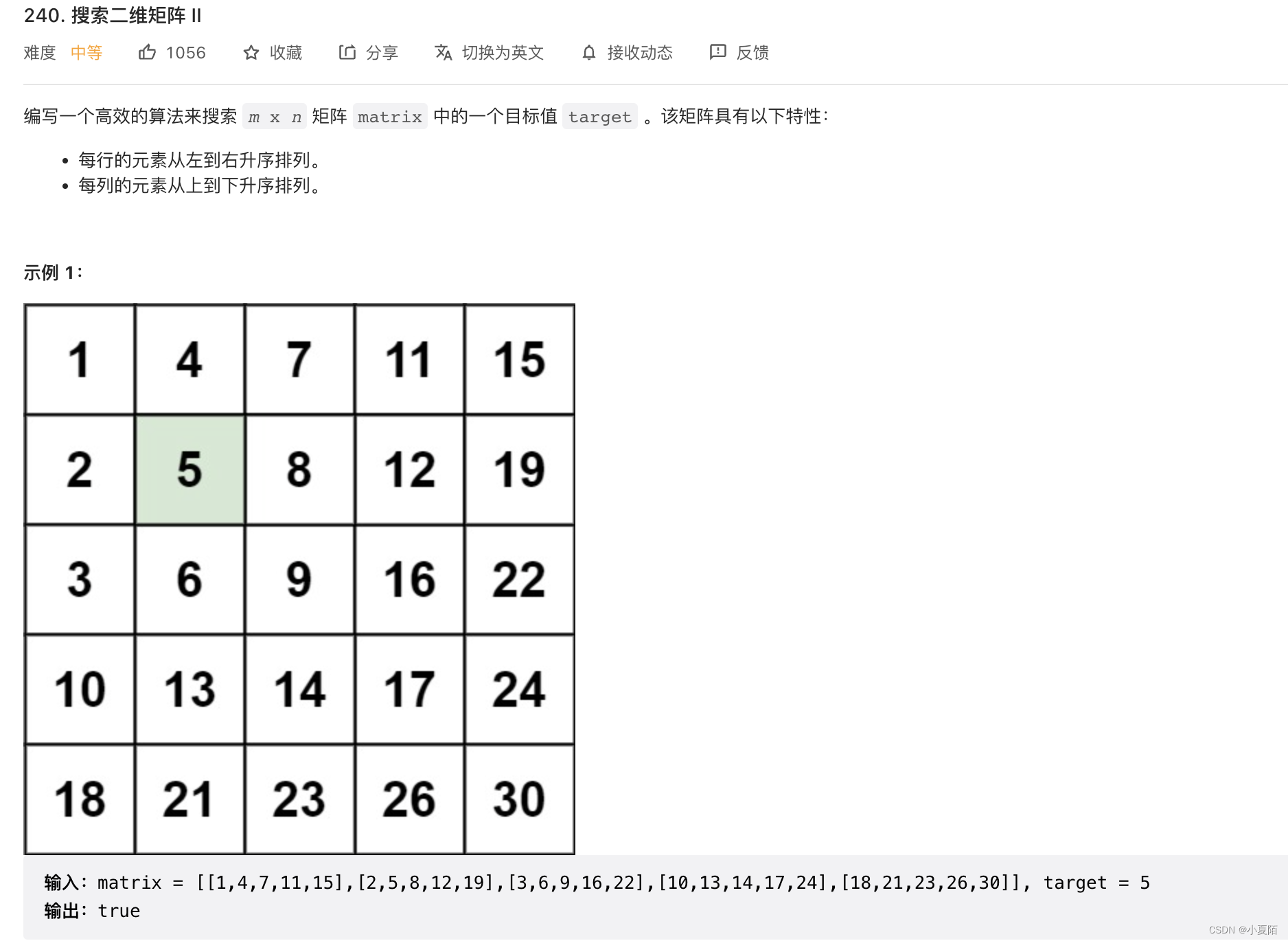
题目解析：从右上角看，是一颗二叉查找树。
代码如下：

/**
 * 二分法查找
 */
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0) return false;
        int m = 0;
        int n = matrix[0].length - 1;
        while (m < matrix.length && n >= 0) {
            if (matrix[m][n] == target) {
                return true;
            } else if (matrix[m][n] > target) {
                n--;
            } else {
                m++;
            }
        }
        return false;
    }
}

回到首页

刷 leetcode 500+ 题的一些感受

下一篇

[xxxxx]