[数据结构与算法]数据结构与算法拾遗十（一些基本的数据结构）

链表中删除某个值并返回

	public static Node removeValue(Node head, int num) {
		// head来到第一个不需要删的位置
		while (head != null) {
			if (head.value != num) {
				break;
			}
			head = head.next;
		}
		// 1 ) head == null
		// 2 ) head != null
		Node pre = head;
		Node cur = head;
		while (cur != null) {
		//定义两个指针，pre为不等于num的节点，让cur指针去遍历找，如果遇到等于num的节点则
		//将pre的next指向cur的next，如果cur不等于num则让pre=cur当前节点
			if (cur.value == num) {
				pre.next = cur.next;
			} else {
				pre = cur;
			}
			cur = cur.next;
		}
		return head;
	}

数组模拟队列

代码如下：
从pushi位置加元素，从polli位置取出元素，模拟一个环形数组

	public static class MyQueue {
		private int[] arr;
		private int pushi;// end
		private int polli;// begin
		private int size;
		private final int limit;

		public MyQueue(int limit) {
			arr = new int[limit];
			pushi = 0;
			polli = 0;
			size = 0;
			this.limit = limit;
		}

		public void push(int value) {
			if (size == limit) {
				throw new RuntimeException("队列满了，不能再加了");
			}
			size++;
			arr[pushi] = value;
			pushi = nextIndex(pushi);
		}

		public int pop() {
			if (size == 0) {
				throw new RuntimeException("队列空了，不能再拿了");
			}
			size--;
			int ans = arr[polli];
			polli = nextIndex(polli);
			return ans;
		}

		public boolean isEmpty() {
			return size == 0;
		}

		// 如果现在的下标是i，返回下一个位置
		private int nextIndex(int i) {
			return i < limit - 1 ? i + 1 : 0;
		}

	}

实现一个特殊的栈，在基本的功能的基础上，再返回栈中最小元素的功能

（1）pop、push、getMin操作的时间复杂度都是O(1)
(2)设计的栈类型可以使用现成的栈结构
思路1：
设计两个栈，一个最小栈一个数据栈，如果当前数小于等于最小栈的栈顶元素，则将当前数放入最小栈中，否则最小栈不加元素，当弹出元素的时候，如果当前数等于最小栈的栈顶元素的时候则弹出最小栈的栈顶元素否则不弹出。

思路2：
设计两个栈，一个数据栈，还有一个最小栈，如果当前数大于最小栈的栈顶元素，则重复压入最小栈的栈顶元素，如果当前数小于栈顶元素，则把当前数压入最小栈，弹出的时候则让最小栈跟着数据栈一起弹出就好了。（相当于是一种同步记录）

两种思路的代码如下所示：

public static class MyStack1 {
		private Stack<Integer> stackData;
		private Stack<Integer> stackMin;

		public MyStack1() {
			this.stackData = new Stack<Integer>();
			this.stackMin = new Stack<Integer>();
		}

		public void push(int newNum) {
			if (this.stackMin.isEmpty()) {
				this.stackMin.push(newNum);
			} else if (newNum <= this.getmin()) {
				this.stackMin.push(newNum);
			}
			this.stackData.push(newNum);
		}

		public int pop() {
			if (this.stackData.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			int value = this.stackData.pop();
			if (value == this.getmin()) {
				this.stackMin.pop();
			}
			return value;
		}

		public int getmin() {
			if (this.stackMin.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			return this.stackMin.peek();
		}
	}

	public static class MyStack2 {
		private Stack<Integer> stackData;
		private Stack<Integer> stackMin;

		public MyStack2() {
			this.stackData = new Stack<Integer>();
			this.stackMin = new Stack<Integer>();
		}

		public void push(int newNum) {
			if (this.stackMin.isEmpty()) {
				this.stackMin.push(newNum);
			} else if (newNum < this.getmin()) {
				this.stackMin.push(newNum);
			} else {
				int newMin = this.stackMin.peek();
				this.stackMin.push(newMin);
			}
			this.stackData.push(newNum);
		}

		public int pop() {
			if (this.stackData.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			this.stackMin.pop();
			return this.stackData.pop();
		}

		public int getmin() {
			if (this.stackMin.isEmpty()) {
				throw new RuntimeException("Your stack is empty.");
			}
			return this.stackMin.peek();
		}
	}

宽度优先遍历用栈实现，深度优先遍历用队列实现

如何用栈结构实现队列结构

思路：用两个栈互相倒，准备一个push栈和一个pop栈，从push栈里面加元素，如果
要弹出元素的时候则将push栈元素依次放入pop栈(push栈所有数据到pop栈)，然后再弹出去。
此时push栈是空的，再来数据的话不用将pop栈的数据倒入push栈（直到pop栈为空为止）
代码如下：

	public static class TwoStacksQueue {
		public Stack<Integer> stackPush;
		public Stack<Integer> stackPop;

		public TwoStacksQueue() {
			stackPush = new Stack<Integer>();
			stackPop = new Stack<Integer>();
		}

		// push栈向pop栈倒入数据
		private void pushToPop() {
			if (stackPop.empty()) {
				while (!stackPush.empty()) {
					stackPop.push(stackPush.pop());
				}
			}
		}

		public void add(int pushInt) {
			stackPush.push(pushInt);
			pushToPop();
		}

		public int poll() {
			if (stackPop.empty() && stackPush.empty()) {
				throw new RuntimeException("Queue is empty!");
			}
			pushToPop();
			return stackPop.pop();
		}

		public int peek() {
			if (stackPop.empty() && stackPush.empty()) {
				throw new RuntimeException("Queue is empty!");
			}
			pushToPop();
			return stackPop.peek();
		}
	}

如何用队列结构实现栈结构

思路：通过两个队列来实现，首先将数加到队列1中，如果要弹出元素的时候，则将队列1除最后一个元素外其他元素均放入队列2中，弹出队列1中剩余的最后一个元素。然后再让队列1变为队列2，队列2变成队列1，以此反复执行，得到最终的结果。

	public static class TwoQueueStack<T> {
		public Queue<T> queue;
		public Queue<T> help;

		public TwoQueueStack() {
			queue = new LinkedList<>();
			help = new LinkedList<>();
		}

		public void push(T value) {
			queue.offer(value);
		}

		public T poll() {
			while (queue.size() > 1) {
				help.offer(queue.poll());
			}
			T ans = queue.poll();
			Queue<T> tmp = queue;
			queue = help;
			help = tmp;
			return ans;
		}

		public T peek() {
			while (queue.size() > 1) {
				help.offer(queue.poll());
			}
			T ans = queue.poll();
			help.offer(ans);
			Queue<T> tmp = queue;
			queue = help;
			help = tmp;
			return ans;
		}

		public boolean isEmpty() {
			return queue.isEmpty();
		}

	}

理解递归

任何递归都可以改成非递归的代码

通过递归找数组中的最大值

思路：首先数组范围是从L到R的，再找到一个中点mid，在L到mid上找到max左，在mid+1到R中找到max右。

是怎么跑的呢
如arr为 5 6 7 2
调用函数f(arr,0,3);
1、L不等于R
2、找到mid = 1；
3、leftMax = 子过程f(0,1);
4、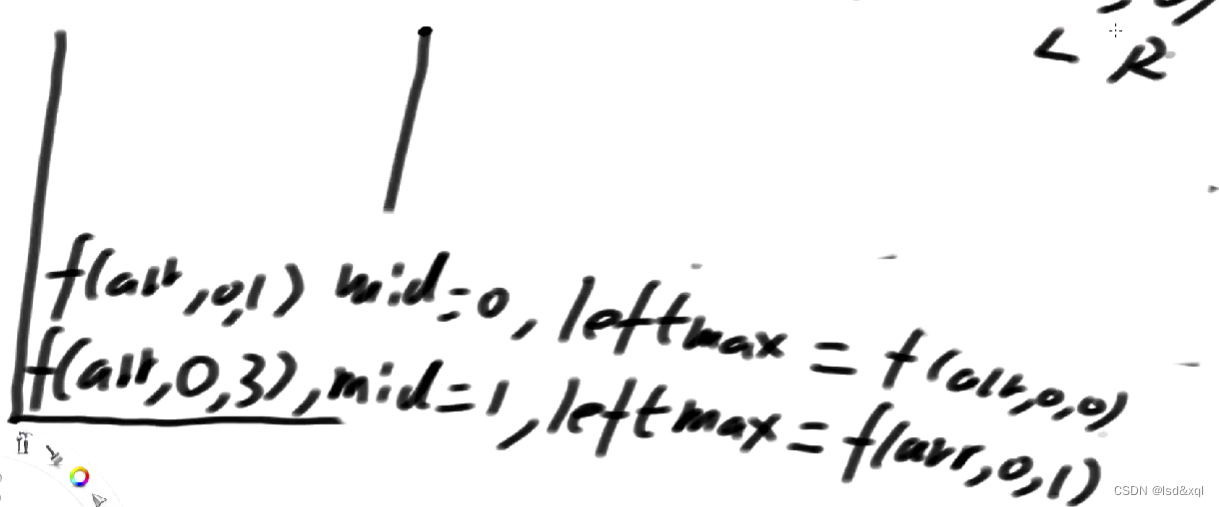
如上f(arr,0,1)分解出子过程f(arr,0,0),
f(arr,0,0)得到结果为5，然后返回到
f(arr,0,1) 并且leftmax = 5
然后执行rightmax = f(arr,1,1),这样返回rightmax = 6；
再还原f(arr,0,1) mid = 0 left = 5 right = 6，求得当前最大值为6，然后弹出f(arr,0,1)
然后再到f(arr,0,3) mid= 1 leftmax=f(arr,0,1)=6,然后开始求rightmax= f(arr,2,3)找到最大的值为7，
再回到f(arr,0,3)求得max为7，然后再弹出f(arr,0,3),流程结束，返回最大值为7
递归也可以画出如下图示：

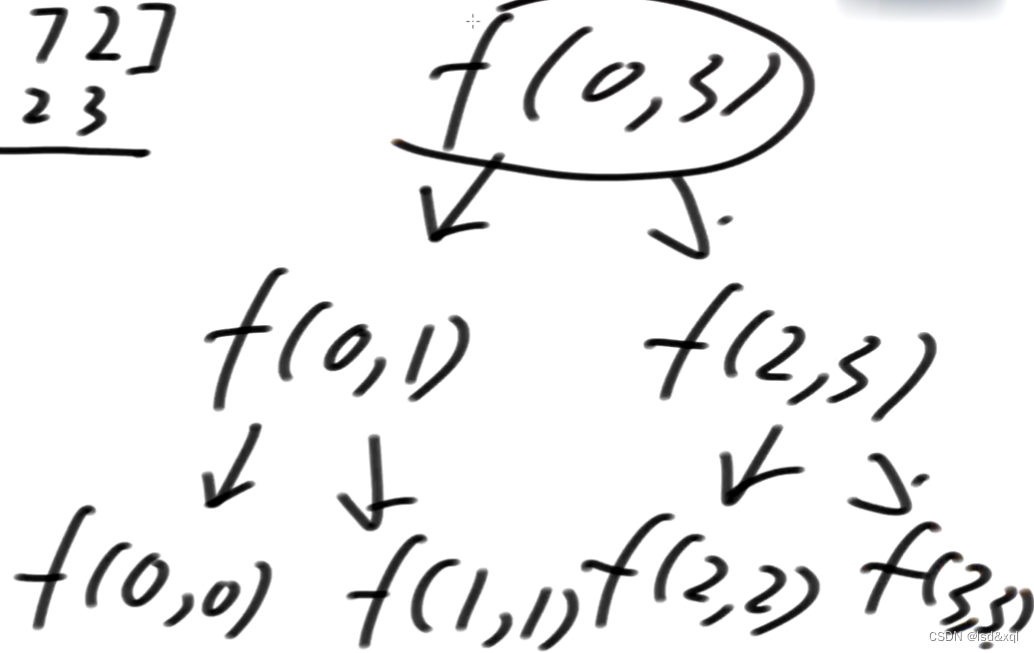
	// 求arr中的最大值
	public static int getMax(int[] arr) {
		return process(arr, 0, arr.length - 1);
	}

	// arr[L..R]范围上求最大值  L ... R   N
	public static int process(int[] arr, int L, int R) {
		// arr[L..R]范围上只有一个数，直接返回，base case
		if (L == R) { 
			return arr[L];
		}
		// L...R 不只一个数
		// mid = (L + R) / 2
		int mid = L + ((R - L) >> 1); // 中点   	1
		int leftMax = process(arr, L, mid);
		int rightMax = process(arr, mid + 1, R);
		return Math.max(leftMax, rightMax);
	}

Master公式（求递归复杂度）

前提：
子问题规模一样
形如 T(N) = a * T(N/b) + O(N^d)(其中的a、b、d都是常数)
的递归函数，可以直接通过Master公式来确定时间复杂度
如果 log(b,a) < d，复杂度为O(N^d)
如果 log(b,a) > d，复杂度为O(N^log(b,a))
如果 log(b,a) == d，复杂度为O(N^d * logN)

如上求数组最大值：
T(N) = 2T(N/2)【子过程的数据量子过程发生次数】+O(1)（除了递归行为之外剩下所有行为的时间复杂度）
a = 2 b = 2 d = 0
可求得复杂度为O(N)

hash表

增删改查O(1)

哈希表对于基础数据类型是按值传递的（如Integer和String这些）
如果对于自定的对象是按照引用传递的，hash表里面存的是内存地址
内存地址的大小一般是8字节

有序表

TreeMap （底层红黑树实现），增删改查O(logN)

public static class Node {
		public int value;

		public Node(int v) {
			value = v;
		}
	}

	public static class Zuo {
		public int value;

		public Zuo(int v) {
			value = v;
		}
	}

	public static void main(String[] args) {

		HashMap<Integer, String> test = new HashMap<>();
		Integer a = 19000000;
		Integer b = 19000000;
		System.out.println(a == b);

		test.put(a, "我是3");
		System.out.println(test.containsKey(b));

		Zuo z1 = new Zuo(1);
		Zuo z2 = new Zuo(1);
		HashMap<Zuo, String> test2 = new HashMap<>();
		test2.put(z1, "我是z1");
		System.out.println(test2.containsKey(z2));

		// UnSortedMap
		HashMap<Integer, String> map = new HashMap<>();
		map.put(1000000, "我是1000000");
		map.put(2, "我是2");
		map.put(3, "我是3");
		map.put(4, "我是4");
		map.put(5, "我是5");
		map.put(6, "我是6");
		map.put(1000000, "我是1000001");

		System.out.println(map.containsKey(1));
		System.out.println(map.containsKey(10));

		System.out.println(map.get(4));
		System.out.println(map.get(10));

		map.put(4, "他是4");
		System.out.println(map.get(4));

		map.remove(4);
		System.out.println(map.get(4));

		// key
		HashSet<String> set = new HashSet<>();
		set.add("abc");
		set.contains("abc");
		set.remove("abc");

		// 哈希表，增、删、改、查，在使用时，O（1）

		System.out.println("=====================");

		Integer c = 100000;
		Integer d = 100000;
		System.out.println(c.equals(d));

		Integer e = 127; // - 128 ~ 127
		Integer f = 127;
		System.out.println(e == f);

		HashMap<Node, String> map2 = new HashMap<>();
		Node node1 = new Node(1);
		Node node2 = node1;
		map2.put(node1, "我是node1");
		map2.put(node2, "我是node1");
		System.out.println(map2.size());

		System.out.println("======================");

		// TreeMap 有序表：接口名
		// 红黑树、avl、sb树、跳表
		// O(logN)
		System.out.println("有序表测试开始");
		TreeMap<Integer, String> treeMap = new TreeMap<>();

		treeMap.put(3, "我是3");
		treeMap.put(4, "我是4");
		treeMap.put(8, "我是8");
		treeMap.put(5, "我是5");
		treeMap.put(7, "我是7");
		treeMap.put(1, "我是1");
		treeMap.put(2, "我是2");

		System.out.println(treeMap.containsKey(1));
		System.out.println(treeMap.containsKey(10));

		System.out.println(treeMap.get(4));
		System.out.println(treeMap.get(10));

		treeMap.put(4, "他是4");
		System.out.println(treeMap.get(4));

		// treeMap.remove(4);
		System.out.println(treeMap.get(4));

		System.out.println("新鲜：");

		System.out.println(treeMap.firstKey());
		System.out.println(treeMap.lastKey());
		// <= 4 离4最近的key
		System.out.println(treeMap.floorKey(4));
		// >= 4 离4最近的key
		System.out.println(treeMap.ceilingKey(4));
		// O(logN)

	}