[数据结构与算法]leetcode：968. 监控二叉树【树状dp，维护每个节点子树的三个状态，非常难想权当学习，类比打家劫舍3】

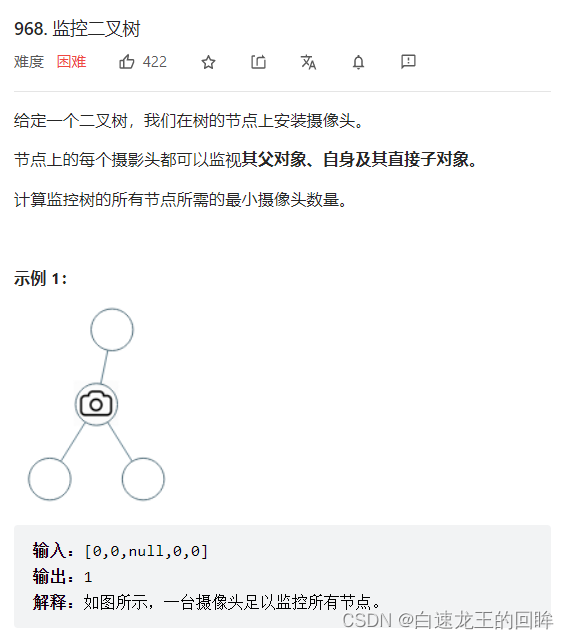
分析

三个状态，记录每个节点为根的子树：
状态 a：root 必须放置摄像头的情况下，覆盖整棵树需要的摄像头数目。
状态 b：覆盖整棵树需要的摄像头数目，无论 root 是否放置摄像头。
状态 c：覆盖两棵子树需要的摄像头数目，无论节点 root 本身是否被监控到。
a >= b >= c

a = lc + rc + 1
b = min(a, la + rb, ra + lb)
c = min(a, lb + rb)

式子1：当前根放了，只需覆盖两个子树就可以了（要求较低）
式子2：如果放了root就是a，如果不放那左右孩子至少有一个放，左放右随缘la + rb, 右放左随缘ra + lb
式子3：如果放了root就是a，如果不放，就是两个子树覆盖的的可能即可

如果是空的话，显然是不能选的，所以a填inf

ac code

class Solution:
    def minCameraCover(self, root: TreeNode) -> int:
        # 树状dp：三个状态（难以想象）
        # 状态 a：root 必须放置摄像头的情况下，覆盖整棵树需要的摄像头数目。
        # 状态 b：覆盖整棵树需要的摄像头数目，无论 root 是否放置摄像头。
        # 状态 c：覆盖两棵子树需要的摄像头数目，无论节点 root 本身是否被监控到。
        # a >= b >= c

        def dfs(root: TreeNode) -> List[int]:
            if not root:
                return [float("inf"), 0, 0] # 不可能放，用inf
            
            la, lb, lc = dfs(root.left)
            ra, rb, rc = dfs(root.right)
            a = lc + rc + 1
            b = min(a, la + rb, ra + lb)
            c = min(a, lb + rb)
            #print(a, b, c)
            return [a, b, c]
        
        a, b, c = dfs(root)
        return b

总结

树状dp板子题
如何想到那三个状态呢？望洋兴叹！