1. 问题描述

假如我们有一个背包，在我们面前摆了 i 件物品，这些物品的价值分别为 v,
怎么装可以保证背包里所有物品加起来价值最大。（注意：一件物品只能拿一次）

2. 0/1是什么意思呢？

0代表这个物品不拿，1代表这个物品拿，其实就代表着拿和不拿的问题

3. 分析

有三个物品，它们的重量分别为1，3，2 价值为：1，4，3
现在有个容量为4的背包，怎么装可以保证所装入物品价值总和最大？

物品价值数组: int v[4]={0,1,4,3};
物品重量数组: int w[4]={0,1,3,2};
物品:i 包容量:j 在这里插入图片描述其实就是比较背包的容量和物品的重量，分为两种情况：

如果包的容量大于等于物品容量：j>=w[i]
可以拿，这个时候又分为两种情况，我拿还是不拿，其实就是比较谁的价值大，拿价值大的
第一种情况：
?????????????????不拿：上一个物品的价值(直接往上看一行 ) dp[i-1][j]。例如：包容量为4，物品为3时，直接看上一行价值5.
第二种情况：
?????????????????拿：dp[i-1][j-w[i]]+v[i]。例如：包容量为2，物品为3时，dp[2-1][2-2]+3=3。
如果包容量小于物品重量：j<w[i]
包装不下物品（不足以放下），相当于不装，不拿的价值就是上一个物品的价值 dp[i][j] = dp[i-1][j]
例如：包容量为1，商品为2时，就是上一个物品的价值1

if(j>=w[i])//如果包的容量大于等于物品容量 
	dp[i][j] = max(v[i]+dp[i-1][j-w[i]],dp[i-1][j]);//状态转移方程 
else 
	dp[i][j] = dp[i-1][j];//包容量小于(装不下)物品容量，相当于不装

状态转移方程：

 dp[i][j] = max(v[i]+dp[i-1][j-w[i]],dp[i-1][j]);
 
 dp[1][0] ：背包容量为0时 装第1个物品，它的价值为多少

dp[i][j] = max(装它，不装它); 比较看装它还是不装它的价值大

装它
v[i]: 物品本身的价值
j-w[i]：包容量减去物品容量
dp[i-1][j-w[i]]：回到上一行看，剩余背包容量的最大价值
不装它
dp[i-1][j]：直接往上看一行

4. 代码

#include <iostream>
using namespace std;


int main(){
	int v[4]={0,1,4,3};//物品价值 
	int w[4]={0,1,3,2};//物品重量 
	int dp[10][10] = {0}; //记录状态
	// dp[ i ][ j ]  表示第i件物品，背包容量为 j时的最大价值  
	for(int i=1;i<4;i++){//物品 
		for(int j=1;j<=4;j++){//包容量 
			if(j>=w[i]){//如果包的容量大于等于物品容量 
				dp[i][j] = max(v[i]+dp[i-1][j-w[i]],dp[i-1][j]);//状态转移方程 
			}else dp[i][j] = dp[i-1][j];//包容量小于(装不下)物品容量，相当于不装
			cout<<dp[i][j]<<" "; 
		}
		cout<<endl;
	}
	return 0;
}

5. 滚动数组

把二维dp数组压缩为一维dp数组，就用到了滚动数组，就是每运行一遍，就去刷新一下dp数组，让状态转移方程式更简单。

用 n-1 状态的一维dp数组作为 n状态的一维数组， n状态的一维数组作为 n+1状态的一维数组（n+1只和n有关系，和n-1没有关系。）如果要装n个物品的最大价值，需要将列表重新覆盖（列表就是按照这种方式不断的滚动刷新）

#include <iostream>
using namespace std;


int main(){
	int v[4]={0,1,4,3};//物品价值 
	int w[4]={0,1,3,2};//物品重量 
	int dp[10] = {0}; //记录状态 
	for(int i=1;i<4;i++){//物品 
		for(int j=4;j>=1;j--){//逆向推，用到上一条的旧数据
			if(j>=w[i])
				dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
		}
		for(int k=0;k<=4;k++){
			cout<<dp[k]<<" ";
		}
		cout<<endl;
	}
	return 0;
}

打印结果如下所示：
在这里插入图片描述

#include <iostream>
using namespace std;


int main(){
	int v[4]={0,1,4,3};//物品价值 
	int w[4]={0,1,3,2};//物品重量 
	int dp[10] = {0}; //记录状态
	for(int i=1;i<4;i++){//物品 
		for(int j=4;j>=w[i];j--){//逆向推，用到上一条的旧数据
			dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
	cout<<dp[3];
	return 0;
}

6. 练习

【题目描述】

一个旅行者有一个最多能装 M公斤的背包，现在有 n 件物品，它们的重量分别是W1，W2，...,Wn,
它们的价值分别为C1,C2,...,Cn，求旅行者能获得最大总价值。

【输入】

第一行：两个整数，M(背包容量，M<=200)和N(物品数量，N<=30)；
第2..N+1行：每行二个整数Wi，Ci，表示每个物品的重量和价值。

【输出】

仅一行，一个数，表示最大总价值。

【输入样例】
10 4
2 1
3 3
4 5
7 9

【输出样例】
12

dp数组输出样例：

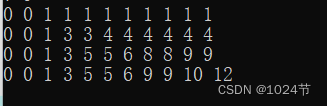
在这里插入图片描述

#include <iostream>
using namespace std;

int w[35],c[35],dp[205];
int main(){
	int m,n;//m背包容量，n物品数量 
	cin>>m>>n;
	for(int i=1;i<=n;i++){
		cin>>w[i]>>c[i];//Wi：物品的重量  Ci：物品的价值 
	}
	for(int i=1;i<=n;i++){//物品
		for(int j=m;j>=1;j--){//逆向推，用到上一条的旧数据
			if(j>=w[i]){
				dp[j] = max(dp[j],dp[j-w[i]]+c[i]);
			}
		}
		for(int k=0;k<=m;k++){ 
			cout<<dp[k]<<" "; //打印dp数组 
		}
		cout<<endl;
	}
	return 0;
}