? ? ? ? 万里之行,始于足下。本博客总结近期学习到的部分数据结构模板,以便于日后查询使用。作者水平有限,难免存在疏漏不足,恳请诸位看官斧正。倘若我的文章可以帮到你,十分荣幸。当然,笔者以后会对本文更新优化。本次内容的灵感来自于最近暑期训练对线段树内容的回顾。
目录
1.引经据礼——何谓线段树?
? ? ? ?学习过树状数组的同学知道,树状数组很能够方便快捷地实现区间的前缀和查询与单点修改。但是它的本质仍然是前缀和,所以它依赖了前缀和的“前缀可减性”,单点修改操作具有一定的局限性。例如,如何维护区间最大值、最小值?而且,如果我们想更方便一点,一次修改一个区间的数呢?例如:洛谷-P3372 【模板】线段树 1
? ? ? 于是就有了今天的主角,线段树。线段树是一种二叉搜索树,与区间树相似,它将一个区间对半划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为。
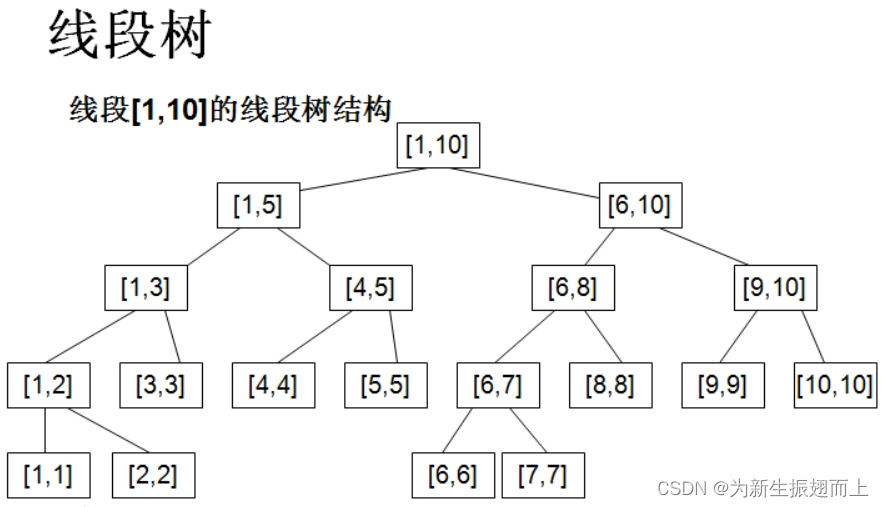
线段树示意图(来源:百度百科)?
? ? ? ?愚以为,线段树的核心思想是对于一个区间[l,r],我们可以令mid=(l+r)/2,将它分成[l,mid]和[mid+1,r]两个部分,如此分而治之,维护、查询完之后再如此递归处理它的子区间,之后不要忘记通过新的子区间来向上更新这个区间自己的信息。
2.抽丝剥茧——且听我逐层道来
(1)区间节点的表示
? ? ? ? 我们采用一个结构体来存储线段树的一个节点,也就是节点代表的这一段区间的数据。
struct node{
int l,r;//节点表示区间的左右端点
ll sum;//区间和
ll lazy;//lazy_tag
};? ? ? ?其中,sum是[l,r]这个区间的数据之和(因为之前我们给出的问题是快速查询区间和)。当然,如果我们需要查询其他的信息的话也需要在这里加上,比如区间乘积之类的。而lazy呢?这个关乎我们如何高效进行线段树区间修改的,后文且听我细细道来。材料有了,那我们就可以着手建立数据结构了。
(2)线段树的建树
? ? ? ?线段树的建树主要采用了递归的思想。在我们在建树函数中输入线段树的根节点信息后,对半分区间,递归构建它的左右子节点。
? ? ? ?问题来了:请思考,编号为root的二叉树左右子节点的编号是啥?
? ? ? ?数据结构知识告诉我们,在二叉树中为了便于管理,某个编号root的节点,左子节点编号为root*2,右子节点编号为root*2+1(当然,我们还可以使用位运算用root<<1表示root*2),具体原理这里不做赘述。
void build(int root,int l,int r){
t[root].l=l;
t[root].r=r;//区间左右端点
init_lazy(root);//初始化节点lazy_tag
if(l!=r){//非叶子结点,表示一段数据
int mid=(l+r)>>1;//值相当于(l+r)/2
int ch=root<<1;//子节点,值相当于root*2
build(ch,l,mid);
build(ch+1,mid+1,r);//递归建立左右子树
update(root);//根据新的左右子树更新当前节点
}else{
t[root].sum=a[l];//叶子结点,我们直接赋节点值就好了
}
}(3)lazy_tag
? ? ? ?试想一下:在修改某个区间数的时候,如果我们对每个叶子节点逐一修改,是不是会很麻烦,违背了我们一开始想高效区间维护的初衷?我们会发现,在修改的区间中,有些子区间可能从头到尾我们查询操作都没理过它,那么,我们可以“偷懒”,只是向下更新部分叶子节点的值,而其他的区间节点仅仅只是记录我们需要修改的值,并不向下更新子节点的信息,一直到我们需要用到它,再让它向下传递,更新子节点的sum和lazy的值。
? ? ? ?例如:我们需要让[2,8]这个区间的数都加上1 。覆盖了[2,2]、[3,4]和[5,8]这三个区间、那么我们就让这些被覆盖的区间节点lazy_tag加1,至于他们的子节点嘛,先等等看,不着急更新([2,2]这个是叶子节点,其实我们可以直接把修改的值给加上了)。当然,修改了这些区间节点,也别忘了向上更新他们的父节点信息(红色斜线标记)。
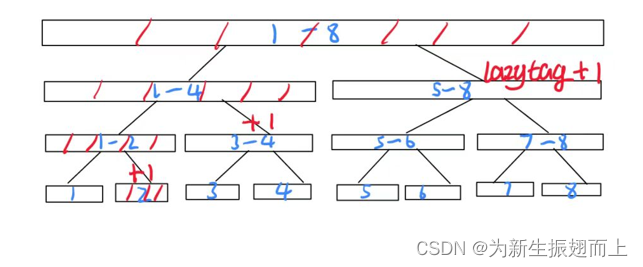
? ? ? ?之后,我们需要查询区间[5,6]的信息,但是这里的信息还是旧的,所以这个时候我们就需要用到这个区间,我们将它的父节点的lazy_tag向下传递到左右子节点。同时也需要依据lazy_tag和父节点区间长度更新父节点,也就是更新为父节点真实的信息,并重置父节点lazy_tag值。这样我们要查询的区间就可以根据先祖节点记录的lazy_tag值来计算它的真实信息了。
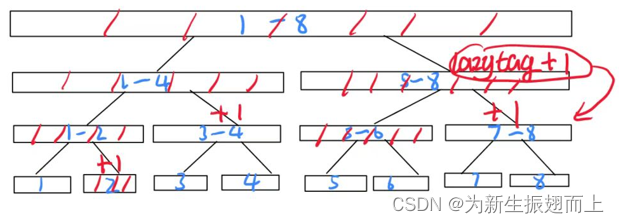
? ? ? ? 至于其他的区间如[7,8]嘛?哈哈,如果没有用到就没必要更新了,这样就省去了好多不必要操作,降低了时间复杂度。相关操作如下:
void init_lazy(int root){//初始化lazy_tag
t[root].lazy=0;
}
void union_lazy(int fa,int ch){//子节点接受父节点lazy_tag值
t[ch].lazy+=t[fa].lazy;
}
void cal_lazy(int root){//通过区间lazy_tag计算区间真实值
t[root].sum+=(t[root].r-t[root].l+1)*t[root].lazy;
}
void push_down(int root){//向下传递lazy_tag
if(t[root].lazy){
cal_lazy(root);//通过区间lazy_tag计算区间真实值
if(t[root].r!=t[root].l){//非叶子节点向下传递tag
int ch=root<<1;
union_lazy(root,ch);
union_lazy(root,ch+1);
}
init_lazy(root);//重置初始化节点lazy_tag
}
}
void update(int root){//向上更新父节点值
int ch=root<<1;
push_down(ch);
push_down(ch+1);//维护左右子节点
t[root].sum=t[ch].sum+t[ch+1].sum;
}?? ? ? ?这里为了使结构更加清晰可能函数有些冗余,为了效率我们可以直接用代码替换。init_lazy、union_lazy和cal_lazy函数在之后拓展中较为复杂的线段树问题中可以更加便利地拓展。
(4)区间查询&区间修改
?? ? ? 区间查询与修改操作的思路与代码是类似的。如上一节所述,我们递归修改/查询需要操作的区间的子区间,当然不要忘了向下传递lazy_tag。如果当前区间正好与需要操作的区间相同,那我们就可以很愉快地完成任务了。不然,我们需要将当前区间一分为二,到它的左右子节点递归精确查找到我们想要的区间。如果是修改的话,需要在最后向上更新父节点。
void change(int root,int l,int r,ll data){//修改操作
push_down(root);//向下传递lazy_tag
if(l==t[root].l&&r==t[root].r){//当前节点区间刚好是需要查找的区间
t[root].lazy+=data;//修改数据
return;
}
int mid=(t[root].l+t[root].r)>>1;//区间一分为二
int ch=root<<1;
if(r<=mid) change(ch,l,r,data);//查找区间在左半段
else if(l>mid) change(ch+1,l,r,data);//查找区间在右半段
else{//查找区间横跨当前节点区间中点,左右都有
change(ch,l,mid,data);
change(ch+1,mid+1,r,data);
}
update(root);//向上更新父节点
}
ll sum(int root,int l,int r){//查询操作(当前例题为区间和)
push_down(root);//向下传递lazy_tag
if(l==t[root].l&&r==t[root].r){//当前节点区间刚好是需要查找的区间
return t[root].sum;
}
int mid=(t[root].l+t[root].r)>>1;//区间一分为二
int ch=root<<1;
if(r<=mid) return sum(ch,l,r);//查找区间在左半段
else if(l>mid) return sum(ch+1,l,r);//查找区间在右半段
else return sum(ch,l,mid)+sum(ch+1,mid+1,r);
//查找区间横跨当前节点区间中点,左右都有
}(5)总体模板代码
??? ? ? 好,综上所述,我们已经分析了线段树最基础的结构了,那么它的例题代码就是如此。
#include <bits/stdc++.h>
#define endl '\n'
#define ll long long
using namespace std;
template<class T>inline void read(T &res){//快读
char c;T flag=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag;
}
const int maxn=1e5+7;
ll a[maxn];
struct node{
int l,r;//节点表示区间的左右端点
ll sum;//区间和
ll lazy;//lazy_tag
};
struct SegmentTree{
node t[maxn<<2];
void init_lazy(int root){//初始化lazy_tag
t[root].lazy=0;
}
void union_lazy(int fa,int ch){//子节点接受父节点lazy_tag值
t[ch].lazy+=t[fa].lazy;
}
void cal_lazy(int root){//通过区间lazy_tag计算区间真实值
t[root].sum+=(t[root].r-t[root].l+1)*t[root].lazy;
}
void push_down(int root){//向下传递lazy_tag
if(t[root].lazy){
cal_lazy(root);//通过区间lazy_tag计算区间真实值
if(t[root].r!=t[root].l){//非叶子节点向下传递tag
int ch=root<<1;
union_lazy(root,ch);
union_lazy(root,ch+1);
}
init_lazy(root);//重置初始化节点lazy_tag
}
}
void update(int root){//向上更新父节点值
int ch=root<<1;
push_down(ch);
push_down(ch+1);//维护左右子节点
t[root].sum=t[ch].sum+t[ch+1].sum;
}
void build(int root,int l,int r){
t[root].l=l;
t[root].r=r;//区间左右端点
init_lazy(root);//初始化节点lazy_tag
if(l!=r){//非叶子结点,表示一段数据
int mid=(l+r)>>1;//值相当于(l+r)/2
int ch=root<<1;//子节点,值相当于root*2
build(ch,l,mid);
build(ch+1,mid+1,r);//递归建立左右子树
update(root);//根据新的左右子树更新当前节点
}else{
t[root].sum=a[l];//叶子结点,我们直接赋节点值就好了
}
}
void change(int root,int l,int r,ll data){//修改操作
push_down(root);//向下传递lazy_tag
if(l==t[root].l&&r==t[root].r){//当前节点区间刚好是需要查找的区间
t[root].lazy+=data;//修改数据
return;
}
int mid=(t[root].l+t[root].r)>>1;//区间一分为二
int ch=root<<1;
if(r<=mid) change(ch,l,r,data);//查找区间在左半段
else if(l>mid) change(ch+1,l,r,data);//查找区间在右半段
else{//查找区间横跨当前节点区间中点,左右都有
change(ch,l,mid,data);
change(ch+1,mid+1,r,data);
}
update(root);//向上更新父节点
}
ll sum(int root,int l,int r){//查询操作(当前例题为区间和)
push_down(root);//向下传递lazy_tag
if(l==t[root].l&&r==t[root].r){//当前节点区间刚好是需要查找的区间
return t[root].sum;
}
int mid=(t[root].l+t[root].r)>>1;//区间一分为二
int ch=root<<1;
if(r<=mid) return sum(ch,l,r);//查找区间在左半段
else if(l>mid) return sum(ch+1,l,r);//查找区间在右半段
else return sum(ch,l,mid)+sum(ch+1,mid+1,r);
//查找区间横跨当前节点区间中点,左右都有
}
};
SegmentTree st;//线段树
int n,m,ins,x,y;
ll k;
int main(){
//ios::sync_with_stdio(false);
//cin.tie(0),cout.tie(0);
read(n), read(m);//快读读入n,m
for(int i=1;i<=n;i++) read(a[i]);
st.build(1,1,n);//建树
for(int i=1;i<=m;i++){
read(ins);//根据相应的标记执行查询/修改操作
if(ins==1){
read(x), read(y), read(k);
st.change(1,x,y,k);
}else if(ins==2){
read(x), read(y);
cout<<st.sum(1,x,y)<<endl;
}
}
return 0;
}??? ? ? 这里我受到牛客竞赛四系智乃的启发,采用了这一种比较“面向对象”的线段树模式,结构比较清晰合理,也易于勘误debug。
3.长虑顾后——关于线段树的一些问题的讨论
(1)线段树的单点修改
??? ? ? 线段树功能如此强大,那我们怎么对它进行单点修改呢?我们知道数据的单点对应着线段树的叶子结点,那么我们需要在建树的时候使用一个数组记录映射关系,即每个单点在数据(例如数组)中的序号到线段树节点编号的映射,这样我们就可以找到节点数组需要修改的位置。在修改完成之后,我们需要向上更新它所有的先祖节点,根据我们之前了解的二叉树的性质,设叶子节点编号为n,那我们就用while(n>>1)(或者说是while(n/2))对它的先祖节点遍历更新。实现代码如下:
void change(int x,int y){
int ind=mp[x];//获得映射关系
if(t[ind].sum<y){
t[ind].sum=y;
while(ind){
ind>>=1;
update(ind);//循环更新先祖节点
}
}
}(2)线段树多lazy_tag的后效性
??? ? ? 在一些题目中,我们需要考虑的操作可能不止一种,那么我们就自然而然的想到了加入多个lazy_tag,例如牛客竞赛-数据结构,我们需要对区间进行加/乘两种不同的修改操作,设置了两个lazy_tag。但是这可能会给我们的push_down操作带来一定的麻烦:
? ? ? ? 第一步,[5,8]区间乘3,那么3号节点的乘lazy_tag改为3。第二步,[5,6]区间加1,那么6号节点的加lazy_tag改为1。问题来了:在push_down操作中,[5,6]区间的值是先加1,之后才乘3,和我们期望的顺序相反。3(x+1)和3x+1是不同的,所以在此类多lazy_tag问题中我们需要合理处理lazy_tag的后效性。
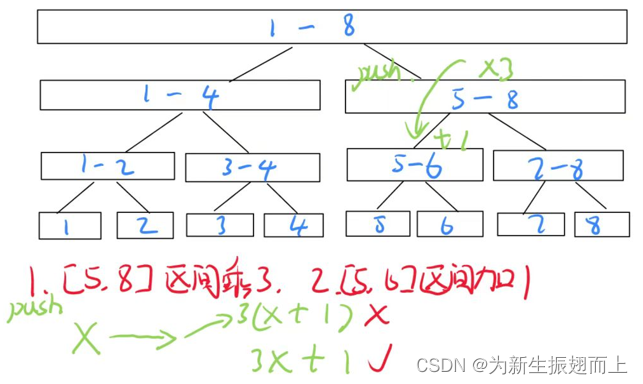
? ? ? ??这个时候我们之前提到过的在模板例题中看似冗余的init_lazy、union_lazy和cal_lazy函数派上了用场。
定义节点
struct node{
ll sum,square;//区间和与区间平方和
ll add,mul;//加、乘lazy_tag
int l,r;
};init_lazy函数
? ? ? ??注意mul初值为1,因为对应的是乘法操作。
void init_lazy(int root){
t[root].add=0;
t[root].mul=1;
}cal_lazy函数
? ? ? ??利用lazy_tag计算当前点和与平方和的真实值,推导如下:

? ? ? ??其中a代表加的lazy_tag,m代表乘lazy_tag。那么我们可以得到如下代码:
void cal_lazy(int root) {
t[root].sum=t[root].mul*t[root].sum+(t[root].r+t[root].l-1)*t[root].add;
t[root].square=t[root].mul*t[root].mul*t[root].square+
2*t[root].mul*t[root].add*t[root].sum+
(t[root].r-t[root].l+1)*t[root].add*t[root].add;
return;
}? ? ? ??虽然看起来挺复杂,但是理解了线段树原理推导过程还是比较容易的。
union_lazy函数
? ? ? ? 利用union_lazy合理处理lazy_tag之间的“关系”,向下传递给子节点。推导如下:
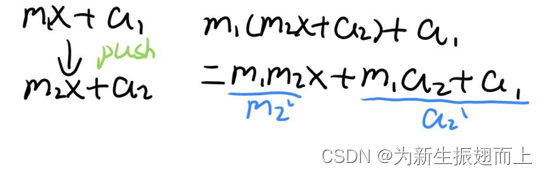
? ? ? ? 1下标为父节点,2下标为子节点(当然这里只画了一个子节点) 。得到代码如下:
void union_lazy(int fa, int ch){//fa为父节点,ch为子节点
t[ch].add=t[fa].mul*t[ch].add+t[fa].add;
t[ch].mul=t[fa].mul*t[ch].mul;
}? ? ? ?综上,我们可以在原有的基础题上灵活改动,处理多修改多操作问题,做到“以不变应万变”。
4.来日正长——接下来我要学习的
? ? ? ?“艰难方显勇毅,磨砺始得玉成。”这次我重新捡起了一下去年学习的线段树,温故知新,收获颇丰。作为团队数据结构选手可能在接下来会巩固学习线段树的进阶操作:李超线段树、DDP等相关知识。同样的还有一些我提到的基础数据结构如前缀和、树状数组我也需要重温,所以我在中标题加入了(上)。那么感谢你能够看到最后,见证了我又一个成长的脚印。