[数据结构与算法]AtCoder Beginner Contest 254「E bfs」「F st表维护差分数组gcd」

AtCoder Beginner Contest 254

E - Small d and k

题目描述：

给你一个无向图，每个点的度数最多为3，进行Q次询问，每次询问都给x,k,表示询问以x为起点，距离小于等于k步的点的id的和

其中k<=3

思路：

因为度最多为3，且k<=3，所以每次询问最多就涉及到27个点，27 * Q也才4e6，复杂度说的过去，我们之间暴力跑bfs就行

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod7 1000000007
#define mod9 998244353
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define debug(a) cout << "Debuging...|" << #a << ": " << a << "\n";
typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k, x, y;
vector<int>G[MAX];
bool vis[MAX];
void work(){
    cin >> n >> m;
    for(int i = 1; i <= m; ++i){
        cin >> x >> y;
        G[x].push_back(y);
        G[y].push_back(x);
    }
    cin >> m;
    while(m--){
        cin >> x >> k;
        if(k == 0){
            cout << x << endl;
            continue;
        }
        vector<int>v;
        queue<pii>q;
        q.push(m_p(x, k));
        vis[x] = 1;
        while(!q.empty()){
            auto [u, d] = q.front();q.pop();
            v.push_back(u);
//            cout << u << ' ' << d << endl;
            for(auto v : G[u]){
                if(!vis[v] && d){
                    q.push(m_p(v, d - 1));
                    vis[v] = 1;
                }
            }
        }
        int ans = 0;
        for(auto x : v){
            ans += x;
            vis[x] = 0;
        }
        cout << ans << endl;
    }
}


int main(){
    io;
    work();
    return 0;
}

F - Rectangle GCD

题目描述：

给你两个数组ar,br，长度都是n,定一个一个n*n的矩阵C,其中C[i][j] = ar[i] + br[j],现在给你Q次询问，每次询问都给你一个小矩形的左上角和右下角，问这个小矩形的所有元素的gcd

思路：

首先要清楚一个序列所有元素的最大公约数等于差分数组的最大公约数 ，即$gcd(a[1],a[2],...,a[n])=gcd(a[1],a[2]?a[1],a[3]?a[2],...,a[n]?a[n?1])$

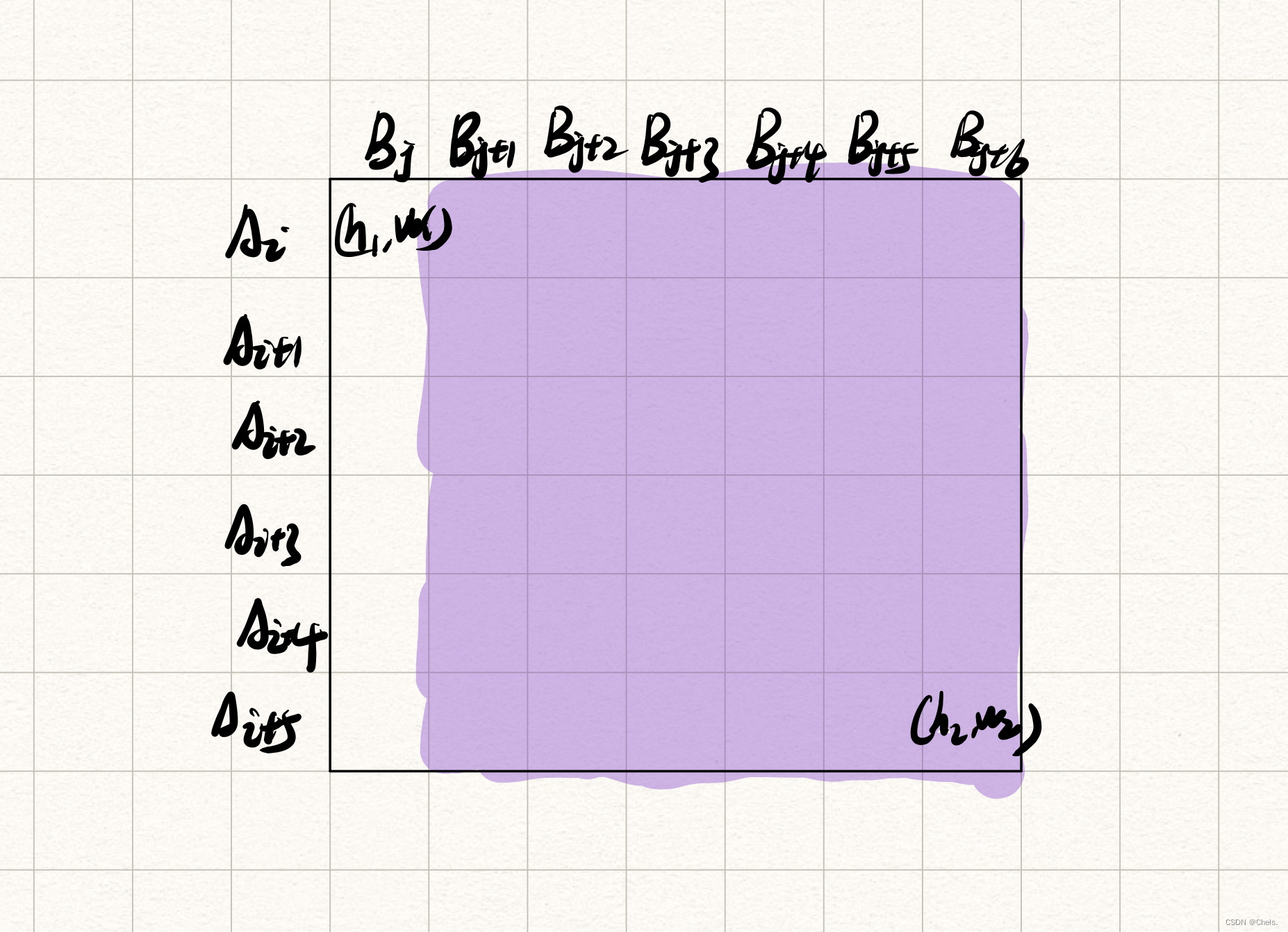
所以我们考虑查询区间的第i行

$gcd(a[i]+b[j],a[i+1]+b[j],a[i+2]+b[j],....)=gcd(a[i]+b[j],a[i+1]?a[i],a[i+2]?a[i+1]...)$ 我们先不看a[i]+b[j]，则根据后面的那段的gcd，我们可以通过求gcd(a[i+1]-a[i], a[i+2]-a[i+1]...)获得下图紫色部分的所有的数字的gcd

同理，我们可以利用gcd(br[i+1]-br[i], br[i+2]-br[i+1]....)获得下面蓝色部分的所有数字的gcd

而我们需要的是从C[h1][w1]到C[h2][w2]的所有数字的gcd，综合一下图型可以发现左上角的数字没有被计算过，所以我们只需要将上面两个差分区间的gcd和C[h1][w2]也就是A[h1]+B[w1]求一个gcd即可

所以我们可以利用st表来维护差分数组的区间gcd

说实话我写的时候真没想这么深，就想到了gcd(x, y)可以转换成gcd(x-y, x)，就觉得是求差分数组的gcd，再加上光求差分数组不够，还得有个x，就加上了左上角的元素三者一起求了个gcd，背了个st表套上去没想到真的过了

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define inf 0x3f3f3f3f
#define mod7 1000000007
#define mod9 998244353
#define m_p(a,b) make_pair(a, b)
#define mem(a,b) memset((a),(b),sizeof(a))
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define debug(a) cout << "Debuging...|" << #a << ": " << a << "\n";
typedef long long ll;
typedef pair <int,int> pii;

#define MAX 300000 + 50
int n, m, k, x;
ll ar[MAX];
ll br[MAX];

ll gcd(ll a, ll b){
    if(b) return gcd(b, a % b);
    else return a;
}

ll lg[MAX];
ll g1[MAX][22];
ll g2[MAX][22];
void init(){
    for(int i = 2; i <= n; ++i){
        lg[i] = lg[i / 2] + 1;
    }
    for(int i = 2; i <= n; ++i){
        g1[i][0] = ar[i] - ar[i - 1];
        g2[i][0] = br[i] - br[i - 1];
    }
    for(int j = 1; j <= lg[n]; ++j){
        for(int i = 2; i + (1 << j) - 1 <= n; ++i){
            g1[i][j] = gcd(g1[i][j - 1], g1[i + (1 << (j - 1))][j - 1]);
            g2[i][j] = gcd(g2[i][j - 1], g2[i + (1 << (j - 1))][j - 1]);
        }
    }
}
ll get_gcd(int l, int r, int op){
    ll d = lg[r - l + 1];
    if(op)return abs(gcd(g1[l][d], g1[r - (1 << d) + 1][d]));
    else return abs(gcd(g2[l][d], g2[r - (1 << d) + 1][d]));
}



void work(){
    cin >> n >> m;
    for(int i = 1; i <= n; ++i)cin >> ar[i];
    for(int j = 1; j <= n; ++j)cin >> br[j];
    init();
    int h1, h2, w1, w2;
    while(m--){
        cin >> h1 >> h2 >> w1 >> w2;
        ll a = 0, b = 0;
        if(h1 == h2)a = 0;
        else a = get_gcd(h1 + 1, h2, 1);
        if(w1 == w2)b = 0;
        else b = get_gcd(w1 + 1, w2, 0);
        cout << gcd(a, gcd(b, ar[h1] + br[w1])) << endl;
    }
}


int main(){
    io;
    work();
    return 0;
}