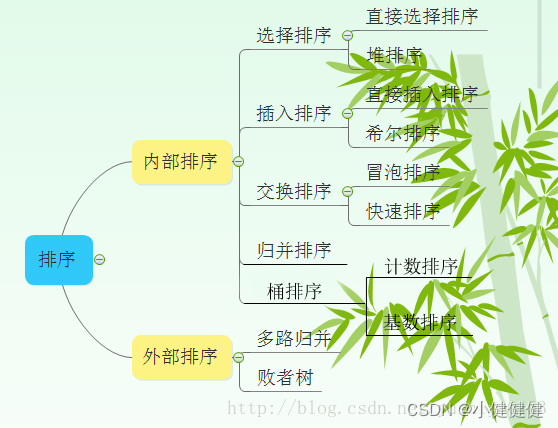
选择排序
直接选择排序
时间复杂度O(n^2)
空间复杂度O(1)
稳定
final static class selectSort{
public selectSort(int[] arr){
Sort(arr, arr.length);
}
private void Sort(int[] arr, int n) {
for (int i = 0; i < n; i++) {
int min = i;
for (int j = i; j < n; j++) {
if(arr[min] > arr[j]){
min = j;
}
}
swap(arr, i, min);
}
}
}
堆排序
时间复杂度不太好算啊,看看这个:https://blog.csdn.net/YuZhiHui_No1/article/details/44258297
建堆时间复杂度O(n)
堆排序时间复杂度O(nlogn)
空间复杂度O(1)
final static class heapSort{
//堆排序用new PriorityQueue<Integer>((o1, o2)->(o1 - o2));
//https://www.runoob.com/w3cnote/heap-sort.html
//https://zhuanlan.zhihu.com/p/45725214
public heapSort(int[] arr){
if(arr.length < 2) return;
int len = arr.length;
BuildMaxHeap(arr, len);
for(int i=len-1; i>0; i--){
swap(arr, 0, i);
len--;
heapify(arr, 0, len);
}
}
public void BuildMaxHeap(int[] arr, int len){
for(int i=(int) Math.floor(len / 2); i>=0; i--){
heapify(arr, i, len);
}
}
public void heapify(int[] arr, int i, int len){
int left = i * 2 + 1;
int right = i * 2 + 2;
int larger = i;
if(left < len && arr[left] > arr[larger]){
larger = left;
}
if(right < len && arr[right] > arr[larger]){
larger = right;
}
if(larger != i){
swap(arr, i, larger);
//交换之后larger位置为较小的值,继续向下调整
heapify(arr, larger, len);
}
}
}
插入排序
直接插入排序
时间复杂度O(n^2)
空间复杂度O(1)
稳定
final static class insertSort{
public insertSort(int[] arr){
Sort(arr, arr.length);
}
private void Sort(int[] arr, int n) {
for (int i = 1; i < n; i++) {
int tmp = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > tmp) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = tmp;
}
}
}
希尔排序
插入排序的改良,增加了步长
时间复杂度O(nlogn)
空间复杂度O(1)
final static class shellSort{
shellSort(int[] arr){
Sort(arr, arr.length);
}
private void Sort(int[] arr, int n) {
int gap = n;
do{
gap = gap / 3 + 1;
for (int i = gap; i < n; i++) {
int tmp = arr[i];
int j = i - gap;
while (j >= 0 && arr[j] > tmp) {
arr[j + gap] = arr[j];
j -= gap;
}
arr[j + gap] = tmp;
}
}while (gap > 1);
}
}
交换排序
冒泡排序
时间复杂度O(n^2)
空间复杂度O(1)
稳定
final static class BubbleSort{
public BubbleSort(int[] arr){
Sort(arr, arr.length);
}
private void Sort(int[] arr, int n) {
for (int i = 0; i < n; i++) {
for (int j = 1; j < n - i; j++) {
if(arr[j-1] > arr[j]){
swap(arr, j-1, j);
}
}
}
}
}
快速排序
时间复杂度O(nlogn)
最坏时间复杂度O(n^2) 当划分产生的两个子问题分别包含 n-1 和 0 个元素时,最坏情况发生。
空间复杂度O(logn) 其中sort递归调用生成partitionIndex
final static class quickSort{
public quickSort(int[] arr){
Sort(arr, 0, arr.length-1);
}
public void Sort(int[] arr, int l, int r){
if(l < r){
int partitionIndex = partition(arr, l, r);
Sort(arr, l, partitionIndex-1);
Sort(arr, partitionIndex+1, r);
}
}
public int partition(int[] arr, int l, int r){
int pivot = l;
int index = pivot + 1;
for(int i=index; i<=r; i++){
if(arr[i] < arr[pivot]){
swap(arr, i, index++);
}
}
swap(arr, pivot, index-1);
return index-1;
}
}
归并排序
时间复杂度O(nlogn)
空间复杂度O(n)
这个稍微想一下就行了,不是特别难
final static class mergeSort{
public mergeSort(int[] arr) {
Sort(arr, 0, arr.length - 1);
}
public void Sort(int[] arr, int l, int r){
if(l < r){
int mid = (l + r)/2;
Sort(arr, l, mid);
Sort(arr, mid+1, r);
merge(arr, l, mid, r);
}
}
public void merge(int[] arr, int l, int mid, int r){
int[] help = new int[r-l+1];
int count = 0;
int p = l, q = mid + 1;
while(p <= mid && q <= r){
help[count++] = arr[p] < arr[q] ? arr[p++] : arr[q++];
}
while(p <= mid){
help[count++] = arr[p++];
}
while(q <= r){
help[count++] = arr[q++];
}
for(int i = 0; i < help.length; i++){
arr[l + i] = help[i];
}
}
}
桶排序
计数排序
计数排序有点坑啊
他先找到数组中最大和最小值,然后用这个二者的差值作为计数数组的长度
如果我数组中就三个元素[1, 2, 100]就不合适了
时间复杂度O(n + k)
空间复杂度O(n + k)
final static class countSort{
countSort(int[] arr){
Sort(arr, arr.length);
}
private void Sort(int[] arr, int n) {
int max = arr[0];
int min = arr[0];
for (int i = 0; i < n; i++) {
if (max < arr[i]) {
max = arr[i];
}
if (min > arr[i]) {
min = arr[i];
}
}
// 最大最小元素之间范围[min, max]的长度
int offset = max - min + 1;
// 1. 计算频率,在需要的数组长度上额外加1
int[] count = new int[offset + 1];
for (int i = 0; i < n; i++) {
// 使用加1后的索引,有重复的该位置就自增
count[arr[i] - min + 1]++;
}
// 2. 频率 -> 元素的开始索引
for (int i = 0; i < offset; i++) {
count[i + 1] += count[i];
}
// 3. 元素按照开始索引分类,用到一个和待排数组一样大临时数组存放数据
int[] aux = new int[n];
for (int i = 0; i < n; i++) {
// 填充一个数据后,自增,以便相同的数据可以填到下一个空位
aux[count[arr[i] - min]++] = arr[i];
}
// 4. 数据回写
for (int i = 0; i < n; i++) {
arr[i] = aux[i];
}
}
}
基数排序
我复制粘贴的,不太想看了
时间复杂度O(n * m)
空间复杂度O(m)
final static class RadixSort{
public RadixSort(int[] arr) {
// 对 arr 进行拷贝,不改变参数内容
int[] array = Arrays.copyOf(arr, arr.length);
int maxDigit = getMaxDigit(array);
Sort(arr, maxDigit);
}
/**
* 获取最高位数
*/
private int getMaxDigit(int[] arr) {
int maxValue = getMaxValue(arr);
return getNumLenght(maxValue);
}
private int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
protected int getNumLenght(long num) {
if (num == 0) {
return 1;
}
int lenght = 0;
for (long temp = num; temp != 0; temp /= 10) {
lenght++;
}
return lenght;
}
private int[] Sort(int[] arr, int maxDigit) {
int mod = 10;
int dev = 1;
for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
// 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10)
int[][] counter = new int[mod * 2][0];
for (int j = 0; j < arr.length; j++) {
int bucket = ((arr[j] % mod) / dev) + mod;
counter[bucket] = arrayAppend(counter[bucket], arr[j]);
}
int pos = 0;
for (int[] bucket : counter) {
for (int value : bucket) {
arr[pos++] = value;
}
}
}
return arr;
}
/**
* 自动扩容,并保存数据
*
* @param arr
* @param value
*/
private int[] arrayAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
}
final static class mergeSort{
public mergeSort(int[] arr) {
Sort(arr, 0, arr.length - 1);
}
public void Sort(int[] arr, int l, int r){
if(l < r){
int mid = (l + r)/2;
Sort(arr, l, mid);
Sort(arr, mid+1, r);
merge(arr, l, mid, r);
}
}
public void merge(int[] arr, int l, int mid, int r){
int []help = new int[r-l+1];
int count = 0;
int p = l, q = mid + 1;
while(p<=mid && q<=r){
help[count++] = arr[p] < arr[q] ? arr[p++] : arr[q++];
}
while(p<=mid){
help[count++] = arr[p++];
}
while(q<=r){
help[count++] = arr[q++];
}
for(int i=0; i<help.length; i++){
arr[l+i] = help[i];
}
}
}