本篇博文主要记录动态规划DP这一块的学习。
印章(蓝桥杯6.27)
问题描述:共有n种图案的印章,每种图案的出现概率相同。小A买了m张印章,求小A集齐n种印章的概率。(1≤n,m≤20)
输入格式:一行两个正整数n和m
输出格式:一个实数P表示答案,保留4位小数。
思考1:
概率论?!分类讨论
1)当m<n时,集齐的概率为0
2)当m>n时,买的m张印章,每张有n种可能,分母:n的m次方;分子:(C_m^n) * (C_n m-n)(m张印章中,有n张是图案不同的,剩下的m-n张随意)。
思考2:
动态规划解题步骤:
1)设置状态,即数组
dp[i][j] = 印章数目为i、集齐j种印章的概率
dp[1][1] = 1
dp[i][1] = (1/n)^(i-1)
i < j时,dp = 0
2)确定状态转移方程
找状态之间的关系,从手里有(i-1)枚印章到 i 枚印章时,有两种情况,第一种,拿到的这枚印章种类手里已经有了,此时 dp[i][j] 表示手里已经有 j 种印章了,因此上个状态也只有 j 种印章,即 dp[i-1][j] 。dp[i][j] = dp[i-1][j] * j/n;第二种,拿到的这枚印章种类手里还没有,所以上个状态表示为dp[i-1][j-1],一共有n种印章,前面已经取了(j-1)种,而现在取的和前面没有重复,因此取的是n-(j-1)中的其中一个。
3)代码实现
n,m = map(int,input().split())
dp = [[0 for i in range(n+1)]for i in range(m+1)]
for i in range(1,m+1):
for j in range(1,n+1):
if (i < j):
dp[i][j] = 0
elif (j == 1):
dp[i][j] = (1/n)**(i-1)
else:
dp[i][j] = (dp[i-1][j])*(j*1.0/n) + (dp[i-1][j-1])*((n-j+1)*1.0/n)
print("%.4f"%(dp[m][n]))
拿金币(蓝桥杯6.28)
问题描述:有一个N x N的方格,每一个格子都有一些金币,只要站在格子里就能拿到里面的金币。你站在最左上角的格子里,每次可以从一个格子走到它右边或下边的格子里。请问如何走才能拿到最多的金币。
输入格式:第一行输入一个正整数n。以下n行描述该方格。金币数保证是不超过1000的正整数。
输出格式:最多能拿金币数量。
思考1:
n*n的方格应该用一个数组表示,dp[i][j]表示i行j列的金币数量,想要求出能拿金币最多的数量,每次移动做选择的时候,比较右边还是下边的金币数量大,哪边大就往哪边移动,直到不能移动为止(没有向右也没有向下的选择,即边界处)
思考2:
状态转移方程
dp[i][j] = max((dp[i][j-1]+dp[i][j]),(dp[i-1][j]+dp[i][j]))
代码
n = int(input())
rect = []
for i in range(n):
rect.append(list(map(int, input().split())))
#将边界的数单独算出来
for i in range(1,n):
rect[0][i] =rect[0][i] + rect[0][i-1]
for i in range(1,n):
rect[i][0] = rect[i][0] + rect[i-1][0]
for i in range(1,n):
for j in range(1,n):
rect[i][j] = max(rect[i][j-1],rect[i-1][j]) + rect[i][j]
print(rect[-1][-1])
最长回文子串(力扣6.29)

思考1:
1)关于判断是否为回文数,之前写过博客,可直接s==s[::-1]。
2)字串可通过双循环得到
3)回文字串的长度最大!?
但这种判断肯定复杂度很高,而且这道题是动态规划那一p的,所以这个思路应该不太对。
思考2:
1)s[0…j]是回文子串则s[1…j-1]必定是回文子串,而且s[0]==s[j]
2)dp[i][j]为“s[i…j]是否为回文字符串”,如果是回文字符串,则dp[i][j]=true,且dp[i][j]=dp[i+1][j-1] && s[i]==s[j](状态转移方程)
3)问题边界,有1个字符时,dp=true;有两个字符,即i+1=j时,如果s[i]==s[j],则dp[i][j]=true
代码如下:
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
if n < 2:
return s
max_len = 1
begin = 0
# dp[i][j] 表示 s[i..j] 是否是回文串
dp = [[False] * n for _ in range(n)]
for i in range(n):
dp[i][i] = True
# 递推开始
# 先枚举子串长度
for L in range(2, n + 1):
# 枚举左边界,左边界的上限设置可以宽松一些
for i in range(n):
# 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
j = L + i - 1
# 如果右边界越界,就可以退出当前循环
if j >= n:
break
if s[i] != s[j]:
dp[i][j] = False
else:
if j - i < 3:
dp[i][j] = True
else:
dp[i][j] = dp[i + 1][j - 1]
# 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if dp[i][j] and j - i + 1 > max_len:
max_len = j - i + 1
begin = i
return s[begin:begin + max_len]
最大子数组和(力扣6.30)

思考1:
dp[i][j]表示nums中从 i 到 j 位置的和。
dp[i][i]表示nums本身
状态转移方程:
i < j 时,dp[i][j] = dp[i][j-1] + nums[j]
返回dp中最大的值。
思考2:
二维数组表示最大值反而复杂了,一维数组即可。
dp[i]:表示以 nums[i] 结尾的连续子数组的最大和。
如果dp[i - 1] > 0,那么可以把nums[i]直接接在dp[i - 1]表示的那个数组的后面,得到和更大的连续子数组;
如果dp[i - 1] <= 0,那么nums[i]加上前面的数dp[i - 1]以后值不会变大。此时单独的一个nums[i]的值,就是dp[i]。
代码:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
dp = [0] * n
dp[0] = nums[0]
for i in range(1,n):
dp[i] = max(dp[i-1]+nums[i],nums[i])
return max(dp)
爬楼梯(力扣7.1)

思考1:
设置状态和边界条件:
dp[i]表示到i阶有dp[i]种方法;dp[1]=1,dp[2] = 2,dp[3]=3
状态转移方程:
dp[i] = dp[i-1] + dp[i-2]
class Solution:
def climbStairs(self, n: int) -> int:
dp = [0] * n
dp[0] = 1
ways = 0
if n == 1:
ways = 1
elif n == 2:
ways = 2
else:
dp[1] = 2
for i in range(2,n):
dp[i] = dp[i-1] + dp[i-2]
ways = dp[n-1]
return ways
杨辉三角(7.2)
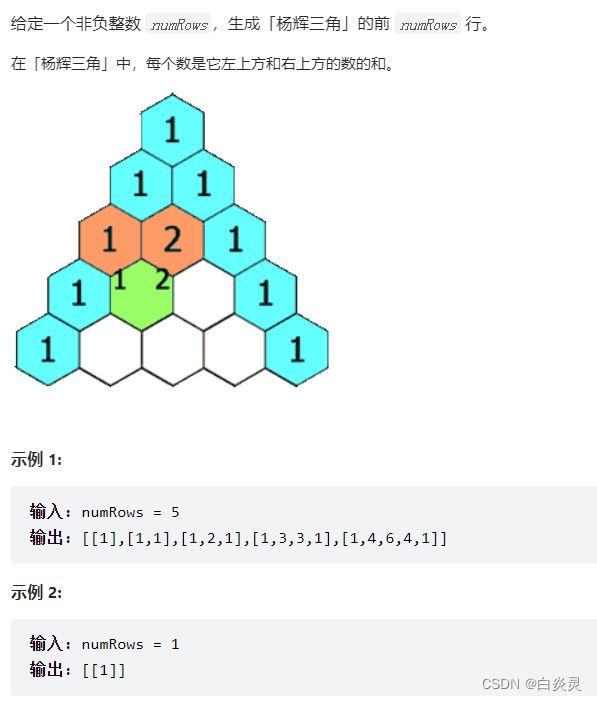
思考:
二维数组dp[i][j]表示第i行第j列的数字,每行的第一个和最后一个数字都是1。
状态转移方程:
当j=0或i时,dp[][]=1
其他情况下,dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
二维数组的创建?!
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
dp = [[0] * i for i in range(1,numRows+1)]
dp[0][0] = 1
if numRows==1:
dp = [[1]]
elif numRows==2:
dp = [[1],[1,1]]
else:
for i in range(numRows):
for j in range(i+1):
if (j==0)or(j==i):
dp[i][j] = 1
else:
dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
return dp
官方答案:
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
ret = list()
for i in range(numRows):
row = list()
for j in range(0, i + 1):
if j == 0 or j == i:
row.append(1)
else:
row.append(ret[i - 1][j] + ret[i - 1][j - 1])
ret.append(row)
return ret