本文参考国标文件GB/T 32907——2016,重点在于对示例的计算。
1范围
本标准规定了SM4分组密码算法的算法结构和算法描述,并给出了运算示例。
本标准适用于商用密码产品中分组密码算法的实现、检测和应用。
2 术语和定义
下列术语和定义适用于本文件。
2.1 分组长度 block length
一个信息分组的比特位数。
2.2 密钥长度 key length
密钥的比特位数。
2.3 密钥扩散算法 key expansion algorithm
将密钥变换为轮密钥的运算单元。
2.4 轮数 rounds
轮函数的迭代次数。
2.5 轮密钥 round key
又称子密钥,在迭代分组密码中每一轮使用的密钥,根据输入密钥用密钥编排算法推导得出。
2.6 字 word
长度为32比特的组(串)。
2.7 S盒 S-box
S盒为固定的8比特输出的置换,记为Sbox(.)。
3 符号和缩略语
下列符号和缩略语适用于本文件:
⊕ \oplus ⊕????????????????32位异或
< < < i <<<i <<<i??????32位循环左移 i i i位
Z 2 n Z_{2}^{n} Z2n??????????????长度比特为 n n n的二进制序列集合
4 算法结构
SM4密码算法是一个分组算法。该算法的分组长度为128比特,密钥长度为128比特。加密算法与密钥扩展算法均采用非线性迭代结构,运算轮数均为32轮。数据解密和数据加密的算法结构相同,只是轮密钥的使用顺序相反,解密轮密钥是加密轮密钥的逆序。
5 密钥及密钥参量
密钥长度为128比特,表示为 M K = ( M K 0 , M K 1 , M K 2 , M K 3 ) MK=(MK_0,MK_1,MK_2,MK_3) MK=(MK0?,MK1?,MK2?,MK3?),其中 M K i ( i = 0 , 1 , 2 , 3 ) MK_i(i=0,1,2,3) MKi?(i=0,1,2,3)为字。
轮密钥表示为 ( r k 0 , r k 1 , . . . , r k 31 ) (rk_0,rk_1,...,rk_{31}) (rk0?,rk1?,...,rk31?),其中 r k i ( i = 0 , . . . , 31 ) rk_i(i=0,...,31) rki?(i=0,...,31)为32比特字。轮密钥由密钥生成。
F K = ( F K 0 , F K 1 , F K 2 , F K 3 ) FK=(FK_0,FK_1,FK_2,FK_3) FK=(FK0?,FK1?,FK2?,FK3?)为系统参数, C K = ( C K 0 , C K 1 , . . . , C K 31 ) CK=(CK_0,CK_1,...,CK_{31}) CK=(CK0?,CK1?,...,CK31?)为固定参数,用于密钥扩展算法,其中 F K i ( i = 0 , . . . , 3 ) FK_i(i=0,...,3) FKi?(i=0,...,3)、 C K i ( i = 0 , . . . , 31 ) CK_i(i=0,...,31) CKi?(i=0,...,31)为字。
例:
M K = ( M K 0 , M K 1 , M K 2 , M K 3 ) = MK=(MK_0,MK_1,MK_2,MK_3)= MK=(MK0?,MK1?,MK2?,MK3?)= ( ( ( 01234567,89ABCDEF,FEDCBA98,76543210 ) ) )
r k 0 = rk_0= rk0?= F12186F9
F K = ( F K 0 , F K 1 , F K 2 , F K 3 ) = FK=(FK_0,FK_1,FK_2,FK_3)= FK=(FK0?,FK1?,FK2?,FK3?)= ( ( ( A3B1BAC6,56AA3350,677D9197,B27022DC ) ) )
C K 0 = CK_0= CK0?= 00070E15
6 轮函数 F F F
6.1 轮函数结构
设输入为 ( X 0 , X 1 , X 2 , X 3 ) ∈ ( Z 2 32 ) 4 (X_0,X_1,X_2,X_3) \in {(Z_{2}^{32})}^4 (X0?,X1?,X2?,X3?)∈(Z232?)4,轮密钥为 r k ∈ Z 2 32 rk \in Z_{2}^{32} rk∈Z232?,则轮函数 F F F见式(1):
F ( X 0 , X 1 , X 2 , X 3 , r k ) = X 0 ⊕ T ( X 1 ⊕ X 2 ⊕ X 3 ⊕ r k ) ( 1 ) F(X_0,X_1,X_2,X_3,rk)=X_0 \oplus T(X_1 \oplus X_2 \oplus X_3 \oplus rk)\quad (1) F(X0?,X1?,X2?,X3?,rk)=X0?⊕T(X1?⊕X2?⊕X3?⊕rk)(1)
例:
X 0 = X_0= X0?= 01234567
X 1 = X_1= X1?= 89ABCDEF
X 2 = X_2= X2?= FEDCBA98
X 3 = X_3= X3?= 76543210
r k 0 = rk_0= rk0?= F12186F9
X 1 ⊕ X 2 ⊕ X 3 ⊕ r k = X_1 \oplus X_2 \oplus X_3 \oplus rk= X1?⊕X2?⊕X3?⊕rk= (89ABCDEF) ⊕ \oplus ⊕ (FEDCBA98) ⊕ \oplus ⊕ (76543210) ⊕ \oplus ⊕ (F12186F9) = = = F002C39E
T ( . ) = L ( τ ( . ) ) T(.)=L(\tau (.)) T(.)=L(τ(.))
τ ( F 002 C 39 E ) = \tau(F002C39E)= τ(F002C39E)= 18E992B1
L ( B ) = B ⊕ ( B < < < 2 ) ⊕ ( B < < < 10 ) ⊕ ( B < < < 18 ) ⊕ ( B < < < 24 ) L(B)=B \oplus (B<<<2) \oplus (B<<<10) \oplus (B<<<18) \oplus (B<<<24) L(B)=B⊕(B<<<2)⊕(B<<<10)⊕(B<<<18)⊕(B<<<24)
L ( 18 E 992 B 1 ) = L(18E992B1)= L(18E992B1)= (18E992B1) ⊕ \oplus ⊕ (63A64AC4) ⊕ \oplus ⊕ (A64AC463) ⊕ \oplus ⊕ (4AC463A6) ⊕ \oplus ⊕ (B118E992) = = = 26D99622
F ( X 0 , X 1 , X 2 , X 3 , r k ) = X 0 ⊕ T ( X 1 ⊕ X 2 ⊕ X 3 ⊕ r k ) ( 1 ) = F(X_0,X_1,X_2,X_3,rk)=X_0 \oplus T(X_1 \oplus X_2 \oplus X_3 \oplus rk)\quad (1)= F(X0?,X1?,X2?,X3?,rk)=X0?⊕T(X1?⊕X2?⊕X3?⊕rk)(1)= (01234567) ⊕ \oplus ⊕ (26D99622) = = = 27FAD345
6.2 合成置换 T T T
T : Z 2 32 → Z 2 32 T:Z_{2}^{32} \to Z_{2}^{32} T:Z232?→Z232?是一个可逆变换,由非线性变换 τ \tau τ和线性变换 L L L复合而成,即 T ( . ) = L ( τ ( . ) ) T(.)=L(\tau (.)) T(.)=L(τ(.))。
a)非线性变换 τ \tau τ
τ \tau τ由4个并行的S盒构成。
设输入为 A = ( a 0 , a 1 , a 2 , a 3 ) ∈ ( Z 2 8 ) 4 A=(a_0,a_1,a_2,a_3)\in {(Z_{2}^{8})}^4 A=(a0?,a1?,a2?,a3?)∈(Z28?)4,输出为 B = ( b 0 , b 1 , b 2 , b 3 ) ∈ ( Z 2 8 ) 4 B=(b_0,b_1,b_2,b_3)\in {(Z_{2}^{8})}^4 B=(b0?,b1?,b2?,b3?)∈(Z28?)4,则见式(2):
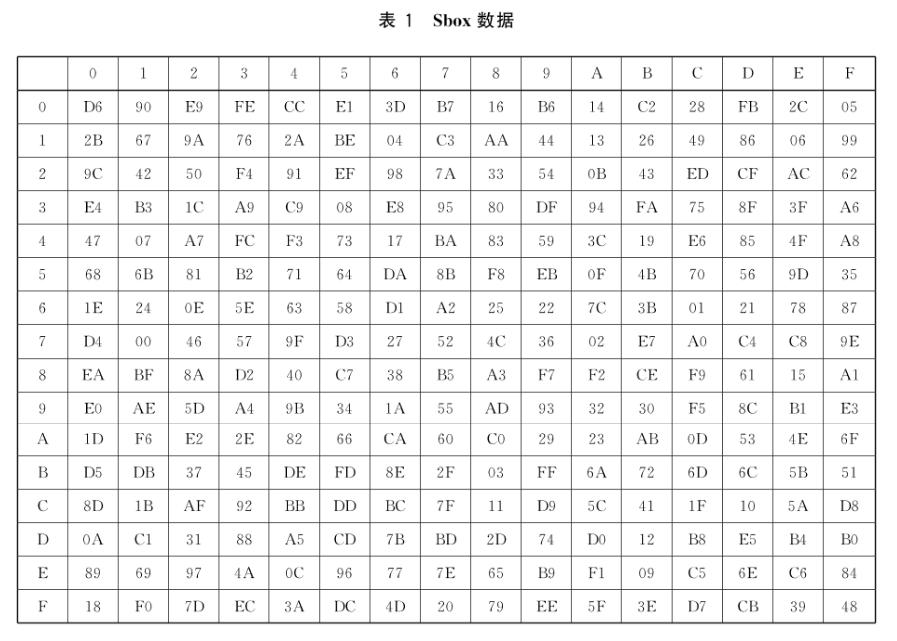
( b 0 , b 1 , b 2 , b 3 ) = τ ( A ) = ( S b o x ( a 0 ) , S b o x ( a 1 ) , S b o x ( a 2 ) , S b o x ( a 3 ) ) ( 2 ) (b_0,b_1,b_2,b_3)=\tau (A)=(Sbox(a_0),Sbox(a_1),Sbox(a_2),Sbox(a_3))\quad (2) (b0?,b1?,b2?,b3?)=τ(A)=(Sbox(a0?),Sbox(a1?),Sbox(a2?),Sbox(a3?))(2)
式中,Sbox数据见表1。
例如:输入’EF’,则经S盒后的值为表中第E行和第F列的值,Sbox(EF)=84。
b)线性变换 L L L
非线性变换 τ \tau τ的输出是线性变换 L L L的输入。设输入为 B ∈ Z 2 32 B \in Z_{2}^{32} B∈Z232?,输出为 C ∈ Z 2 32 C \in Z_{2}^{32} C∈Z232?,则见式(3):
C = L ( B ) = B ⊕ ( B < < < 2 ) ⊕ ( B < < < 10 ) ⊕ ( B < < < 18 ) ⊕ ( B < < < 24 ) ( 3 ) C=L(B)=B \oplus (B<<<2) \oplus (B<<<10) \oplus (B<<<18) \oplus (B<<<24)\quad (3) C=L(B)=B⊕(B<<<2)⊕(B<<<10)⊕(B<<<18)⊕(B<<<24)(3)
例:
B = 18 E 992 B 1 B=18E992B1 B=18E992B1
C = L ( 18 E 992 B 1 ) = C=L(18E992B1)= C=L(18E992B1)= (18E992B1) ⊕ \oplus ⊕ (63A64AC4) ⊕ \oplus ⊕ (A64AC463) ⊕ \oplus ⊕ (4AC463A6) ⊕ \oplus ⊕ (B118E992) = = = 26D99622$
7 算法描述
7.1 加密算法
本加密算法由32次迭代运算和1次反序变换 R R R组成。
设明文输入为 ( X 0 , X 1 , X 2 , X 3 ) ∈ ( Z 2 32 ) 4 (X_0,X_1,X_2,X_3) \in {(Z_{2}^{32})}^4 (X0?,X1?,X2?,X3?)∈(Z232?)4,密文输出为 ( Y 0 , Y 1 , Y 2 , Y 3 ) ∈ ( Z 2 32 ) 4 (Y_0,Y_1,Y_2,Y_3) \in {(Z_{2}^{32})}^4 (Y0?,Y1?,Y2?,Y3?)∈(Z232?)4,轮密钥为 r k i ∈ Z 2 32 , i = 0 , 1 , 2 , . . , 31 {rk}_i \in Z_{2}^{32},i=0,1,2,..,31 rki?∈Z232?,i=0,1,2,..,31。加密算法的运算过程如下:
a)32次迭代运算见式(4):
X i + 4 = F ( X i , X i + 1 , X i + 2 , X i + 3 , r k i ) , i = 0 , 1 , . . . , 31 ( 4 ) X_{i+4}=F(X_i,X_{i+1},X_{i+2},X_{i+3},{rk}_i),i=0,1,...,31 \quad (4) Xi+4?=F(Xi?,Xi+1?,Xi+2?,Xi+3?,rki?),i=0,1,...,31(4)
b)反序变换见式(5):
( Y 0 , Y 1 , Y 2 , Y 3 ) = R ( X 32 , X 33 , X 34 , X 35 ) = ( X 35 , X 34 , X 33 , X 32 ) ( 5 ) (Y_0,Y_1,Y_2,Y_3)=R(X_{32},X_{33},X_{34},X_{35})=(X_{35},X_{34},X_{33},X_{32})\quad (5) (Y0?,Y1?,Y2?,Y3?)=R(X32?,X33?,X34?,X35?)=(X35?,X34?,X33?,X32?)(5)
7.2 解密算法
本算法的解密变换与加密变换结构相同,不同的仅是轮密钥的使用顺序。解密时,使用轮密钥序 ( r k 31 , r k 30 , . . . , r k 0 ) ({rk}_{31},{rk}_{30},...,{rk}_{0}) (rk31?,rk30?,...,rk0?)。
7.3 密钥扩展算法
加密过程使用的轮密钥由加密密钥生成,其中加密密钥 M K = ( M K 0 , M K 1 , M K 2 , M K 3 ) ∈ ( Z 2 32 ) 4 MK=({MK}_0,{MK}_1,{MK}_2,{MK}_3) \in {(Z_{2}^{32})}^4 MK=(MK0?,MK1?,MK2?,MK3?)∈(Z232?)4,加密过程中的轮密钥生成方法见式(6)和式(7):
( K 0 , K 1 , K 2 , K 3 ) = ( M K 0 ⊕ F K 0 , M K 1 ⊕ F K 1 , M K 2 ⊕ F K 2 , M K 3 ⊕ F K 3 ) ( 6 ) (K_0,K_1,K_2,K_3)=({MK}_0 \oplus {FK}_0,{MK}_1 \oplus {FK}_1,{MK}_2 \oplus {FK}_2,{MK}_3 \oplus {FK}_3) \quad (6) (K0?,K1?,K2?,K3?)=(MK0?⊕FK0?,MK1?⊕FK1?,MK2?⊕FK2?,MK3?⊕FK3?)(6)
r k i = K i + 4 = K i ⊕ T ′ ( K i + 1 ⊕ K i + 2 ⊕ K i + 3 ⊕ C K i ) , i = 0 , 1 , . . . , 31 ( 7 ) {rk}_i=K_{i+4}=K_i \oplus {T}'({K_{i+1} \oplus K_{i+2} \oplus K_{i+3} \oplus {CK}_i}),i=0,1,...,31 \quad (7) rki?=Ki+4?=Ki?⊕T′(Ki+1?⊕Ki+2?⊕Ki+3?⊕CKi?),i=0,1,...,31(7)
式中:
a) T ′ {T}' T′是将6.2中合成置换 T T T的线性变换 L L L替换为 L ′ {L}' L′,见式(8):
L ′ ( B ) = B ⊕ ( B < < < 13 ) ⊕ ( B < < < 23 ) ( 8 ) {L}'(B)=B \oplus (B<<<13) \oplus (B<<<23) \quad (8) L′(B)=B⊕(B<<<13)⊕(B<<<23)(8)
b)系统参数 F K FK FK的取值为:
F K 0 = ( A 3 B 1 B A C 6 ) , F K 1 = ( 56 A A 3350 ) , F K 2 = ( 677 D 9197 ) , F K 3 = ( B 27022 D C ) {FK}_0=(A3B1BAC6),{FK}_1=(56AA3350),{FK}_2=(677D9197),{FK}_3=(B27022DC) FK0?=(A3B1BAC6),FK1?=(56AA3350),FK2?=(677D9197),FK3?=(B27022DC)
c)固定参数 C K CK CK取值方法为:
设 c k i , j ck_{i,j} cki,j?为 C K i CK_{i} CKi?的第 j j j字节 ( i = 0 , 1 , . . . , 31 ; j = 0 , 1 , 2 , 3 ) (i=0,1,...,31;j=0,1,2,3) (i=0,1,...,31;j=0,1,2,3),即 C K i = ( c k i , 0 , c k i , 1 , c k i , 2 , c k i , 3 ) ∈ ( Z 2 8 ) 4 CK_{i}=(ck_{i,0},ck_{i,1},ck_{i,2},ck_{i,3}) \in {(Z_{2}^{8})}^4 CKi?=(cki,0?,cki,1?,cki,2?,cki,3?)∈(Z28?)4,则 c k i , j = ( 4 i + j ) × 7 ( m o d 256 ) ck_{i,j}=(4i+j) \times 7(mod \quad 256) cki,j?=(4i+j)×7(mod256)。
固定参数 C K i ( i = 0 , 1 , . . . , 31 ) {CK}_i(i=0,1,...,31) CKi?(i=0,1,...,31)具体值为:
解密密钥同加密密钥,解密使用的轮密钥由解密密钥生成,其轮密钥生成方法同加密过程的轮密钥生成方法。
例:
M K = ( M K 0 , M K 1 , M K 2 , M K 3 ) = MK=({MK_0},{MK_1},{MK_2},{MK_3})= MK=(MK0?,MK1?,MK2?,MK3?)= (01234567,89ABCDEF,FEDCBA98,76543210)
K 0 = M K 0 ⊕ F K 0 = K_0={MK}_0 \oplus {FK}_0= K0?=MK0?⊕FK0?=(01234567) ⊕ \oplus ⊕ (A3B1BAC6) = = = A292FFA1
K 1 = M K 1 ⊕ F K 1 = K_1={MK}_1 \oplus {FK}_1= K1?=MK1?⊕FK1?=(89ABCDEF) ⊕ \oplus ⊕ (56AA3350) = = = DF01FEBF
K 2 = M K 2 ⊕ F K 2 = K_2={MK}_2 \oplus {FK}_2= K2?=MK2?⊕FK2?=(FEDCBA98) ⊕ \oplus ⊕ (677D9197) = = = 99A12B0F
K 3 = M K 3 ⊕ F K 3 = K_3={MK}_3 \oplus {FK}_3= K3?=MK3?⊕FK3?=(76543210) ⊕ \oplus ⊕ (B27022DC) = = = C42410CC
r k 0 = K 4 = K 0 ⊕ T ′ ( K 1 ⊕ K 2 ⊕ K 3 ⊕ C K 0 ) {rk}_0=K_4=K_0 \oplus {T}'({K_1 \oplus K_2 \oplus K_3 \oplus {CK}_0}) rk0?=K4?=K0?⊕T′(K1?⊕K2?⊕K3?⊕CK0?)
K 1 ⊕ K 2 ⊕ K 3 ⊕ C K 0 = K_1 \oplus K_2 \oplus K_3 \oplus {CK}_0= K1?⊕K2?⊕K3?⊕CK0?= (DF01FEBF) ⊕ \oplus ⊕ (99A12B0F) ⊕ \oplus ⊕ (C42410CC) ⊕ \oplus ⊕ (00070E15) = = = 8283CB69
τ ( 8283 C B 69 ) = \tau(8283CB69)= τ(8283CB69)= 8AD24122
T ′ ( 8283 C B 69 ) = L ′ ( 8 A D 24122 ) = {T}'(8283CB69)={L}'(8AD24122)= T′(8283CB69)=L′(8AD24122)= (8AD24122) ⊕ \oplus ⊕ (4824515A) ⊕ \oplus ⊕ (91456920) = = = 53B37958
r k 0 = K 4 = K 0 ⊕ T ′ ( K 1 ⊕ K 2 ⊕ K 3 ⊕ C K 0 ) = {rk}_0=K_4=K_0 \oplus {T}'({K_1 \oplus K_2 \oplus K_3 \oplus {CK}_0})= rk0?=K4?=K0?⊕T′(K1?⊕K2?⊕K3?⊕CK0?)= (A292FFA1) ⊕ \oplus ⊕ 53B37958 = = = F12186F9
8 完整代码
//sm4.h
#ifndef _SM4_H_
#define _SM4_H_
#include<stdio.h>
const char Sbox[16][16]={{0xD6,0x90,0xE9,0xFE,0xCC,0xE1,0x3D,0xB7,0x16,0xB6,0x14,0xC2,0x28,0xFB,0x2C,0x05},
{0x2B,0x67,0x9A,0x76,0x2A,0xBE,0x04,0xC3,0xAA,0x44,0x13,0x26,0x49,0x86,0x06,0x99},
{0x9C,0x42,0x50,0xF4,0x91,0xEF,0x98,0x7A,0x33,0x54,0x0B,0x43,0xED,0xCF,0xAC,0x62},
{0xE4,0xB3,0x1C,0xA9,0xC9,0x08,0xE8,0x95,0x80,0xDF,0x94,0xFA,0x75,0x8F,0x3F,0xA6},
{0x47,0x07,0xA7,0xFC,0xF3,0x73,0x17,0xBA,0x83,0x59,0x3C,0x19,0xE6,0x85,0x4F,0xA8},
{0x68,0x6B,0x81,0xB2,0x71,0x64,0xDA,0x8B,0xF8,0xEB,0x0F,0x4B,0x70,0x56,0x9D,0x35},
{0x1E,0x24,0x0E,0x5E,0x63,0x58,0xD1,0xA2,0x25,0x22,0x7C,0x3B,0x01,0x21,0x78,0x87},
{0xD4,0x00,0x46,0x57,0x9F,0xD3,0x27,0x52,0x4C,0x36,0x02,0xE7,0xA0,0xC4,0xC8,0x9E},
{0xEA,0xBF,0x8A,0xD2,0x40,0xC7,0x38,0xB5,0xA3,0xF7,0xF2,0xCE,0xF9,0x61,0x15,0xA1},
{0xE0,0xAE,0x5D,0xA4,0x9B,0x34,0x1A,0x55,0xAD,0x93,0x32,0x30,0xF5,0x8C,0xB1,0xE3},
{0x1D,0xF6,0xE2,0x2E,0x82,0x66,0xCA,0x60,0xC0,0x29,0x23,0xAB,0x0D,0x53,0x4E,0x6F},
{0xD5,0xDB,0x37,0x45,0xDE,0xFD,0x8E,0x2F,0x03,0xFF,0x6A,0x72,0x6D,0x6C,0x5B,0x51},
{0x8D,0x1B,0xAF,0x92,0xBB,0xDD,0xBC,0x7F,0x11,0xD9,0x5C,0x41,0x1F,0x10,0x5A,0xD8},
{0x0A,0xC1,0x31,0x88,0xA5,0xCD,0x7B,0xBD,0x2D,0x74,0xD0,0x12,0xB8,0xE5,0xB4,0xB0},
{0x89,0x69,0x97,0x4A,0x0C,0x96,0x77,0x7E,0x65,0xB9,0xF1,0x09,0xC5,0x6E,0xC6,0x84},
{0x18,0xF0,0x7D,0xEC,0x3A,0xDC,0x4D,0x20,0x79,0xEE,0x5F,0x3E,0xD7,0xCB,0x39,0x48}
};
const int CK_Param[32] = {0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279};
const int FK_Param[4] = {0xA3B1BAC6,0x56AA3350,0x677D9197,0xB27022DC};
#endif
//sm4.c
#include "sm4.h"
unsigned int SboxFunc(unsigned int data);//S盒替换操作
unsigned int move(unsigned int data,int length);//循环移位操作
unsigned int LinearTransformation(unsigned int data);//线性变换L
unsigned int LinesarTransformation2(unsigned int data);//线性变换L'
unsigned int CompositionSubstitution(unsigned int data);//合成置换T
unsigned int CompositionSubstitution2(unsigned int data);//合成置换T'
unsigned int RoundFunction(unsigned int X0,unsigned int X1,unsigned int X2,unsigned int X3,unsigned int rk);//轮函数
unsigned int *RoundKeyExpansion(unsigned int MK0,unsigned int MK1,unsigned int MK2,unsigned int MK3);
void Encrypt(unsigned int plaintext[],unsigned int key[]);//加密
void Decrypt(unsigned int ciphertext[],unsigned int key[]);//解密
unsigned int SboxFunc(unsigned int data)
{
unsigned int result = 0;
unsigned char temp = data>>(24);
unsigned char row = (temp>>4)&0x0f;
unsigned char column = temp&0x0f;
unsigned int value = Sbox[row][column]<<(24)&0xff000000;
result = result^value;
temp = data>>(16);
row = (temp>>4)&0x0f;
column = temp&0x0f;
value = Sbox[row][column]<<(16)&0x00ff0000;
result = result^value;
temp = data>>(8);
row = (temp>>4)&0x0f;
column = temp&0x0f;
value = Sbox[row][column]<<(8)&0x0000ff00;
result = result^value;
temp = data;
row = (temp>>4)&0x0f;
column = temp&0x0f;
value = Sbox[row][column]&0x000000ff;
result = result^value;
return result;
}
unsigned int move(unsigned int data , int length)
{
unsigned int result = 0;
result = (data << length) ^ (data >> (32-length));
return result;
}
unsigned int LinearTransformation(unsigned int data)
{
unsigned int result = 0;
result = data ^ move(data,2) ^ move(data,10) ^ move(data,18) ^ move(data,24);
return result;
}
unsigned int LinesarTransformation2(unsigned int data)
{
unsigned int result = 0;
result = data^move(data,13)^move(data,23);
return result;
}
unsigned int CompositionSubstitution(unsigned int data)
{
unsigned int result = 0;
result = LinearTransformation(SboxFunc(data));
return result;
}
unsigned int CompositionSubstitution2(unsigned int data)
{
unsigned int result = 0;
result = LinesarTransformation2(SboxFunc(data));
return result;
}
unsigned int RoundFunction(unsigned int X0,unsigned int X1,unsigned int X2,unsigned int X3,unsigned int rk)
{
unsigned int result = 0;
result = X0^CompositionSubstitution(X1^X2^X3^rk);
return result;
}
unsigned int * RoundKeyExpansion(unsigned int MK0,unsigned int MK1,unsigned int MK2,unsigned int MK3)
{
unsigned static int rk[32] = {0};
unsigned int K[36] = {0};
K[0] = MK0^FK_Param[0];
K[1] = MK1^FK_Param[1];
K[2] = MK2^FK_Param[2];
K[3] = MK3^FK_Param[3];
for(int i=0;i<32;i++)
{
K[i+4] = K[i]^CompositionSubstitution2(K[i+1]^K[i+2]^K[i+3]^CK_Param[i]);
rk[i]=K[i+4];
}
return rk;
}
void Encrypt(unsigned int plaintext[],unsigned int key[])
{
unsigned int *rk = RoundKeyExpansion(key[0],key[1],key[2],key[3]);
unsigned int X[36] = {0};
for(int i=0;i<4;i++)
X[i] = plaintext[i];
for(int i=0;i<32;i++)
{
X[i+4] = RoundFunction(X[i],X[i+1],X[i+2],X[i+3],*(rk+i));
}
printf("明文为:0x%.8x 0x%.8x 0x%.8x 0x%.8x\n",plaintext[0],plaintext[1],plaintext[2],plaintext[3]);
printf("密钥为:0x%.8x 0x%.8x 0x%.8x 0x%.8x\n",key[0],key[1],key[2],key[3]);
printf("加密结果为:0x%.8x 0x%.8x 0x%.8x 0x%.8x\n",X[35],X[34],X[33],X[32]);
}
void Decrypt(unsigned int ciphertext[],unsigned int key[])
{
unsigned int *rk = RoundKeyExpansion(key[0],key[1],key[2],key[3]);
unsigned int X[36] = {0};
for(int i=0;i<4;i++)
X[i] = ciphertext[i];
for(int i=0;i<32;i++)
{
X[i+4] = RoundFunction(X[i],X[i+1],X[i+2],X[i+3],*(rk+(31-i)));
}
printf("密文为:0x%.8x 0x%.8x 0x%.8x 0x%.8x\n",ciphertext[0],ciphertext[1],ciphertext[2],ciphertext[3]);
printf("密钥为:0x%.8x 0x%.8x 0x%.8x 0x%.8x\n",key[0],key[1],key[2],key[3]);
printf("解密结果为:0x%.8x 0x%.8x 0x%.8x 0x%.8x\n",X[35],X[34],X[33],X[32]);
}
int main()
{
unsigned int plaintext[4] = {0x01234567,0x89ABCDEF,0xFEDCBA98,0x76543210};
unsigned int ciphertext[4] = {0x681edf34,0xd206965e,0x86b3e94f,0x536e4246};
unsigned int key[4] = {0x01234567,0x89ABCDEF,0xFEDCBA98,0x76543210};
// Encrypt(plaintext,key);
Decrypt(ciphertext,key);
return 0;
}