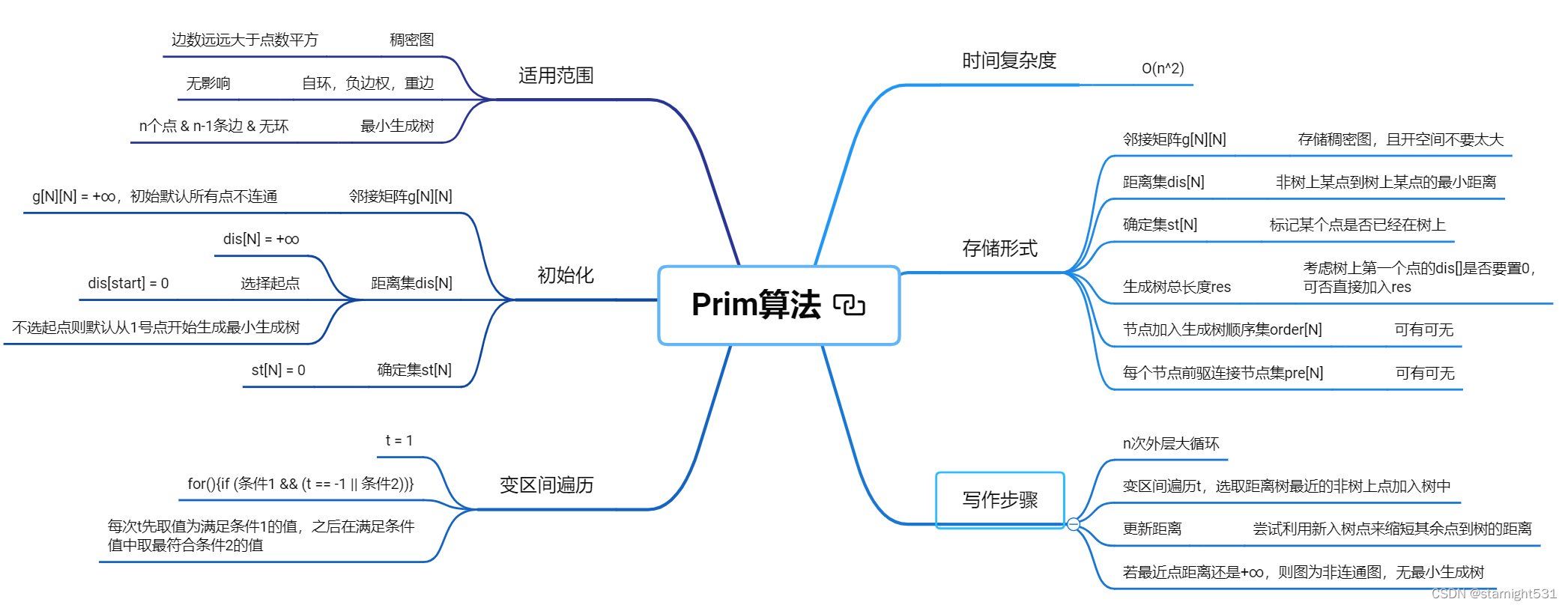
Prim
食用指南:
对该算法程序编写以及踩坑点很熟悉的同学可以直接跳转到代码模板查看完整代码
只有基础算法的题目会有关于该算法的原理,实现步骤,代码注意点,代码模板,代码误区的讲解
非基础算法的题目侧重题目分析,代码实现,以及必要的代码理解误区
题目描述:
-
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 E 中 n?1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。数据范围
1≤n≤500,
1≤m≤105,
图中涉及边的边权的绝对值均不超过 10000。输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6 -
题目来源:https://www.acwing.com/problem/content/860/
题目分析:
- 图论,点数n<500,边数m<105,m > n2,稠密无向图
- 最小生成树:寻求n-1条边将n个点连接起来,且边权和最小,树为无环连通图
- 含有重边:每次挑选一组重边中最短的一条
- 含有自环:生成树的产生过程为选择从一点到另一点的最短边,不存在自己选择自己情况
- 含有负边权:单纯边还是挑选最短者,若形成负环也不影响生成树的选择
- 针对最小生成树问题,有专门两种算法:从点出发O(n2)的Prim 和 从边出发O(mlogm)的Kruskal
- 下面我们来看看为什么Prim算法为O(n2),以及它和求单源非负边权最短距离的Dijkstra算法的相似点
算法原理:
模板算法:
- 传送门:邻接表/邻接矩阵
- 传送门: 朴素Dijkstra
- 传送门:堆优化Dijkstra
Prim算法:
1. 适用情况:
- 稠密图,当边数m >> 点数n时,O(n2)必然块于O(mlogm)
- 重边,负边权,自环,他环,均对最小生成树无影响
2. 存储形式:
- 确定集st[N]:一点x若已被加入最小生成树,则st[x] = 1
- 距离集dis[N]:与Dijkstra不同,此处的dis[x]为节点x到最小生成树的最近距离,至于是到最小生成树中哪一点则不关注
- 稠密图:邻接矩阵g[N][N]存储,由于有重边,所以输入时,g[x][y]选择xy两点中最短的边记录
- res:记录最小生成树的总长度,至于采用long long类型 或是 int类型,看题意
3. 初始化:
- 距离集dis[N]:
法一:将目标起点start的dis[start]=0,其余点的dis[]设置为+∞
法二:所有点的dis[]均是+∞,包括目标起点。之后每次默认从1号点开始生成最小生成树 - 确定集st[N]:
所有点的st[N]都初始化为0,之后每次选择距离最小生成树最近的点x加入最小生成树,将其st[x]=1
针对dis[]法一,第一个加入确定集的点就是dis[]=0的点
针对dis[]法二,第一个加入确定集的点是1号点 - 邻接矩阵g[N][N]:初始假设每个点都不连通,g[i][j]都是+∞
4. 三大步骤:
- 遍历所有不在最小生成树上的点,选择距离最小生成树dis[]最近的点x加入最小生成树
- 加入后更新与x连通的其他点到生成树的距离dis[]
- 由于每次只向最小生成树中加入了一个点,所以需要循环上述两步n次
- 时间复杂度:
外层大循环n次,
最坏需要遍历n个点在内层选取距离树最近的非树上点,
之后更新与新加点连接点到树的距离也需要遍历n次,
最坏时间复杂度O(2n2)
实际效果应该小于O(n2)
5. 模拟过程:
- 生成下面图的最小生成树:
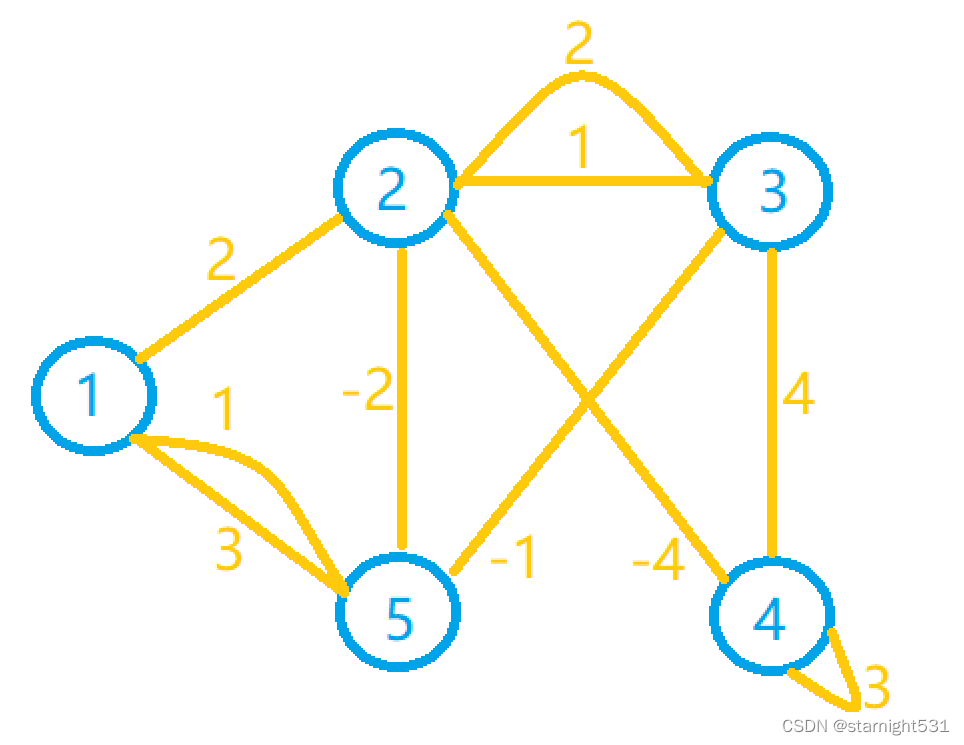
- 5个点必然需要循环5次,每次选择距离树最近的非树点x加入树,加入后尝试利用x缩短其余点到树的距离
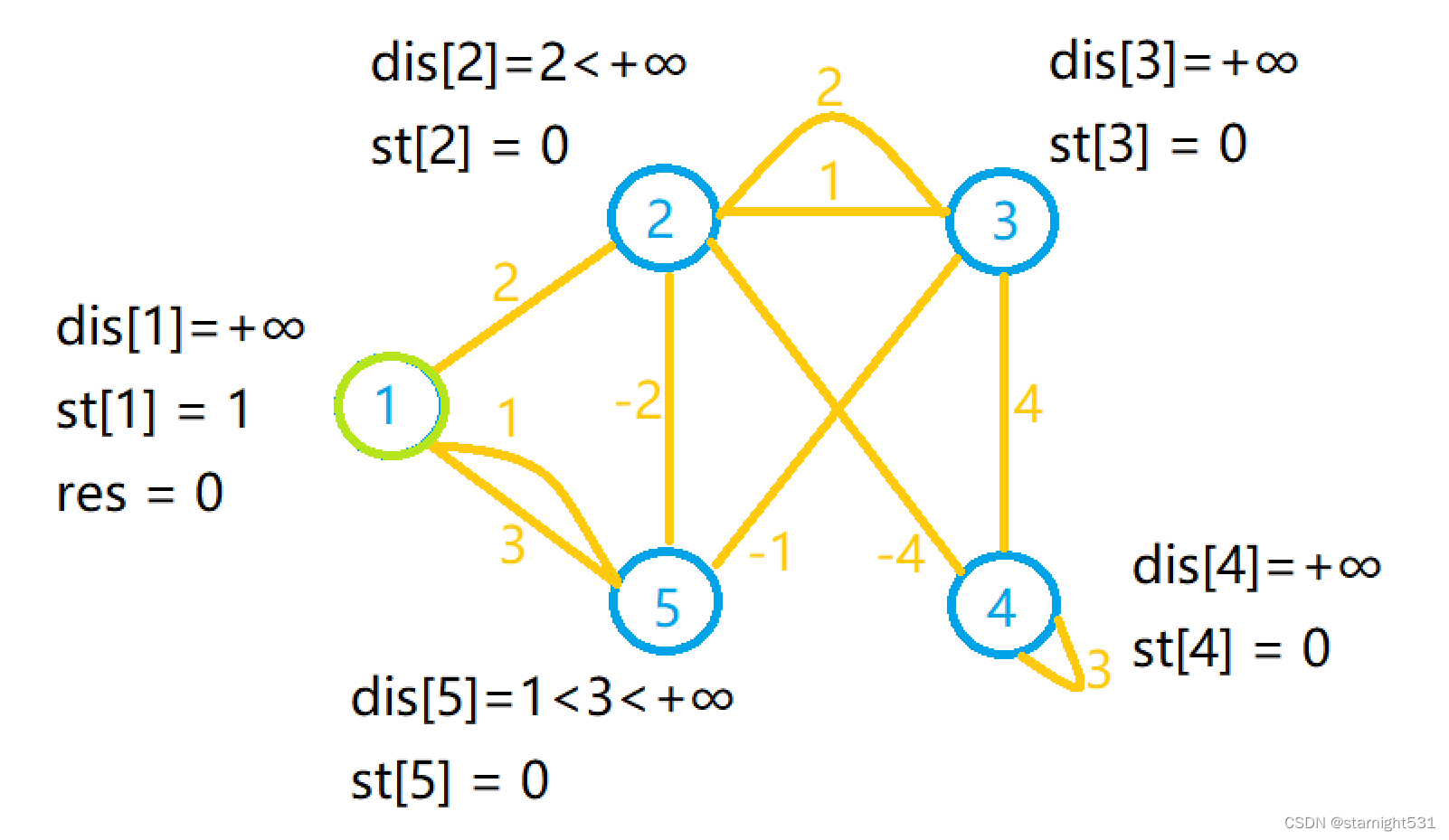
- 第一次循环:选择1作为生成树起点,顺便更新dis[2]和dis[5]
- 第二次循环:由长度为1的边选择5作为下一点,顺便更新dis[2]和dis[3]
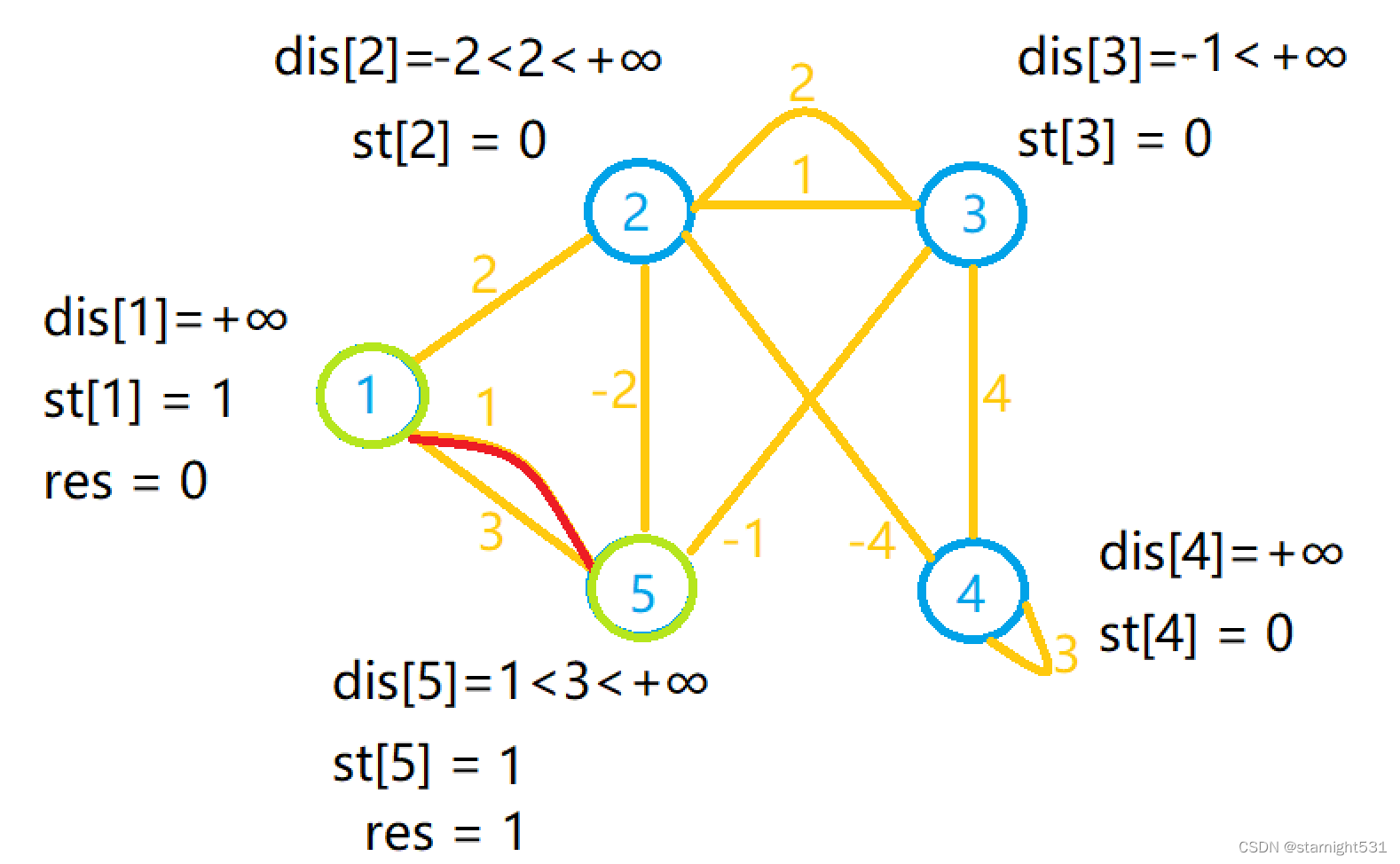
- 第三次循环:由长度为-2的边选择2作为下一点,顺便更新dis[4]
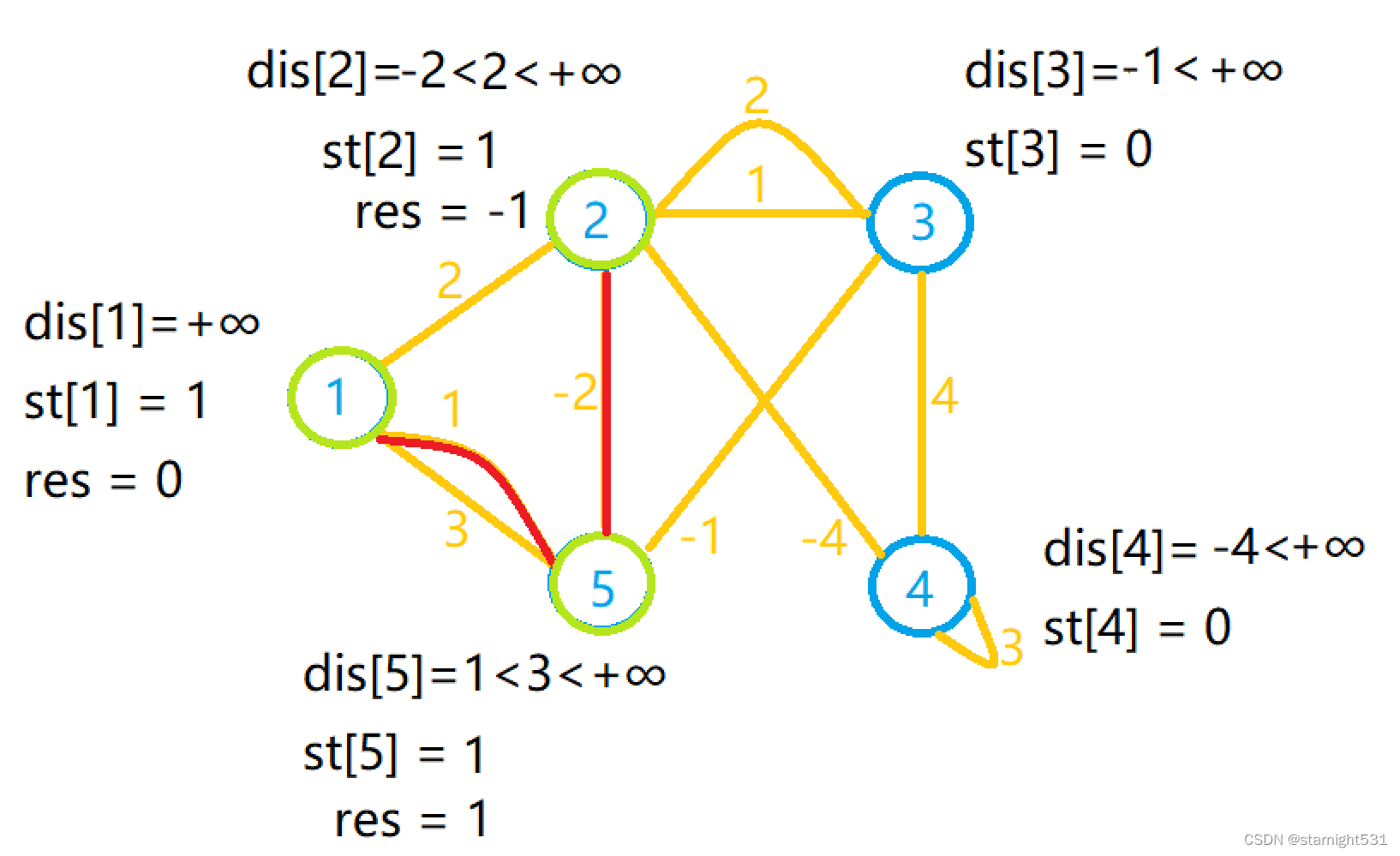
- 第四次循环:由长度为-4的边选择4作为下一点,没有可以更新点
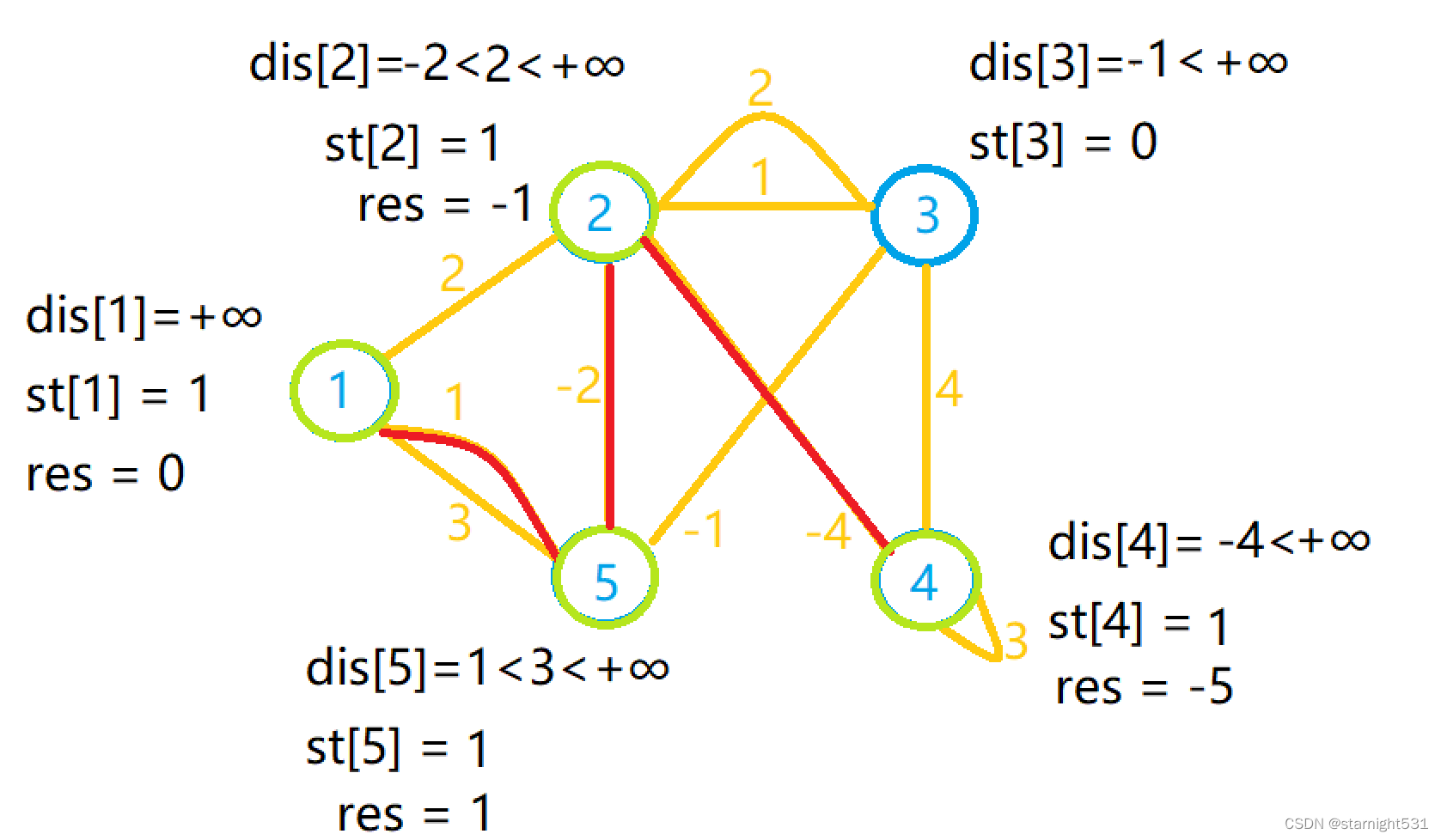
- 第五次循环:由长度为-1的边选择3作为下一点,没有可以更新点
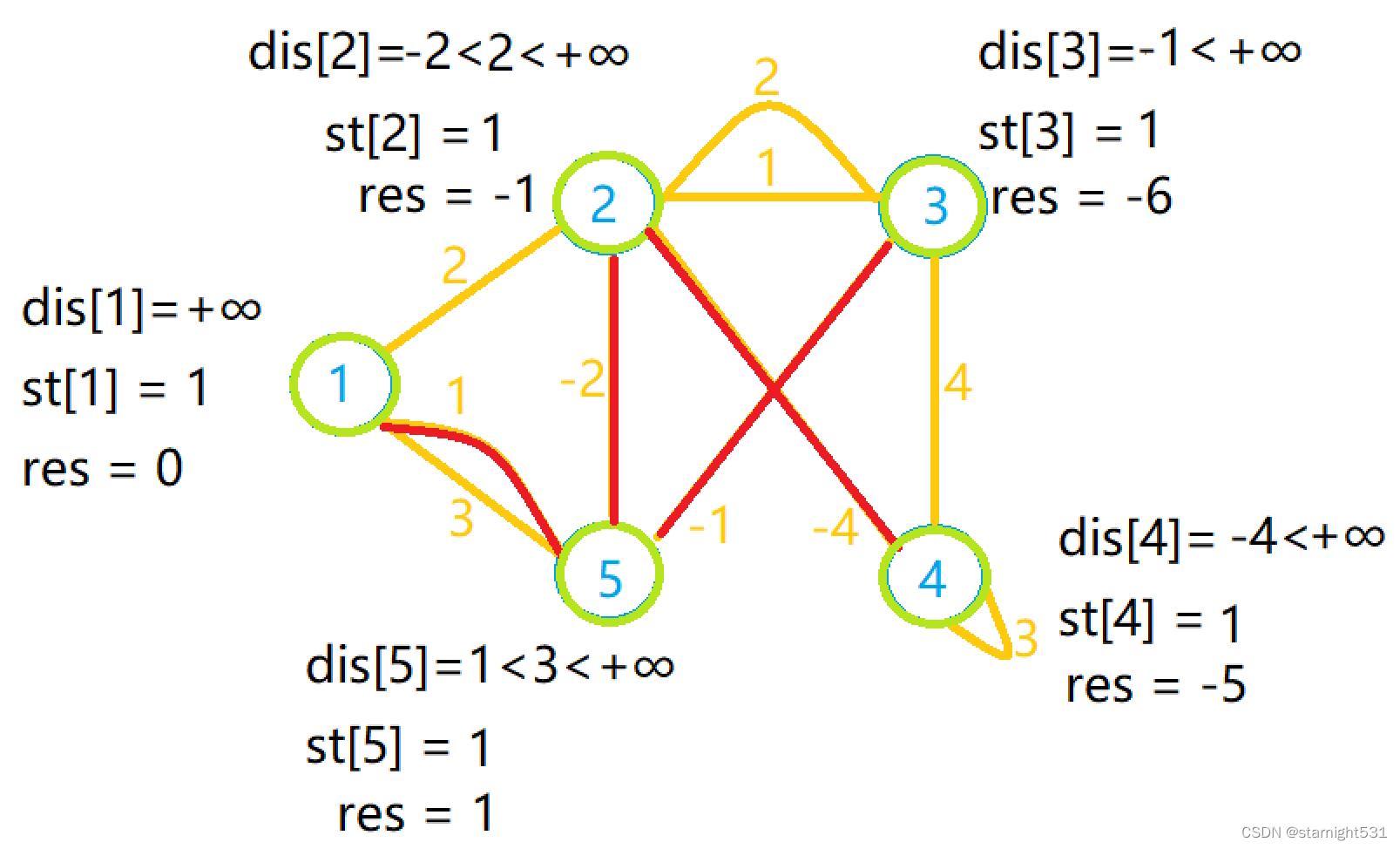
写作步骤:
1. 外层大循环:
- 每次新加入最小生成树仅一个点,共需要外层大循环n次后,所有点才都加入到了最小生成树
2. 选择最近点:
- 遍历所有st[x]==0,未加入最小生成树的点,将到最小生成树dis[]最近的点x,加入最小生成树中
- 若此时距离最小生成树最近点的距离是+∞,则说明图是非连通图,不存在所有点的最小生成树
3. 更新连接点:
- 每次选择一点x加入到最小生成树后,遍历其余所有点,尝试利用x将其他点到最小生成树的距离dis[]缩短
代码实现:
默认选择1号点作为树的起点:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f;
int g[N][N];
int dis[N];
bool st[N];
int n, m;
int prim(){
memset(dis, 0x3f, sizeof dis);
int res = 0;
//注意点1:外层n次大循环
for (int i=0; i<n; i++){
int t = -1; //t用于确定最近点下标
//注意点2:选择最近非树上点
for (int j=1; j<=n; j++){
if (!st[j] && (t == -1 || dis[j] < dis[t])){
t = j; //若是第一次选择树上点,则t==-1,接着选择j==1号点。若不是第一次择点,择t!=-1,由距离集dis[]最小者确定最近非树上点
}
}
if (i && dis[t] == INF) return INF;
if (i) res += dis[t];
st[t] = 1;
//注意点3:利用新入树点更新其余点到树的距离
for(int j=1; j<=n; j++){
dis[j] = min(dis[j], g[t][j]);
}
}
return res;
}
int main(){
memset(g, 0x3f, sizeof g);
cin >>n >>m;
for(int i=0; i<m; i++){
int a=0, b=0, c=0;
cin >>a >>b >>c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
int t = prim();
if (t == INF) cout<<"impossible" <<endl;
else cout << t <<endl;
return 0;
}
指定一点作为树的起点:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f;
int g[N][N];
int dis[N];
bool st[N];
int n, m;
int prim(int start){
memset(dis, 0x3f, sizeof dis);
dis[start] = 0;
int res = 0;
//注意点1:外层n次大循环
for (int i=0; i<n; i++){
int t = -1; //t用于确定最近点下标
//注意点2:选择最近非树上点
for (int j=1; j<=n; j++){
if (!st[j] && (t == -1 || dis[j] < dis[t])){
t = j; //若是第一次选择树上点,则t==-1,接着选择最近点x即dis[x]==0。若不是第一次择点,择t!=-1,由距离集dis[]最小者确定最近非树上点
}
}
if (i && dis[t] == INF) return INF;
res += dis[t]; //第一个点dis[]==0,可以直接加入res,不必判断是否是第一个加入树的点了
st[t] = 1;
//注意点3:利用新入树点更新其余点到树的距离
for(int j=1; j<=n; j++){
dis[j] = min(dis[j], g[t][j]);
}
}
return res;
}
int main(){
memset(g, 0x3f, sizeof g);
cin >>n >>m;
for(int i=0; i<m; i++){
int a=0, b=0, c=0;
cin >>a >>b >>c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
int t = prim(1); //某些图仅含1点
if (t == INF) cout<<"impossible" <<endl;
else cout << t <<endl;
return 0;
}
记录生成树的路径:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f;
int g[N][N];
int dis[N];
bool st[N];
int pre[N]; //前驱节点记录
int rode[N]; //依次记录先后加入树的节点
int idx;
int n, m;
int prim(int start){
memset(dis, 0x3f, sizeof dis);
dis[start] = 0;
int res = 0;
//注意点1:外层n次大循环
for (int i=0; i<n; i++){
int t = -1; //t用于确定最近点下标
//注意点2:选择最近非树上点
for (int j=1; j<=n; j++){
if (!st[j] && (t == -1 || dis[j] < dis[t])){
t = j; //若是第一次选择树上点,则t==-1,接着选择j==1号点。若不是第一次择点,择t!=-1,由距离集dis[]最小者确定最近非树上点
}
}
rode[idx++] = t;
if (i && dis[t] == INF) return INF;
if (i) res += dis[t];
st[t] = 1;
//注意点3:利用新入树点更新其余点到树的距离
for(int j=1; j<=n; j++){
if (!st[j] && dis[j]>g[t][j]){
dis[j] = g[t][j];
pre[j] = t;
}
}
}
return res;
}
void showtree(){
for(int i=0; i<idx; i++){
cout<<"第"<<i+1<<"个加入树的节点是"<<rode[i] <<"其前缀节点是"<<pre[rode[i]]<<endl;
}
}
int main(){
memset(g, 0x3f, sizeof g);
cin >>n >>m;
for(int i=0; i<m; i++){
int a=0, b=0, c=0;
cin >>a >>b >>c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
int t = prim(1);
if (t == INF) cout<<"impossible" <<endl;
else cout << t <<endl;
showtree();
return 0;
}
代码误区:
1. 变区域遍历算法:
- 在步骤二中,我们需要每次从非树上点中选择距离树最近的一点加入树,
而每次条件1非树上点的范围在改变,导致每次条件2距离树最近的点也在改变 - 对于变化区域中选择符合条件点的情况,遍历的难点在于新区域的起始点不确定
我们可以使用固定的下列代码进行选择起点后遍历:
int t = -1;
for(int i=0; i<n; i++){
if (条件1 && (t ==-1 || 条件2)) //可以继续加&&条件3,||条件4……
t = i;
}
-
条件1的作用是缩小选择范围
条件2的作用是在范围中选择最符合目标的值t的第一个值为-1
第二个值为0~n中满足条件1的值
第三个及以后的值为0~n中满足条件1和条件2的值
最终值为0~n中满足条件1和最符合条件2的值
2. 指定起点开始生成树和默认1号开始生成树的区别:
-
由于本题图中点数最少为一个,又要保证生成树的第一个点存在于图中
所以和默认1号点开始一样,指定起点也是从1号点开始加入最小生成树。 -
唯一的区别在于最终最小生成树总距离res的累加:
默认1号开始生成树,dis[1]初始为+∞,在加入res时候需要区分是否是第一个点
指定起点开始生成树,dis[start]初始为0,在加入res时不需要区分是否是第一个点
-
本题用不着指定起点开始生成最小生成树,但是其余题目可能用到。
3. 易忘点:
- 三个初始化:
初始化dis[N]为无穷
初始化g[N][N]为无穷
初始化st[N]为0 - 计算生成树总长度时,考虑是否要区分第一个加入树的点
- 非连通图情况:
每次确定距离树最近的非树上点x后,要查看其dis[x]是否+∞,若为+∞则非连通图不存在最小生成树
本篇感想:
- 24号考完期末,之后6天玩了一天,昨天写完所有大作业,假期正式开始
距离上一篇神机百炼-Ford更新已经过去37天,5周时间。
好久不写博客有点生疏了,感觉这篇干货还是有点湿 - 看完本篇博客,恭喜已登 《筑基境-后期》

距离登仙境不远了,加油 