二叉树
typedef int KEY_VALUE;
#define BSTREE_ENTRY(name, type) \
struct name { \
struct type *left; \
struct type *right; \
}
struct bstree_node {
KEY_VALUE data;
BSTREE_ENTRY(, bstree_node) bst;
};
struct bstree {
struct bstree_node *root;
};
struct bstree_node *bstree_create_node(KEY_VALUE key) {
struct bstree_node *node = (struct bstree_node*)malloc(sizeof(struct bstree_node));
if (node == NULL) {
assert(0);
}
node->data = key;
node->bst.left = node->bst.right = NULL;
return node;
}
int bstree_insert(struct bstree *T, int key) {
assert(T != NULL);
if (T->root == NULL) {
T->root = bstree_create_node(key);
return 0;
}
struct bstree_node *node = T->root;
struct bstree_node *tmp = T->root;
while (node != NULL) {
tmp = node;
if (key < node->data) {
node = node->bst.left;
} else {
node = node->bst.right;
}
}
if (key < tmp->data) {
tmp->bst.left = bstree_create_node(key);
} else {
tmp->bst.right = bstree_create_node(key);
}
return 0;
}
int bstree_traversal(struct bstree_node *node) {
if (node == NULL) return 0;
bstree_traversal(node->bst.left);
printf("%4d ", node->data);
bstree_traversal(node->bst.right);
}
#define ARRAY_LENGTH 20
int main() {
int keyArray[ARRAY_LENGTH] = {24,25,13,35,23, 26,67,47,38,98, 20,13,17,49,12, 21,9,18,14,15};
struct bstree T = {0};
int i = 0;
for (i = 0;i < ARRAY_LENGTH;i ++) {
bstree_insert(&T, keyArray[i]);
}
bstree_traversal(T.root);
printf("\n");
}
struct sched
{
BSTREE_ENTRY(, bstree_node) ready;
BSTREE_ENTRY(, bstree_node) defer;
BSTREE_ENTRY(, bstree_node) sleep;
BSTREE_ENTRY(, bstree_node) wait;
}
#endif
红黑树
\1. 每个结点是红的或者黑的
\2. 根结点是黑的
\3. 每个叶子结点是黑的
\4. 如果一个结点是红的,则它的两个儿子都是黑的
\5. 对每个结点,从该结点到其子孙结点的所有路径上的包含相同数目的黑结点
节点结构
相比二叉树红黑树多了parent节点,红黑树涉及很多旋转操作需要父节点
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define RED 1
#define BLACK 2
typedef int KEY_TYPE;
typedef struct _rbtree_node {
unsigned char color;
struct _rbtree_node *right;
struct _rbtree_node *left;
struct _rbtree_node *parent; //和二叉树的不同点
KEY_TYPE key;
void *value;
} rbtree_node;
typedef struct _rbtree {
rbtree_node *root;
rbtree_node *nil;
} rbtree;
左旋和右旋
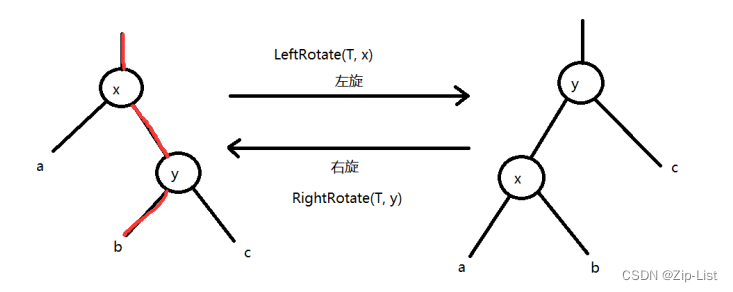
改变6个指针的指向
void rbtree_left_rotate(rbtree *T, rbtree_node *x) {
//总共改变6个指针的指向
rbtree_node *y = x->right; // x --> y , y --> x, right --> left, left --> right
x->right = y->left; //1 1
if (y->left != T->nil) { //1 2
y->left->parent = x;
}
y->parent = x->parent; //1 3
if (x->parent == T->nil) { //1 4 //x是root节点
T->root = y;
} else if (x == x->parent->left) { //判断x是父节点的左子树还是右子树
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x; //1 5
x->parent = y; //1 6
}
//右旋 在 左旋的基础上 x/y互换 left/right互换
void rbtree_right_rotate(rbtree *T, rbtree_node *y) {
rbtree_node *x = y->left;
y->left = x->right;
if (x->right != T->nil) {
x->right->parent = y;
}
x->parent = y->parent;
if (y->parent == T->nil) {
T->root = x;
} else if (y == y->parent->right) {
y->parent->right = x;
} else {
y->parent->left = x;
}
x->right = y;
y->parent = x;
}
插入
插入分为两步
1 叶子节点的插入,新节点初始为红色
2 维持黑高的旋转
叶子节点插入
// 先插入到末端,再旋转
void rbtree_insert(rbtree *T, rbtree_node *z) {
rbtree_node *y = T->nil;
rbtree_node *x = T->root;
while (x != T->nil) {
y = x;
if (z->key < x->key) {
x = x->left;
} else if (z->key > x->key) {
x = x->right;
} else { //Exist
return ;
}
}
z->parent = y;
if (y == T->nil) {
T->root = z;
} else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
z->left = T->nil;
z->right = T->nil;
z->color = RED;//默认红色,红色不占高
rbtree_insert_fixup(T, z); //插入不会旋转,插入之后的调整会引起旋转
}
维持树高进行旋转
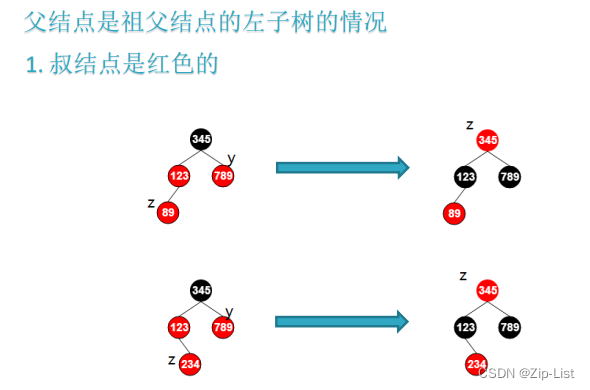
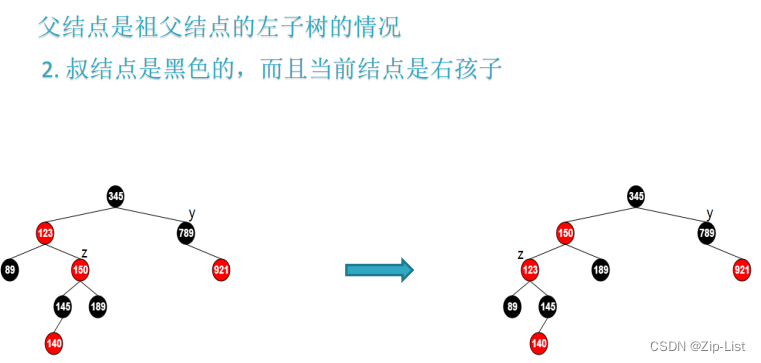
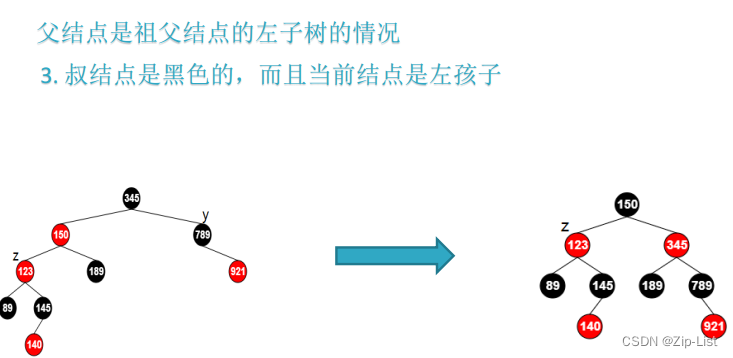
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
// 当前节点肯定是红色
// 父节点是黑色,不用调整
// 父节点红色前提下,祖父肯定是黑色
// 父节点是祖父节点的左子树
// 叔节点红: 不用考虑当前节点是左右孩子 叔父节点高度相同 通过变色就能保证高度
// 叔节点黑
// 且当前节点是右孩子 左旋
// 且当前节点是左孩子 右旋
while (z->parent->color == RED) { //z ---> RED //当前这个z节点无论怎么调整,永远红色
if (z->parent == z->parent->parent->left) { //父节点是左子树
rbtree_node *y = z->parent->parent->right;//叔节点红 不用旋转只用变色
if (y->color == RED) {
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED //循环检查祖父节点
} else { //叔节点黑
if (z == z->parent->right) {
z = z->parent;
rbtree_left_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_right_rotate(T, z->parent->parent);
}
}else {
rbtree_node *y = z->parent->parent->left;
if (y->color == RED) { //叔节点红 不用旋转只用变色
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED
} else {
if (z == z->parent->left) {
z = z->parent;
rbtree_right_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_left_rotate(T, z->parent->parent);
}
}
}
T->root->color = BLACK;
}
删除
替换节点删除
删除后继节点
rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) { //z覆盖节点 y删除节点(z的后继节点) x轴心节点
rbtree_node *y = T->nil;
rbtree_node *x = T->nil;
if ((z->left == T->nil) || (z->right == T->nil)) {
y = z;
} else {
y = rbtree_successor(T, z);
}
if (y->left != T->nil) {
x = y->left;
} else if (y->right != T->nil) {
x = y->right;
}
x->parent = y->parent;
if (y->parent == T->nil) {
T->root = x;
} else if (y == y->parent->left) {
y->parent->left = x;
} else {
y->parent->right = x;
}//此时y已经和这棵树没关系了
if (y != z) {
z->key = y->key;
z->value = y->value;
}//z被y的值覆盖,相当于删除了z
if (y->color == BLACK) { // 删除的节点是黑色的影响树高,需要调整
rbtree_delete_fixup(T, x);
}
return y;
}
维持树高进行旋转
void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {
while ((x != T->root) && (x->color == BLACK)) {
if (x == x->parent->left) {
rbtree_node *w= x->parent->right;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rbtree_left_rotate(T, x->parent);
w = x->parent->right;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
} else {
if (w->right->color == BLACK) {
w->left->color = BLACK;
w->color = RED;
rbtree_right_rotate(T, w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->right->color = BLACK;
rbtree_left_rotate(T, x->parent);
x = T->root;
}
} else {
rbtree_node *w = x->parent->left;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rbtree_right_rotate(T, x->parent);
w = x->parent->left;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
} else {
if (w->left->color == BLACK) {
w->right->color = BLACK;
w->color = RED;
rbtree_left_rotate(T, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->left->color = BLACK;
rbtree_right_rotate(T, x->parent);
x = T->root;
}
}
}
x->color = BLACK;
}
整体
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define RED 1
#define BLACK 2
typedef int KEY_TYPE;
typedef struct _rbtree_node {
unsigned char color;
struct _rbtree_node *right;
struct _rbtree_node *left;
struct _rbtree_node *parent; //和二叉树的不同点
KEY_TYPE key;
void *value;
} rbtree_node;
typedef struct _rbtree {
rbtree_node *root;
rbtree_node *nil;
} rbtree;
rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {
while (x->left != T->nil) {
x = x->left;
}
return x;
}
rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) {
while (x->right != T->nil) {
x = x->right;
}
return x;
}
rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x) {
rbtree_node *y = x->parent; //后继节点1 右子树的最左边
// x
// tmp
// y
if (x->right != T->nil) {
return rbtree_mini(T, x->right);
}
//后继节点2 没有右子树。自己所在左子树的父节点
// y
// tmp
// x
while ((y != T->nil) && (x == y->right)) {
x = y;
y = y->parent;
}
return y;
}
void rbtree_left_rotate(rbtree *T, rbtree_node *x) {
//总共改变6个指针的指向
rbtree_node *y = x->right; // x --> y , y --> x, right --> left, left --> right
x->right = y->left; //1 1
if (y->left != T->nil) { //1 2
y->left->parent = x;
}
y->parent = x->parent; //1 3
if (x->parent == T->nil) { //1 4 //x是root节点
T->root = y;
} else if (x == x->parent->left) { //判断x是父节点的左子树还是右子树
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x; //1 5
x->parent = y; //1 6
}
//右旋 在 左旋的基础上 x/y互换 left/right互换
void rbtree_right_rotate(rbtree *T, rbtree_node *y) {
rbtree_node *x = y->left;
y->left = x->right;
if (x->right != T->nil) {
x->right->parent = y;
}
x->parent = y->parent;
if (y->parent == T->nil) {
T->root = x;
} else if (y == y->parent->right) {
y->parent->right = x;
} else {
y->parent->left = x;
}
x->right = y;
y->parent = x;
}
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
// 当前节点肯定是红色
// 父节点是黑色,不用调整
// 父节点红色前提下,祖父肯定是黑色
// 父节点是祖父节点的左子树
// 叔节点红: 不用考虑当前节点是左右孩子 叔父节点高度相同 通过变色就能保证高度
// 叔节点黑
// 且当前节点是右孩子 左旋
// 且当前节点是左孩子 右旋
while (z->parent->color == RED) { //z ---> RED //当前这个z节点无论怎么调整,永远红色
if (z->parent == z->parent->parent->left) { //父节点是左子树
rbtree_node *y = z->parent->parent->right;//叔节点红 不用旋转只用变色
if (y->color == RED) {
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED //循环检查祖父节点
} else { //叔节点黑
if (z == z->parent->right) {
z = z->parent;
rbtree_left_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_right_rotate(T, z->parent->parent);
}
}else {
rbtree_node *y = z->parent->parent->left;
if (y->color == RED) { //叔节点红 不用旋转只用变色
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED
} else {
if (z == z->parent->left) {
z = z->parent;
rbtree_right_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_left_rotate(T, z->parent->parent);
}
}
}
T->root->color = BLACK;
}
// 先插入到末端,再旋转
void rbtree_insert(rbtree *T, rbtree_node *z) {
rbtree_node *y = T->nil;
rbtree_node *x = T->root;
while (x != T->nil) {
y = x;
if (z->key < x->key) {
x = x->left;
} else if (z->key > x->key) {
x = x->right;
} else { //Exist
return ;
}
}
z->parent = y;
if (y == T->nil) {
T->root = z;
} else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
z->left = T->nil;
z->right = T->nil;
z->color = RED;//默认红色,红色不占高
rbtree_insert_fixup(T, z); //插入不会旋转,插入之后的调整会引起旋转
}
void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {
while ((x != T->root) && (x->color == BLACK)) {
if (x == x->parent->left) {
rbtree_node *w= x->parent->right;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rbtree_left_rotate(T, x->parent);
w = x->parent->right;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
} else {
if (w->right->color == BLACK) {
w->left->color = BLACK;
w->color = RED;
rbtree_right_rotate(T, w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->right->color = BLACK;
rbtree_left_rotate(T, x->parent);
x = T->root;
}
} else {
rbtree_node *w = x->parent->left;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rbtree_right_rotate(T, x->parent);
w = x->parent->left;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
} else {
if (w->left->color == BLACK) {
w->right->color = BLACK;
w->color = RED;
rbtree_left_rotate(T, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->left->color = BLACK;
rbtree_right_rotate(T, x->parent);
x = T->root;
}
}
}
x->color = BLACK;
}
rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) { //z覆盖节点 y删除节点(z的后继节点) x轴心节点
rbtree_node *y = T->nil;
rbtree_node *x = T->nil;
if ((z->left == T->nil) || (z->right == T->nil)) {
y = z;
} else {
y = rbtree_successor(T, z);
}
if (y->left != T->nil) {
x = y->left;
} else if (y->right != T->nil) {
x = y->right;
}
x->parent = y->parent;
if (y->parent == T->nil) {
T->root = x;
} else if (y == y->parent->left) {
y->parent->left = x;
} else {
y->parent->right = x;
}
if (y != z) {
z->key = y->key;
z->value = y->value;
}
if (y->color == BLACK) { // 删除的节点是黑色的影响树高,需要调整
rbtree_delete_fixup(T, x);
}
return y;
}
rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) {
rbtree_node *node = T->root;
while (node != T->nil) {
if (key < node->key) {
node = node->left;
} else if (key > node->key) {
node = node->right;
} else {
return node;
}
}
return T->nil;
}
void rbtree_traversal(rbtree *T, rbtree_node *node) {
if (node != T->nil) {
rbtree_traversal(T, node->left);
printf("key:%d, color:%d\n", node->key, node->color);
rbtree_traversal(T, node->right);
}
}
int main() {
int keyArray[20] = {24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15};
rbtree *T = (rbtree *)malloc(sizeof(rbtree));
if (T == NULL) {
printf("malloc failed\n");
return -1;
}
T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));
T->nil->color = BLACK;
T->root = T->nil;
rbtree_node *node = T->nil;
int i = 0;
for (i = 0;i < 20;i ++) {
node = (rbtree_node*)malloc(sizeof(rbtree_node));
node->key = keyArray[i];
node->value = NULL;
rbtree_insert(T, node);
}
rbtree_traversal(T, T->root);
printf("----------------------------------------\n");
for (i = 0;i < 20;i ++) {
rbtree_node *node = rbtree_search(T, keyArray[i]);
rbtree_node *cur = rbtree_delete(T, node);
free(cur);
rbtree_traversal(T, T->root);
printf("----------------------------------------\n");
}
}
b树
一颗M阶B树T,满足以下条件
\1. 每个结点至多拥有M课子树
\2. 根结点至少拥有两颗子树
\3. 除了根结点以外,其余每个分支结点至少拥有M/2课子树
\4. 所有的叶结点都在同一层上
\5. 有k课子树的分支结点则存在k-1个关键字,关键字按照递增顺序进行排序
\6. 关键字数量满足ceil(M/2)-1 <= n <= M-1
节点结构
多叉树,所以一个节点存储着
值的数组
子树的数组
#define DEGREE 3 //M = 6
typedef int KEY_VALUE;
// b树 多叉树,降低层高,减少寻址次数,有利于磁盘读写
typedef struct _btree_node {
KEY_VALUE *keys; //KEY的数组
struct _btree_node **childrens; //子树指针数组
int num; //KEY的实际数量
int leaf; //是否是叶子节点
} btree_node;
typedef struct _btree {
btree_node *root;
int t;
} btree;
分裂
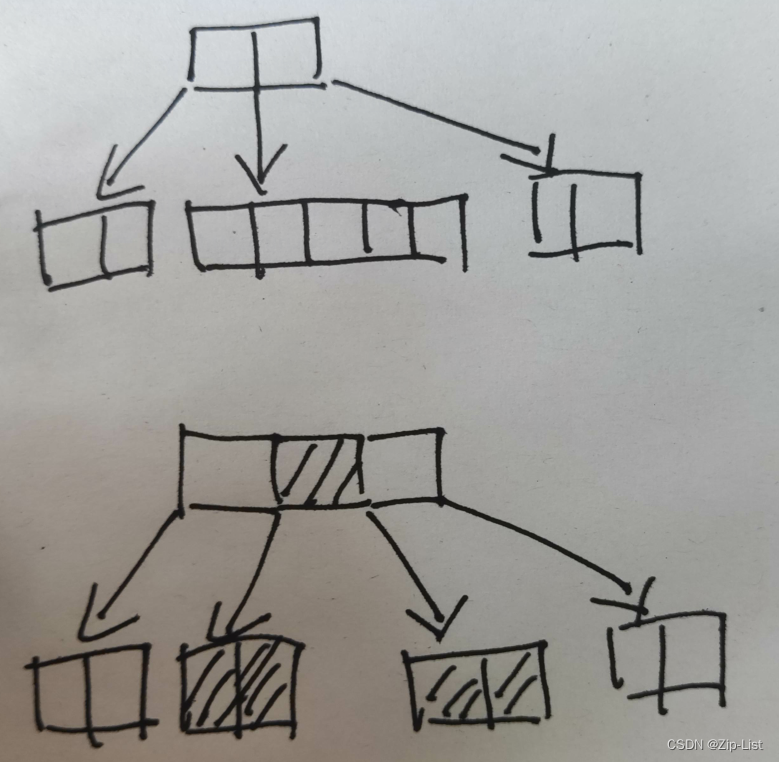
void btree_split_child(btree *T, btree_node *x, int i) { //针对T树的 x节点的 第i个子节点做分裂
int t = T->t;
btree_node *y = x->childrens[i];
btree_node *z = btree_create_node(t, y->leaf);
z->num = t - 1;
int j = 0;
for (j = 0;j < t-1;j ++) {
z->keys[j] = y->keys[j+t];
}
if (y->leaf == 0) {
for (j = 0;j < t;j ++) {
z->childrens[j] = y->childrens[j+t];
}
}
y->num = t - 1;
for (j = x->num;j >= i+1;j --) {
x->childrens[j+1] = x->childrens[j];
}
x->childrens[i+1] = z;
for (j = x->num-1;j >= i;j --) {
x->keys[j+1] = x->keys[j];
}
x->keys[i] = y->keys[t-1];
x->num += 1;
}
插入
插入结点是先分裂再插入
根节点分裂和叶节点分裂有所不同
!插入结点永远都是在叶子节点处插
先分裂,在插入
//插入结点是先分裂再插入
//根节点分裂和叶节点分裂有所不同
//!插入结点永远都是在叶子节点处插
void btree_insert(btree *T, KEY_VALUE key) {
//int t = T->t;
btree_node *r = T->root;
if (r->num == 2 * T->t - 1) { //key数量足够多要分裂了 对根节点做特殊处理 创建一个新节点当做根,以便符合btree_split_child的形式
btree_node *node = btree_create_node(T->t, 0);
T->root = node;
node->childrens[0] = r;
btree_split_child(T, node, 0);
int i = 0;
if (node->keys[0] < key) i++;
btree_insert_nonfull(T, node->childrens[i], key);
} else {
btree_insert_nonfull(T, r, key);
}
}
往下查找,如果节点满了分裂,有了新的未满的节点,在继续递归插入
直到到达叶子节点为止插入
void btree_insert_nonfull(btree *T, btree_node *x, KEY_VALUE k) { //x只是一个未满的节点
int i = x->num - 1;
if (x->leaf == 1) { //递归到叶子节点为止,进行插入
while (i >= 0 && x->keys[i] > k) {
x->keys[i+1] = x->keys[i];
i --;
}
x->keys[i+1] = k;
x->num += 1;
} else {
while (i >= 0 && x->keys[i] > k) i --;
if (x->childrens[i+1]->num == (2*(T->t))-1) { //在往下走的过程中如果节点满了,分裂,有了新的未满的节点,在继续插入
btree_split_child(T, x, i+1);
if (k > x->keys[i+1]) i++;
}
btree_insert_nonfull(T, x->childrens[i+1], k);
}
}
合并
无人可借
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WK0YrmF5-1656218143777)(.assets/image-20220626122704524.png)]](https://img-blog.csdnimg.cn/294dd11fd8cd4deb8ad31ea184c77a66.png)
//{child[idx], key[idx], child[idx+1]}
void btree_merge(btree *T, btree_node *node, int idx) {
btree_node *left = node->childrens[idx];
btree_node *right = node->childrens[idx+1];
int i = 0;
/data merge
left->keys[T->t-1] = node->keys[idx];
for (i = 0;i < T->t-1;i ++) {
left->keys[T->t+i] = right->keys[i];
}
if (!left->leaf) {
for (i = 0;i < T->t;i ++) {
left->childrens[T->t+i] = right->childrens[i];
}
}
left->num += T->t;
//destroy right
btree_destroy_node(right);
//node
for (i = idx+1;i < node->num;i ++) {
node->keys[i-1] = node->keys[i];
node->childrens[i] = node->childrens[i+1];
}
node->childrens[i+1] = NULL;
node->num -= 1;
if (node->num == 0) {
T->root = left;
btree_destroy_node(node);
}
}
删除
// 1 idx子树 ceil(m/2)-1
// A 借位
// idx-1借 > ceil(m-2)-1
// idx+1借 > ceil(m-2)-1
// B 合并
// [ childs[idx].keys + key[idx] + childs[idx+1].keys ]
// 2 idx子树 > ceil(m-2)-1
// 递归找子树
// 删除的值也会在叶子节点,高层向底层借位,下沉
void btree_delete_key(btree *T, btree_node *node, KEY_VALUE key) {
if (node == NULL) return ;
int idx = 0, i;
while (idx < node->num && key > node->keys[idx]) {
idx ++;
}
if (idx < node->num && key == node->keys[idx]) {
if (node->leaf) {
for (i = idx;i < node->num-1;i ++) {
node->keys[i] = node->keys[i+1];
}
node->keys[node->num - 1] = 0;
node->num--;
if (node->num == 0) { //root
free(node);
T->root = NULL;
}
return ;
} else if (node->childrens[idx]->num >= T->t) { //借
btree_node *left = node->childrens[idx];
node->keys[idx] = left->keys[left->num - 1];
btree_delete_key(T, left, left->keys[left->num - 1]);
} else if (node->childrens[idx+1]->num >= T->t) {//借
btree_node *right = node->childrens[idx+1];
node->keys[idx] = right->keys[0];
btree_delete_key(T, right, right->keys[0]);
} else {//合并
btree_merge(T, node, idx);
btree_delete_key(T, node->childrens[idx], key);
}
} else {
btree_node *child = node->childrens[idx];
if (child == NULL) {
printf("Cannot del key = %d\n", key);
return ;
}
if (child->num == T->t - 1) {
btree_node *left = NULL;
btree_node *right = NULL;
if (idx - 1 >= 0)
left = node->childrens[idx-1];
if (idx + 1 <= node->num)
right = node->childrens[idx+1];
if ((left && left->num >= T->t) ||
(right && right->num >= T->t)) {
int richR = 0;
if (right) richR = 1;
if (left && right) richR = (right->num > left->num) ? 1 : 0;
if (right && right->num >= T->t && richR) { //borrow from next
child->keys[child->num] = node->keys[idx];
child->childrens[child->num+1] = right->childrens[0];
child->num ++;
node->keys[idx] = right->keys[0];
for (i = 0;i < right->num - 1;i ++) {
right->keys[i] = right->keys[i+1];
right->childrens[i] = right->childrens[i+1];
}
right->keys[right->num-1] = 0;
right->childrens[right->num-1] = right->childrens[right->num];
right->childrens[right->num] = NULL;
right->num --;
} else { //borrow from prev
for (i = child->num;i > 0;i --) {
child->keys[i] = child->keys[i-1];
child->childrens[i+1] = child->childrens[i];
}
child->childrens[1] = child->childrens[0];
child->childrens[0] = left->childrens[left->num];
child->keys[0] = node->keys[idx-1];
child->num ++;
node->keys[idx-1] = left->keys[left->num-1];
left->keys[left->num-1] = 0;
left->childrens[left->num] = NULL;
left->num --;
}
} else if ((!left || (left->num == T->t - 1))
&& (!right || (right->num == T->t - 1))) {
if (left && left->num == T->t - 1) {
btree_merge(T, node, idx-1);
child = left;
} else if (right && right->num == T->t - 1) {
btree_merge(T, node, idx);
}
}
}
btree_delete_key(T, child, key);
}
}
整体
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#define DEGREE 3 //M = 6
typedef int KEY_VALUE;
// b树 多叉树,降低层高,减少寻址次数,有利于磁盘读写
typedef struct _btree_node {
KEY_VALUE *keys; //KEY的数组
struct _btree_node **childrens; //子树指针数组
int num; //KEY的实际数量
int leaf; //是否是叶子节点
} btree_node;
typedef struct _btree {
btree_node *root;
int t;
} btree;
btree_node *btree_create_node(int t, int leaf) {
btree_node *node = (btree_node*)calloc(1, sizeof(btree_node));
if (node == NULL) assert(0);
node->leaf = leaf;
node->keys = (KEY_VALUE*)calloc(1, (2*t-1)*sizeof(KEY_VALUE));
node->childrens = (btree_node**)calloc(1, (2*t) * sizeof(btree_node));
node->num = 0;
return node;
}
void btree_destroy_node(btree_node *node) {
assert(node);
free(node->childrens);
free(node->keys);
free(node);
}
void btree_create(btree *T, int t) {
T->t = t;
btree_node *x = btree_create_node(t, 1);
T->root = x;
}
void btree_split_child(btree *T, btree_node *x, int i) { //针对T树的 x节点的 第i个子节点做分裂
int t = T->t;
btree_node *y = x->childrens[i];
btree_node *z = btree_create_node(t, y->leaf);
z->num = t - 1;
int j = 0;
for (j = 0;j < t-1;j ++) {
z->keys[j] = y->keys[j+t];
}
if (y->leaf == 0) {
for (j = 0;j < t;j ++) {
z->childrens[j] = y->childrens[j+t];
}
}
y->num = t - 1;
for (j = x->num;j >= i+1;j --) {
x->childrens[j+1] = x->childrens[j];
}
x->childrens[i+1] = z;
for (j = x->num-1;j >= i;j --) {
x->keys[j+1] = x->keys[j];
}
x->keys[i] = y->keys[t-1];
x->num += 1;
}
void btree_insert_nonfull(btree *T, btree_node *x, KEY_VALUE k) { //x只是一个未满的节点
int i = x->num - 1;
if (x->leaf == 1) { //递归到叶子节点为止,进行插入
while (i >= 0 && x->keys[i] > k) {
x->keys[i+1] = x->keys[i];
i --;
}
x->keys[i+1] = k;
x->num += 1;
} else {
while (i >= 0 && x->keys[i] > k) i --;
if (x->childrens[i+1]->num == (2*(T->t))-1) { //在往下走的过程中如果节点满了,分裂,有了新的未满的节点,在继续插入
btree_split_child(T, x, i+1);
if (k > x->keys[i+1]) i++;
}
btree_insert_nonfull(T, x->childrens[i+1], k);
}
}
//插入结点是先分裂再插入
//根节点分裂和叶节点分裂有所不同
//!插入结点永远都是在叶子节点处插
void btree_insert(btree *T, KEY_VALUE key) {
//int t = T->t;
btree_node *r = T->root;
if (r->num == 2 * T->t - 1) { //key数量足够多要分裂了 对根节点做特殊处理 创建一个新节点当做根,以便符合btree_split_child的形式
btree_node *node = btree_create_node(T->t, 0);
T->root = node;
node->childrens[0] = r;
btree_split_child(T, node, 0);
int i = 0;
if (node->keys[0] < key) i++;
btree_insert_nonfull(T, node->childrens[i], key);
} else {
btree_insert_nonfull(T, r, key);
}
}
void btree_traverse(btree_node *x) {
int i = 0;
for (i = 0;i < x->num;i ++) {
if (x->leaf == 0)
btree_traverse(x->childrens[i]);
printf("%C ", x->keys[i]);
}
if (x->leaf == 0) btree_traverse(x->childrens[i]);
}
void btree_print(btree *T, btree_node *node, int layer)
{
btree_node* p = node;
int i;
if(p){
printf("\nlayer = %d keynum = %d is_leaf = %d\n", layer, p->num, p->leaf);
for(i = 0; i < node->num; i++)
printf("%c ", p->keys[i]);
printf("\n");
#if 0
printf("%p\n", p);
for(i = 0; i <= 2 * T->t; i++)
printf("%p ", p->childrens[i]);
printf("\n");
#endif
layer++;
for(i = 0; i <= p->num; i++)
if(p->childrens[i])
btree_print(T, p->childrens[i], layer);
}
else printf("the tree is empty\n");
}
int btree_bin_search(btree_node *node, int low, int high, KEY_VALUE key) {
int mid;
if (low > high || low < 0 || high < 0) {
return -1;
}
while (low <= high) {
mid = (low + high) / 2;
if (key > node->keys[mid]) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return low;
}
//{child[idx], key[idx], child[idx+1]}
void btree_merge(btree *T, btree_node *node, int idx) {
btree_node *left = node->childrens[idx];
btree_node *right = node->childrens[idx+1];
int i = 0;
/data merge
left->keys[T->t-1] = node->keys[idx];
for (i = 0;i < T->t-1;i ++) {
left->keys[T->t+i] = right->keys[i];
}
if (!left->leaf) {
for (i = 0;i < T->t;i ++) {
left->childrens[T->t+i] = right->childrens[i];
}
}
left->num += T->t;
//destroy right
btree_destroy_node(right);
//node
for (i = idx+1;i < node->num;i ++) {
node->keys[i-1] = node->keys[i];
node->childrens[i] = node->childrens[i+1];
}
node->childrens[i+1] = NULL;
node->num -= 1;
if (node->num == 0) {
T->root = left;
btree_destroy_node(node);
}
}
// 1 idx子树 ceil(m/2)-1
// A 借位
// idx-1借 > ceil(m-2)-1
// idx+1借 > ceil(m-2)-1
// B 合并
// [ childs[idx].keys + key[idx] + childs[idx+1].keys ]
// 2 idx子树 > ceil(m-2)-1
// 递归找子树
// 删除的值也会在叶子节点,高层向底层借位,下沉
void btree_delete_key(btree *T, btree_node *node, KEY_VALUE key) {
if (node == NULL) return ;
int idx = 0, i;
while (idx < node->num && key > node->keys[idx]) {
idx ++;
}
if (idx < node->num && key == node->keys[idx]) {
if (node->leaf) {
for (i = idx;i < node->num-1;i ++) {
node->keys[i] = node->keys[i+1];
}
node->keys[node->num - 1] = 0;
node->num--;
if (node->num == 0) { //root
free(node);
T->root = NULL;
}
return ;
} else if (node->childrens[idx]->num >= T->t) { //借
btree_node *left = node->childrens[idx];
node->keys[idx] = left->keys[left->num - 1];
btree_delete_key(T, left, left->keys[left->num - 1]);
} else if (node->childrens[idx+1]->num >= T->t) {//借
btree_node *right = node->childrens[idx+1];
node->keys[idx] = right->keys[0];
btree_delete_key(T, right, right->keys[0]);
} else {//合并
btree_merge(T, node, idx);
btree_delete_key(T, node->childrens[idx], key);
}
} else {
btree_node *child = node->childrens[idx];
if (child == NULL) {
printf("Cannot del key = %d\n", key);
return ;
}
if (child->num == T->t - 1) {
btree_node *left = NULL;
btree_node *right = NULL;
if (idx - 1 >= 0)
left = node->childrens[idx-1];
if (idx + 1 <= node->num)
right = node->childrens[idx+1];
if ((left && left->num >= T->t) ||
(right && right->num >= T->t)) {
int richR = 0;
if (right) richR = 1;
if (left && right) richR = (right->num > left->num) ? 1 : 0;
if (right && right->num >= T->t && richR) { //borrow from next
child->keys[child->num] = node->keys[idx];
child->childrens[child->num+1] = right->childrens[0];
child->num ++;
node->keys[idx] = right->keys[0];
for (i = 0;i < right->num - 1;i ++) {
right->keys[i] = right->keys[i+1];
right->childrens[i] = right->childrens[i+1];
}
right->keys[right->num-1] = 0;
right->childrens[right->num-1] = right->childrens[right->num];
right->childrens[right->num] = NULL;
right->num --;
} else { //borrow from prev
for (i = child->num;i > 0;i --) {
child->keys[i] = child->keys[i-1];
child->childrens[i+1] = child->childrens[i];
}
child->childrens[1] = child->childrens[0];
child->childrens[0] = left->childrens[left->num];
child->keys[0] = node->keys[idx-1];
child->num ++;
node->keys[idx-1] = left->keys[left->num-1];
left->keys[left->num-1] = 0;
left->childrens[left->num] = NULL;
left->num --;
}
} else if ((!left || (left->num == T->t - 1))
&& (!right || (right->num == T->t - 1))) {
if (left && left->num == T->t - 1) {
btree_merge(T, node, idx-1);
child = left;
} else if (right && right->num == T->t - 1) {
btree_merge(T, node, idx);
}
}
}
btree_delete_key(T, child, key);
}
}
int btree_delete(btree *T, KEY_VALUE key) {
if (!T->root) return -1;
btree_delete_key(T, T->root, key);
return 0;
}
int main() {
btree T = {0};
btree_create(&T, 3);
srand(48);
int i = 0;
char key[26] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
for (i = 0;i < 26;i ++) {
//key[i] = rand() % 1000;
printf("%c ", key[i]);
btree_insert(&T, key[i]);
}
btree_print(&T, T.root, 0);
for (i = 0;i < 26;i ++) {
printf("\n---------------------------------\n");
btree_delete(&T, key[25-i]);
//btree_traverse(T.root);
btree_print(&T, T.root, 0);
}
}