[数据结构与算法]堆排序详解

什么是堆？

堆是一种完全二叉树「即每个节点的所在下标与满二叉树节点的下标一致」

根据堆的性质，可以将堆分成大根堆和小根堆

• 大根堆：每个节点的值大于等于它的左右孩子的值
• 小根堆：每个节点的值小于等于它的左右孩子的值

上图就是一个大根堆，我们可以将其映射到数组 array 中

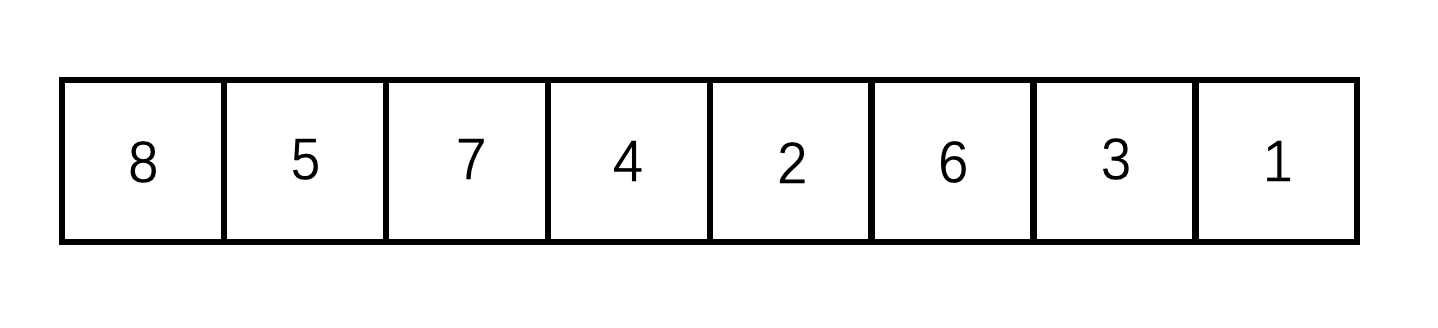
根据大根堆的性质，我们很容易得到以下结论：

array[i] >= array[2 * i + 1] && array[i] >= array[2 * i + 2]

堆排序的基本思想

堆排序大体上可以分为三步：

1. 将待排序的数组构建成一个大根堆，这样堆顶的元素就是最大的元素。
2. 将堆顶元素和最后一个元素交换，然后将除去最后一个元素的剩下节点重新构造为一个大根堆
3. 重复步骤 2 ，直至排序完成。「第一次可以得到最大的元素，第二次可以得到第二大的元素，依此类推」

类比：这个过程就像是，在一群人中找到一个最高的，让他和坐最后一排的人交换位置；然后在剩下的人中找到身高第二高的，让他和坐在倒数第二排的人交换位置；依此类推。

堆排序的详细实现

假设待排序数组 array =[5,8,2,4,3,6,7,1]

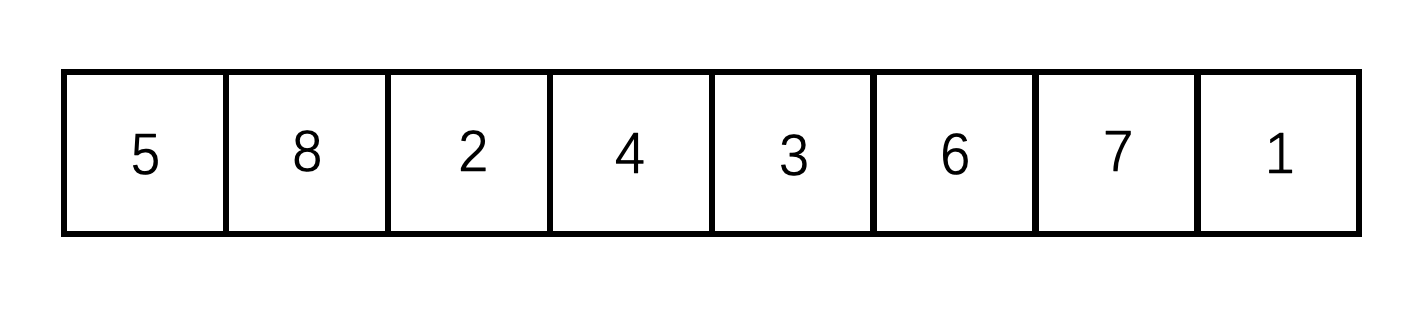
1 将待排序数组构建成一个大根堆

首先，将待排序数组变成一个完全二叉树

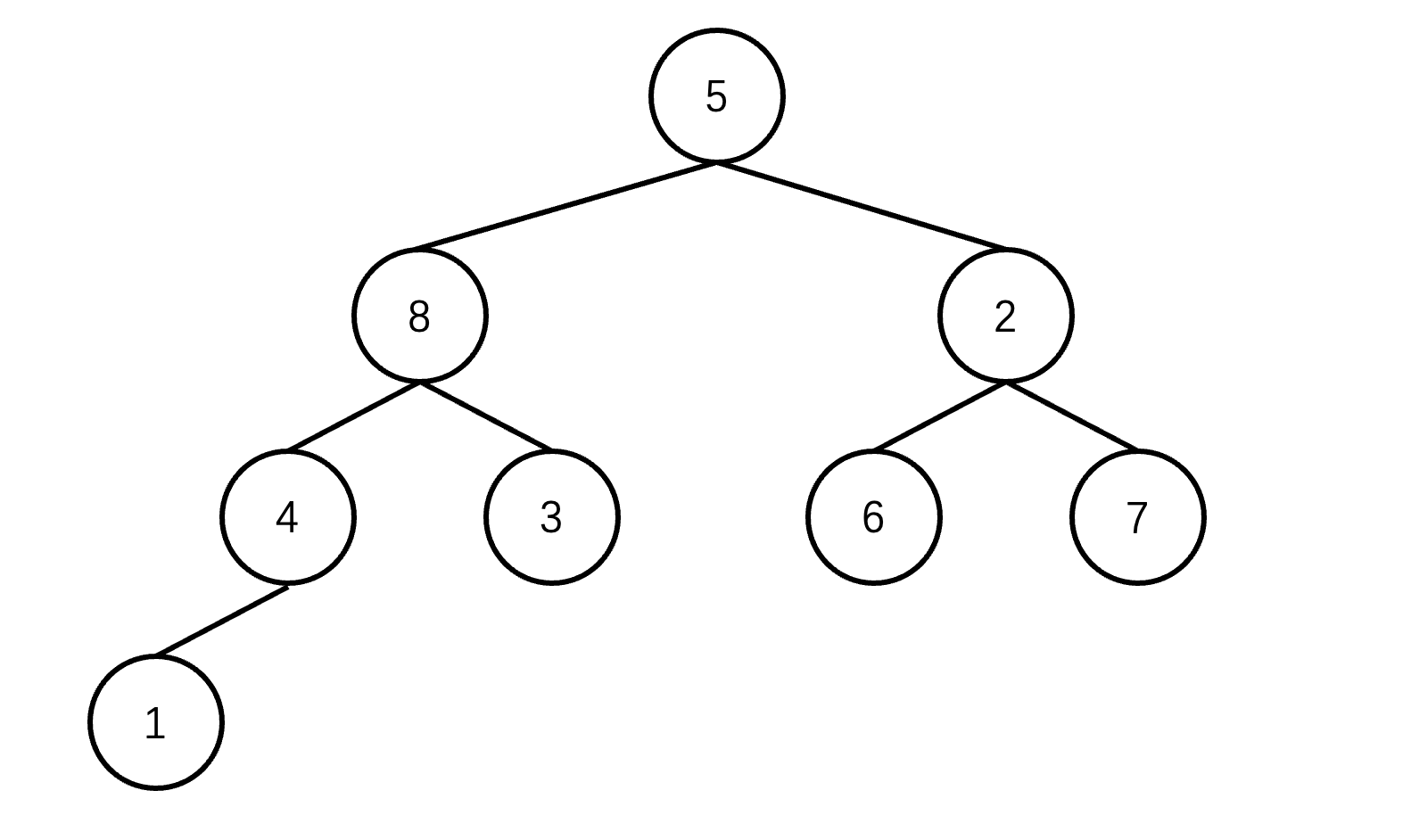
接下来，我们需要保证：每个节点的值比它的左右孩子的值要大。这里你可能会想，我们可以从最上层开始，比较父节点和子节点的大小关系，将较大的元素放在父节点上。这种方法看似是对的，但是我们从上往下遍历的过程中，上层的子节点可能被更大的值替换，导致部分子节点比父节点要大「即无法保证堆顶的值是最大的」。如下图所示

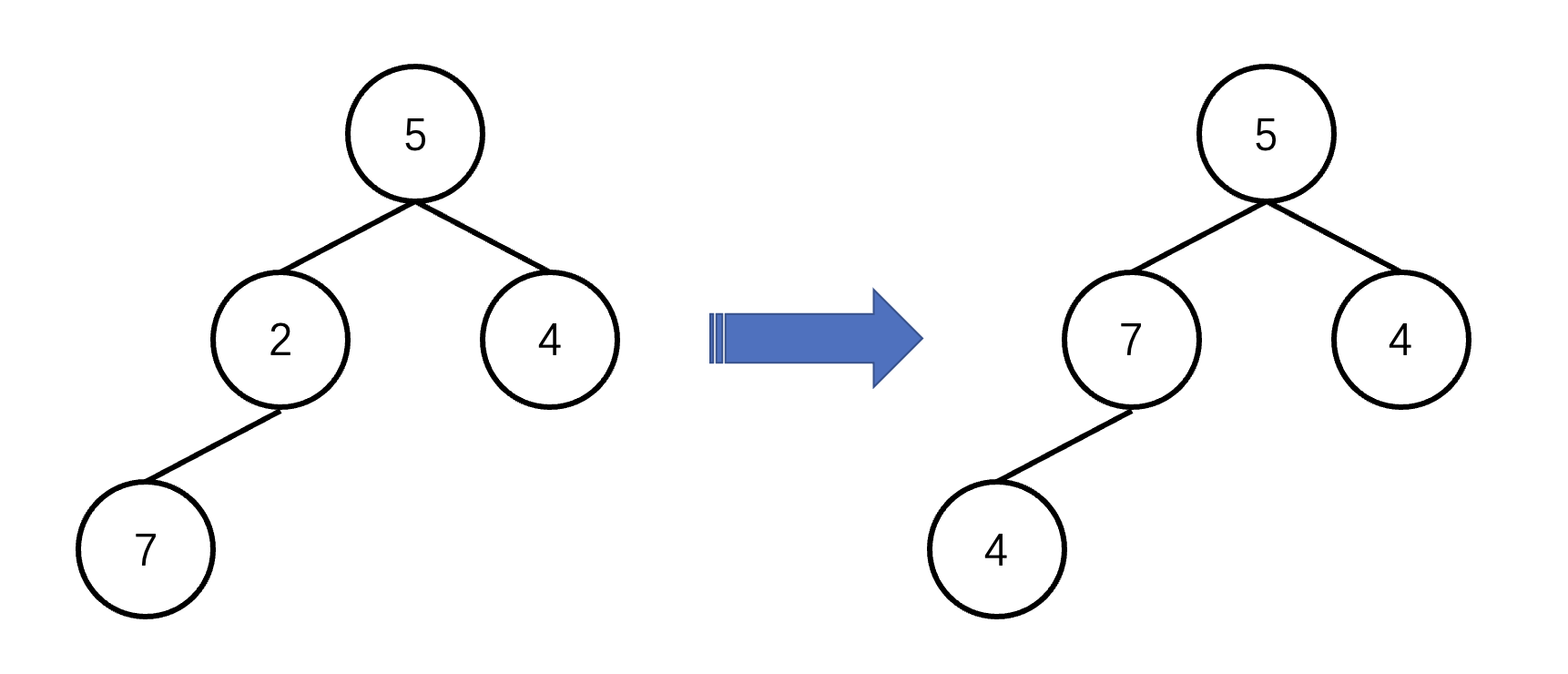
因此，我们必须从下到上进行比较。为此，我们需要找到最后一个父节点，然后倒叙整理父子节点的大小关系。那么该怎么找到最后一个父节点呢？因为，在大根堆中array[i] >= array[2 * i + 1] && array[i] >= array[2 * i + 2]，所以当叶子节点坐标为 length - 1 时**「下标最大的叶子节点」**，其父节点的坐标为 (length / 2) - 1。「根据 i * 2 + 1 = length - 1 和 i * 2 + 2 = length - 1 」

找到最后一个父节点后，比较它和左右节点的值，如果左右节点的值比它大，将左右节点的较大值与它交换；否则不进行任何操作，对于 array ，会交换 7 和 2 的位置

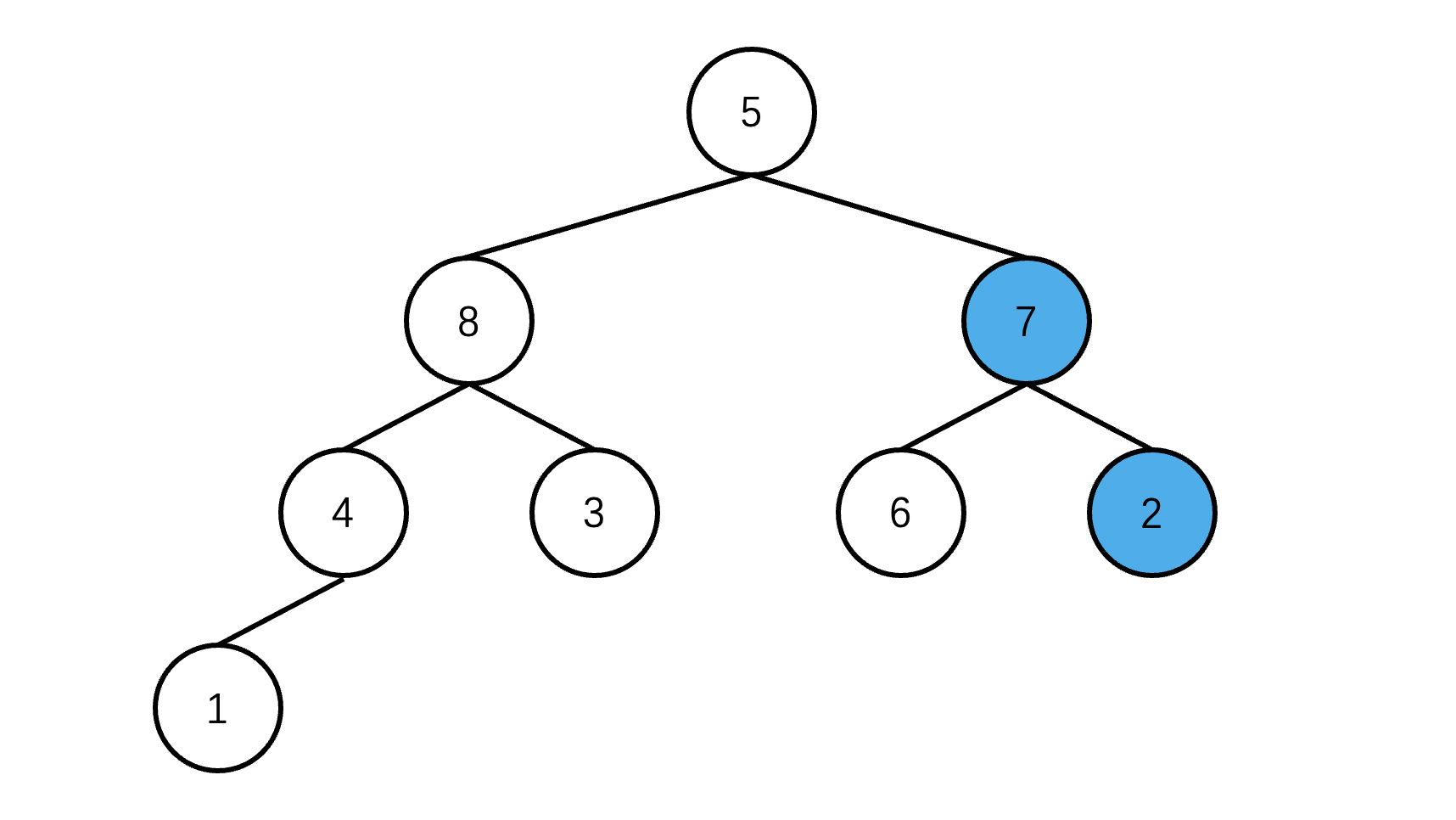
然后交换 8 和 5 的位置

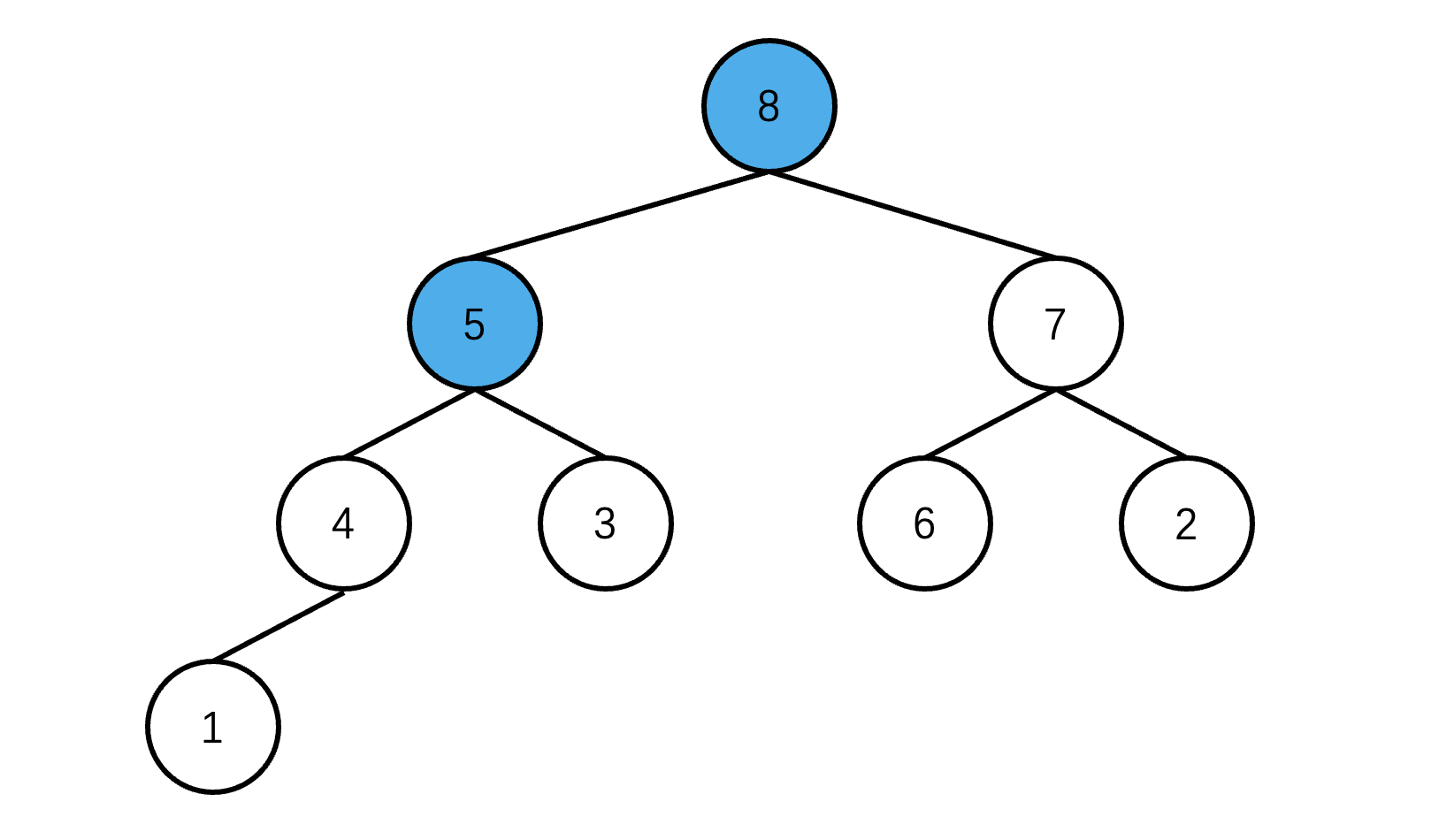
注意，如果交换节点后，下一层的子节点比父节点要大，还要继续进行交换。

将堆顶元素和最后一个元素交换，然后将除去最后一个元素的剩下节点重新构造为一个大根堆

将堆顶元素和最后一个元素进行交换

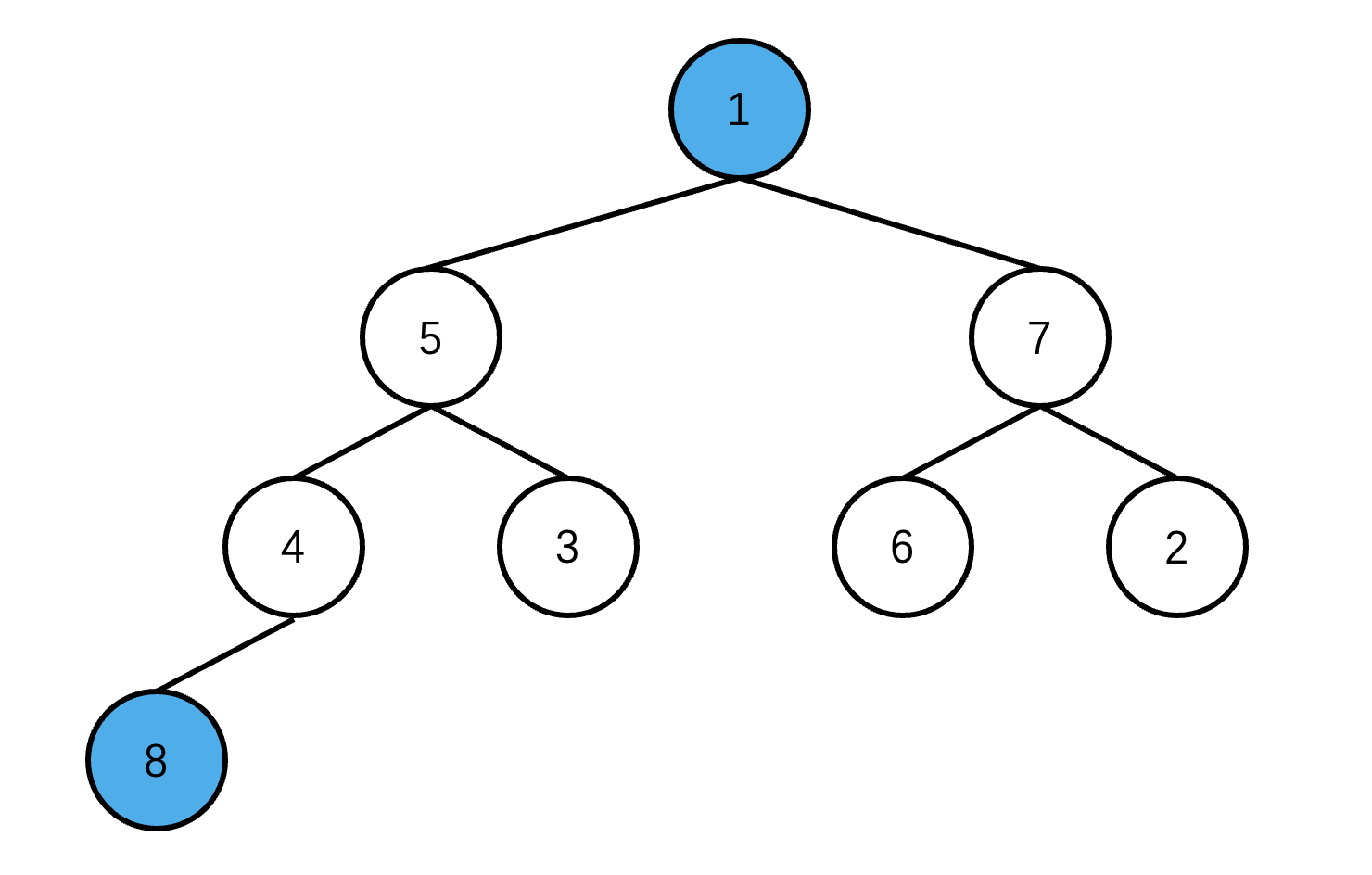
3. 重复步骤 2 ，直至排序完成。

我们用一个动态图感受一下整个过程

代码实现

Kotlin

class Solution {
    fun heapSort(array: IntArray) {
        if (array.isEmpty()) return
        var length = array.size
        buildMaxHeap(array, length)
        for (i in length - 1 downTo 0) { // 这里可以写成 downTo 1 因为到 1 时已经交换完毕
            swap(array, 0, i) // 交换根顶和当前最后的元素
            length--
            heapify(array,0,length) // 因为交换，可能不满足大根堆的条件，对堆顶元素进行调整
        }
    }

    private fun buildMaxHeap(array: IntArray, length: Int) {
        val fatherIndex = (length / 2) + 1 // 找到最后一个父节点所在下标
        for (i in fatherIndex downTo 0) {
            heapify(array, i, length)
        }
    }

    private fun swap(array: IntArray, i: Int, j: Int) {
        val temp = array[i]
        array[i] = array[j]
        array[j] = temp
    }

    private fun heapify(array: IntArray, i: Int, length: Int) {
        val left = 2 * i + 1 // 左节点
        val right = 2 * i + 2 // 右节点
        var largeIndex = i // 父节点与左右节点中的最大值对应的下标
        if (left < length && array[left] > array[largeIndex]) largeIndex = left
        if (right < length && array[right] > array[largeIndex]) largeIndex = right
        if (largeIndex != i) {
            swap(array, largeIndex, i) // 交换后，可能导致下层不是大根堆
            heapify(array, largeIndex, length)
        }
    }
}