[数据结构与算法]SizeBalanceTree

SBT树的概念及其相关性质

众所周知二叉搜索树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(logN)。缺点是若待插入的序列是有序的，那么它会退化成单链表，这样查询时间将会退化为O(N)。

AVL树和红黑树对二叉搜索树进行了升级，增加平衡和旋转操作。但是红黑树实现起来比较复杂，AVL过于平衡导致旋转的开销过大。

SBT树是一个相对来讲容易实现，并且平衡性又不错的树。

SBT树相关性质：
任何一个叔叔节点为根的子树节点的个数不能少于侄子节点的个数，比如：

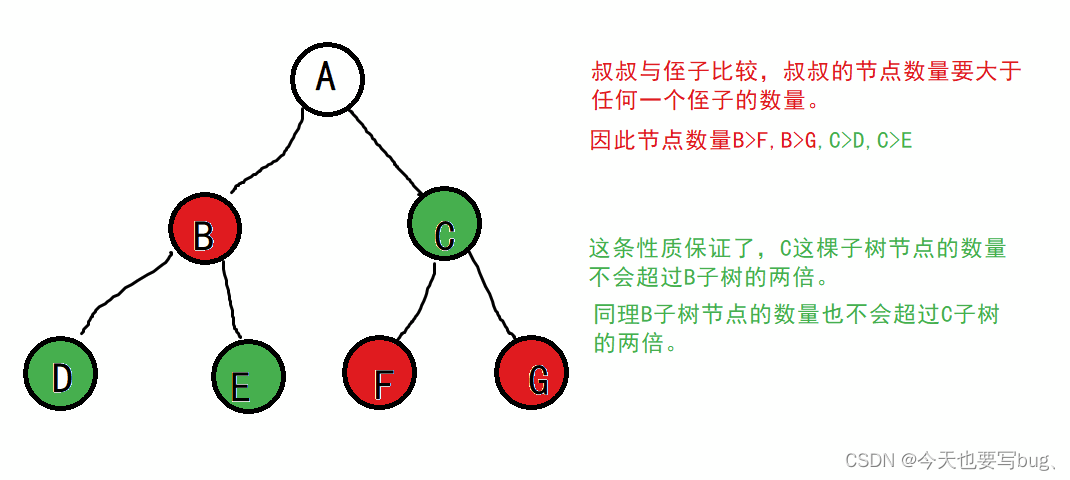
节点的定义

struct SBTNode
{
	SBTNode(const pair<K, V>kv = pair<K, V>())
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_size(1)
	{}
	pair<K, V>_kv;
	SBTNode<K, V>* _left;
	SBTNode<K, V>* _right;
	int _size;//节点的个数
};

旋转操作

1. LL型违规
   LL型违规顾名思义就是根节点左孩子的左孩子的size比根节点右孩子大。

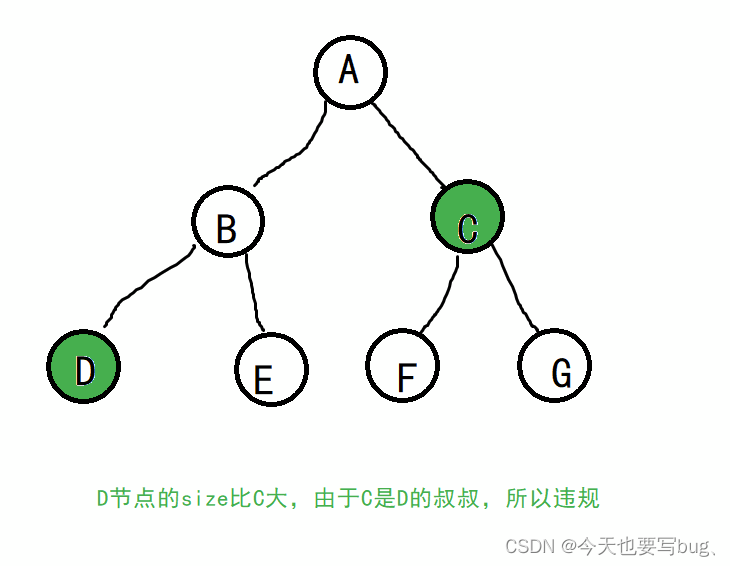
此时我们对根节点进行右旋，让D节点来做叔叔节点，C节点作为D的侄子节点。

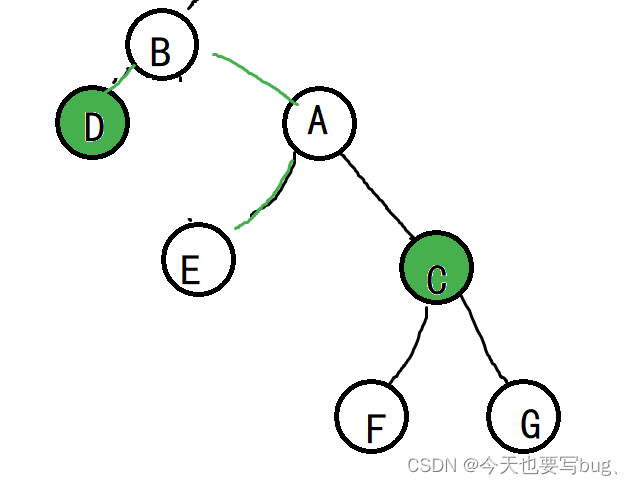
但是进行右旋之后，我们会发现B和A的孩子发生了变化，此时需要递归检查它们是否符合BST的性质。

2. RR型违规
   根节点右孩子的右孩子的size比根节点的左孩子大。

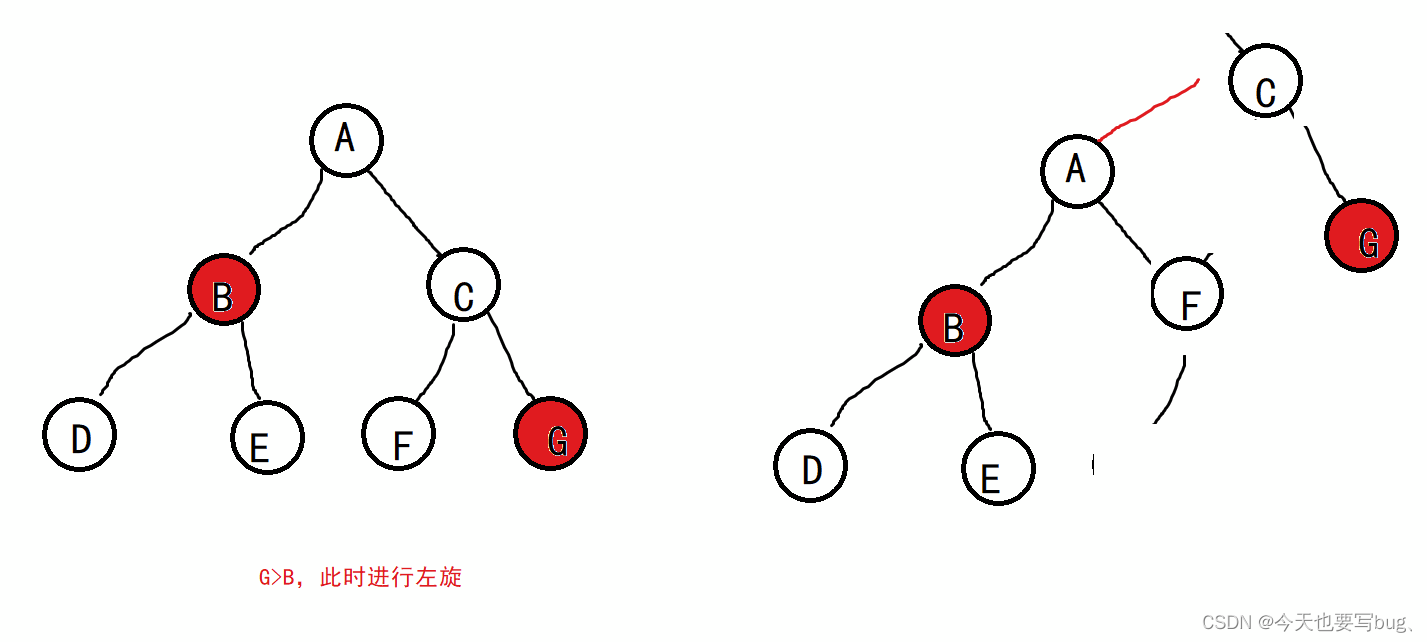
同样的我们也需要对C和A进行递归检查操作。

3. LR型违规
   LR型是指根节点左孩子的右孩子节点的个数大于根节点右孩子的个数。
   

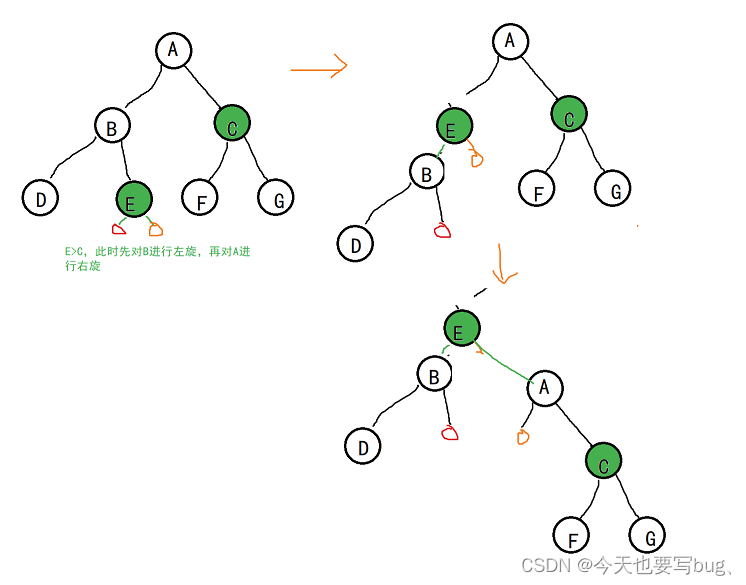
经过旋转之后ABE这三个节点的左右孩子发生了变化，因此需要对其进行递归检查。

4. RL型违规
   RL型是指根节点右孩子的左孩子节点的个数大于根节点左孩子的个数。
   
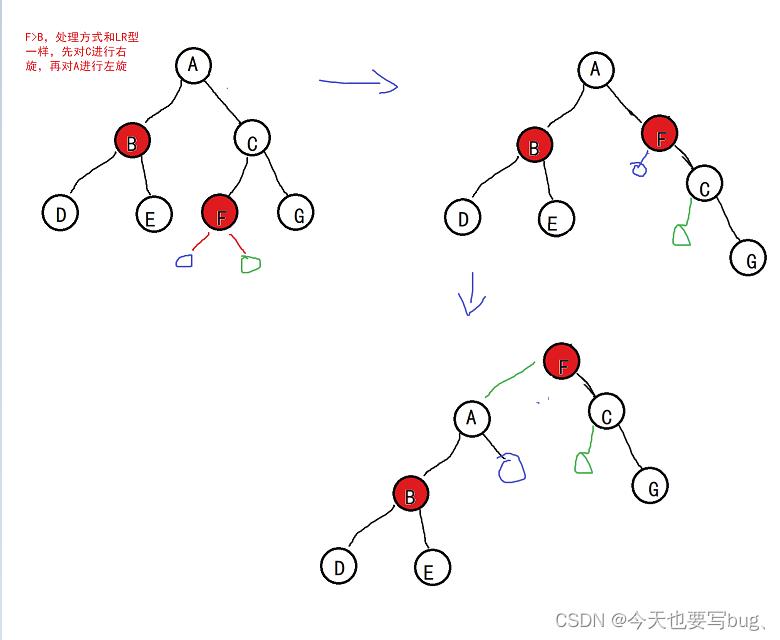
   经过旋转之后ACF这三个节点的左右孩子发生了变化，因此需要对其进行递归检查。

代码操作：

	//右旋
	Node* rightRotate(Node* cur) 
	{
		//找到新的根节点
		Node* leftNode = cur->_left;
		cur->_left = leftNode->_right;
		leftNode->_right = cur;
		//根节点的size更新
		leftNode->_size = cur->_size;
		//cur的size更新
		cur->_size = (cur->_left ? cur->_left->_size : 0) + (cur->_right ? cur->_right->_size : 0) + 1;

		return leftNode;
	}
	//左旋
	Node* leftRotate(Node* cur) 
	{
		Node* rightNode = cur->_right;
		cur->_right = rightNode->_left;
		rightNode->_left = cur;
		rightNode->_size = cur->_size;
		cur->_size = (cur->_left ? cur->_left->_size : 0) + (cur->_right ? cur->_right->_size : 0) + 1;
		return rightNode;
	}
	//调整节点的操作
	Node* maintain(Node* cur)
	{
		if (cur == nullptr)
		{
			return nullptr;
		}
		//将节点的个数拿出来
		//左孩子
		int leftSize = cur->_left != nullptr ? cur->_left->_size : 0;
		//左孩子的左孩子
		int leftLeftSize = cur->_left && cur->_left->_left ? cur->_left->_left->_size : 0;
		//左孩子的右孩子
		int leftRightSize = cur->_left && cur->_left->_right ? cur->_left->_right->_size : 0;
		//右孩子
		int rightSize = cur->_right ? cur->_right->_size : 0;
		//右孩子的左孩子
		int rightLeftSize = cur->_right && cur->_right->_left ? cur->_right->_left->_size : 0;
		//右孩子的右孩子
		int rightRightSize = cur->_right && cur->_right->_right ? cur->_right->_right->_size : 0;
		//LL型违规
		if (leftLeftSize > rightSize)
		{
			//右旋
			cur = rightRotate(cur);
			//递归检查
			cur->_right = maintain(cur->_right);
			cur = maintain(cur);
		}
		//LR型
		else if (leftRightSize > rightSize) 
		{
			//左右双旋
			cur->_left = leftRotate(cur->_left);
			cur = rightRotate(cur);
			//递归检查
			cur->_left = maintain(cur->_left);
			cur->_right = maintain(cur->_right);
			cur = maintain(cur);
		}
		//RR型
		else if (rightRightSize > leftSize) 
		{
			cur = leftRotate(cur);
			cur->_left = maintain(cur->_left);
			cur = maintain(cur);
		}
		//RL型
		else if (rightLeftSize > leftSize) 
		{
			cur->_right = rightRotate(cur->_right);
			cur = leftRotate(cur);
			cur->_left = maintain(cur->_left);
			cur->_right = maintain(cur->_right);
			cur = maintain(cur);
		}
		return cur;//返回调整后的头部
	}

插入和删除操作

插入与删除操作与AVL树相同，不过插入时要对路径上的节点中的size+1，删除时-1，并且在返回前对他们进行调整。

//新增节点的操作，在找寻插入位置时要对路径上节点的size++
	//并且找到后，对整棵树进行调整，因为新增节点会破坏BST的性质
	Node* add(Node*& cur, const pair<K, V>& kv) 
	{
		if (cur == nullptr) 
		{
			return new Node(kv);
		}
		else 
		{
			//由于要递归向下找插入的位置
			//因此对沿途节点的size自增
			cur->_size++;
			if (cur->_kv.first > kv.first) 
			{
				cur->_left = add(cur->_left, kv);//去左边插入
			}
			else 
			{
				cur->_right = add(cur->_right, kv);//去右边插入
			}
		}
		//返回前进行调整
		return maintain(cur);
	}
	//插入节点
	bool insert(const pair<K, V>& kv) 
	{
		//先找一下这个节点，如果存在就直接返回
		Node* lastNode = findLastIndex(kv.first);
		//已经存在
		if (lastNode && lastNode->_kv.first == kv.first) 
		{
			return false;
		}
		_root = add(_root, kv);
		return true;
	}

	//删除节点
	Node* deleteNode(Node*& cur, const K& key)
	{
		//删除路径上节点的size减少
		cur->_size--;
		if (cur->_kv.first > key) 
		{
			cur->_left = deleteNode(cur->_left, key);
		}
		else if (cur->_kv.first < key) 
		{
			cur->_right = deleteNode(cur->_right, key);//左边删并将新的头部返回
		}
		else 
		{
			//左为空并且右为空，直接删
			if (!cur->_left && !cur->_right) 
			{
				delete cur;
				cur = nullptr;
			}
			//左为空但右不为空,拿右节点代替
			else if (!cur->_left && cur->_right) 
			{
				Node* subR = cur->_right;
				delete cur;
				cur = subR;
			}
			//左不为空右为空，拿左节点代替
			else if (cur->_left && !cur->_right) 
			{
				Node* subL = cur->_left;
				delete cur;
				cur = subL;
			}
			//左右都不为空
			else 
			{
				Node* pre = nullptr;
				//找右子树的最左节点，并且路径上的值--
				Node* des = cur->_right;
				des->_size--;
				while (des->_left) 
				{
					pre = des;
					des = des->_left;
					des->_size--;
				}
				//替换法删除
				//将des换到头结点，des的位置用右子树替代
				if (pre) 
				{
					pre->_left = des->_right;
					des->_right = cur->_right;
				}
				des->_left = cur->_left;
				//更新size
				des->_size = des->_left->_size + (des->_right ? des->_right->_size : 0) + 1;

				delete cur;
				cur = des;
			}
		}
		//在返回前进行调整
		cur = maintain(cur);

		return cur;//返回新头部
	}

总代码

#pragma once 
#include<math.h>
#include<iostream>
#include<vector>
using namespace std;
template<class K, class V>
struct SBTNode
{
	SBTNode(const pair<K, V>kv = pair<K, V>())
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _size(1)
	{}
	pair<K, V>_kv;
	SBTNode<K, V>* _left;
	SBTNode<K, V>* _right;
	int _size;//节点的个数
};
template<class K, class V>
class SizeBalancedTreeMap {
	typedef SBTNode<K, V> Node;
public:
	//右旋
	Node* rightRotate(Node* cur) 
	{
		//找到新的根节点
		Node* leftNode = cur->_left;
		cur->_left = leftNode->_right;
		leftNode->_right = cur;
		//根节点的size更新
		leftNode->_size = cur->_size;
		//cur的size更新
		cur->_size = (cur->_left ? cur->_left->_size : 0) + (cur->_right ? cur->_right->_size : 0) + 1;

		return leftNode;
	}
	//左旋
	Node* leftRotate(Node* cur) 
	{
		Node* rightNode = cur->_right;
		cur->_right = rightNode->_left;
		rightNode->_left = cur;
		rightNode->_size = cur->_size;
		cur->_size = (cur->_left ? cur->_left->_size : 0) + (cur->_right ? cur->_right->_size : 0) + 1;
		return rightNode;
	}
	//调整节点的操作
	Node* maintain(Node* cur)
	{
		if (cur == nullptr)
		{
			return nullptr;
		}
		//将节点的个数拿出来
		//左孩子
		int leftSize = cur->_left != nullptr ? cur->_left->_size : 0;
		//左孩子的左孩子
		int leftLeftSize = cur->_left && cur->_left->_left ? cur->_left->_left->_size : 0;
		//左孩子的右孩子
		int leftRightSize = cur->_left && cur->_left->_right ? cur->_left->_right->_size : 0;
		//右孩子
		int rightSize = cur->_right ? cur->_right->_size : 0;
		//右孩子的左孩子
		int rightLeftSize = cur->_right && cur->_right->_left ? cur->_right->_left->_size : 0;
		//右孩子的右孩子
		int rightRightSize = cur->_right && cur->_right->_right ? cur->_right->_right->_size : 0;
		//LL型违规
		if (leftLeftSize > rightSize)
		{
			//右旋
			cur = rightRotate(cur);
			//递归检查
			cur->_right = maintain(cur->_right);
			cur = maintain(cur);
		}
		//LR型
		else if (leftRightSize > rightSize) 
		{
			//左右双旋
			cur->_left = leftRotate(cur->_left);
			cur = rightRotate(cur);
			//递归检查
			cur->_left = maintain(cur->_left);
			cur->_right = maintain(cur->_right);
			cur = maintain(cur);
		}
		//RR型
		else if (rightRightSize > leftSize) 
		{
			cur = leftRotate(cur);
			cur->_left = maintain(cur->_left);
			cur = maintain(cur);
		}
		//RL型
		else if (rightLeftSize > leftSize) 
		{
			cur->_right = rightRotate(cur->_right);
			cur = leftRotate(cur);
			cur->_left = maintain(cur->_left);
			cur->_right = maintain(cur->_right);
			cur = maintain(cur);
		}
		return cur;//返回调整后的头部
	}

	//新增节点的操作，在找寻插入位置时要对路径上节点的size++
	//并且找到后，对整棵树进行调整，因为新增节点会破坏BST的性质
	Node* add(Node*& cur, const pair<K, V>& kv) 
	{
		if (cur == nullptr) 
		{
			return new Node(kv);
		}
		else 
		{
			//由于要递归向下找插入的位置
			//因此对沿途节点的size自增
			cur->_size++;
			if (cur->_kv.first > kv.first) 
			{
				cur->_left = add(cur->_left, kv);//去左边插入
			}
			else 
			{
				cur->_right = add(cur->_right, kv);//去右边插入
			}
		}
		//返回前进行调整
		return maintain(cur);
	}
	//插入节点
	bool insert(const pair<K, V>& kv) 
	{
		//先找一下这个节点，如果存在就直接返回
		Node* lastNode = findLastIndex(kv.first);
		//已经存在
		if (lastNode && lastNode->_kv.first == kv.first) 
		{
			return false;
		}
		_root = add(_root, kv);
		return true;
	}

	//删除节点
	Node* deleteNode(Node*& cur, const K& key)
	{
		//删除路径上节点的size减少
		cur->_size--;
		if (cur->_kv.first > key) 
		{
			cur->_left = deleteNode(cur->_left, key);
		}
		else if (cur->_kv.first < key) 
		{
			cur->_right = deleteNode(cur->_right, key);//左边删并将新的头部返回
		}
		else 
		{
			//左为空并且右为空，直接删
			if (!cur->_left && !cur->_right) 
			{
				delete cur;
				cur = nullptr;
			}
			//左为空但右不为空,拿右节点代替
			else if (!cur->_left && cur->_right) 
			{
				Node* subR = cur->_right;
				delete cur;
				cur = subR;
			}
			//左不为空右为空，拿左节点代替
			else if (cur->_left && !cur->_right) 
			{
				Node* subL = cur->_left;
				delete cur;
				cur = subL;
			}
			//左右都不为空
			else 
			{
				Node* pre = nullptr;
				//找右子树的最左节点，并且路径上的值--
				Node* des = cur->_right;
				des->_size--;
				while (des->_left) 
				{
					pre = des;
					des = des->_left;
					des->_size--;
				}
				//替换法删除
				//将des换到头结点，des的位置用右子树替代
				if (pre) 
				{
					pre->_left = des->_right;
					des->_right = cur->_right;
				}
				des->_left = cur->_left;
				//更新size
				des->_size = des->_left->_size + (des->_right ? des->_right->_size : 0) + 1;

				delete cur;
				cur = des;
			}
		}
		//在返回前进行调整
		cur = maintain(cur);

		return cur;//返回新头部
	}

	//删除key节点
	void erase(const K& key) 
	{
		Node* lastNode = findLastIndex(key);
		if (lastNode)
			_root = deleteNode(_root, key);
		else 
		{
			return;
		}
	}
	//在搜索树中找key节点
	Node* findLastIndex(const K& key)
	{
		Node* pre = _root;
		Node* cur = _root;
		while (cur != nullptr) 
		{
			pre = cur;
			if (cur->_kv.first == key) 
			{
				break;
			}
			else if (cur->_kv.first > key) 
			{
				cur = cur->_left;
			}
			else 
			{
				cur = cur->_right;
			}
		}
		return pre;
	}
	//找到比key大的最小的节点
	Node* findLastNoSmallIndex(const K& key) 
	{
		Node* ans = nullptr;
		Node* cur = _root;
		while (cur != nullptr) 
		{
			if (cur->_kv.first == key) 
			{
				ans = cur;
				break;
			}
			else if (cur->_kv.first > key) 
			{
				ans = cur;
				cur = cur->_left;
			}
			else 
			{
				cur = cur->_right;
			}
		}
		return ans;
	}
	//找到比key小的最大的节点
	Node* findLastNoBigIndex(const K& key)
	{
		Node* ans = nullptr;
		Node* cur = _root;
		while (cur != nullptr) 
		{
			if (cur->_kv.first == key) 
			{
				ans = cur;
				break;
			}
			else if (cur->_kv.first > key) 
			{
				cur = cur->_left;
			}
			else 
			{
				ans = cur;
				cur = cur->_right;
			}
		}
		return ans;
	}
	//判断key是否在树中
	bool  containsKey(const K& key)
	{

		Node* lastNode = findLastIndex(key);
		return lastNode && lastNode->_kv.first == key ? true : false;
	}
	//中序遍历
	void _Inorder(Node*& root) 
	{
		if (!root)return;
		_Inorder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_Inorder(root->_right);
	}
	void Inorder() 
	{
		_Inorder(_root);
	}

private:
	Node* _root = nullptr;
};