目录
一、BST概念
前几天学习了堆排序,其实堆排序用到的结构就是二叉树。
那么BST是满足如下规则的二叉树:
树中的任意结点,左子树的值都小于结点的,右子树的值都大于结点的(左小右大)
二、BST的查找、插入和遍历
1、查找
遵循BST“左小右大”的原则,查询时从根结点向下依次查找各个子树,直到 子树为空 或 已查询到 为止。否则设置的对比current结点将一直与目标值比较,小于当前结点时赋给current.left,大于当前结点时赋给current.right。
2、插入
设置一个parent结点(新元素的父结点)和current结点(定位结点)。如果树为空,就使用新元素创造一个新的根结点。否则遍历寻找新元素结点的父结点的位置,接下来的操作就和“查找”操作很像了。定位父结点成功后比较新元素和父元素大小,判断标准依旧是左大右小。
3、遍历
树的遍历方法主要有前序(preorder)、中序(inorder)、后序(postorder)、深度优先和广度优先。以下面这个二叉树为例:
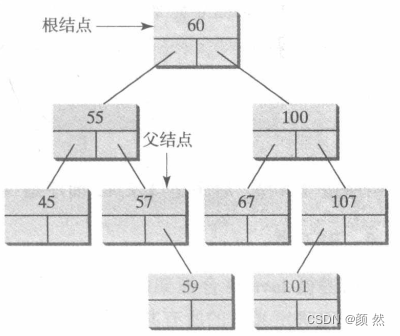
(1)前序
访问current?-> 递归访问current.left -> 递归访问current.right
遍历为:60 55 45 57 59 100 67 107 101
(2)中序(递增显示)
递归访问current.left -> 访问current -> 递归访问current.right
遍历为:45 55 57 59 60 67 100 101 107(注意是先101才107 因为左边优先级大于右边)
(3)后序
递归访问current.left -> 递归访问current.right -> 访问current
遍历为:45 59 57 55 67 101 107 100 60
(4)深度优先(DFS)
访问root -> 任意顺序递归访问其left和right(前序遍历算是深度优先遍历的一个特例)
(5)广度优先(BFS)
逐层访问。访问root -> 从左往右访问其子结点 -> 再从左往右访问其孙结点2
遍历为:60 55 100 45 57 67 107 59 101
4、删除
删除操作要比插入操作复杂很多。删除结点之前需要定位current和current,然后分为有current.left和无current.left两个情况:
(1)无左子结点时
当current只有右子结点时,只需要:
- 将current.right和parent连接
- 删除current
(2)有左子结点时
找出current左子树中的最大元素记为rightMost(注意rightMost可能有左结点但绝对没有右结点),记rightMost的父结点为parentOfrightMost。接下来:
- 替换current中的元素值为rightMost
- 然后连接parentOfrightMost和rightMost.left
- 最后删除rightMost
三、定义一个树接口
我们定义Tree接口为Collection接口的子类:
import java.util.Collection;
public interface Tree<E> extends Collection<E> {
public boolean search(E e);
public boolean insert(E e);
public boolean delete(E e);
public int getSize();
public default void inorder(){
}
public default void postorder(){
}
public default void preorder(){
}
// 重写Collection中定义的方法
@Override
public default boolean isEmpty(){
return size() == 0;
}
@Override
public default boolean contains(Object e){
return search((E)e);
}
@Override
public default boolean add(E e){
return insert(e);
}
@Override
public default boolean remove(Object e){
return delete((E)e);
}
@Override
public default int size(){
return getSize();
}
@Override
public default boolean containsAll(Collection<?> c){
return false;
}
@Override
public default boolean addAll(Collection<? extends E> c){
return false;
}
@Override
public default boolean removeAll(Collection<?> c){
return false;
}
@Override
public default boolean retainAll(Collection<?> c){
return false;
}
@Override
public default Object[] toArray(){
return null;
}
@Override
public default <T> T[] toArray(T[] array){
return null;
}
}四、实现BST类?
class BST<E extends Comparable<E>> implements Tree<E>{
protected TreeNode<E> root;
protected int size = 0;
public BST(){
}
public BST(E[] objects) {
for(int i =0; i < objects.length; i++) {
add(objects[i]);
}
}
// 查找
@Override
public boolean search(E e){
TreeNode current = root;
while(current != null){ //不为空时->
if(e.compareTo((E) current.element) < 0){ // 小于->
current = current.left; //指到left->
}else if(e.compareTo((E) current.element) > 0){ // 大于->
current = current.right; //指到right->
}else return true; // 相同即找到
}
return false; // 没找到
}
/* 递归search
public boolean search(E e) {
return search(root, e);
}
public boolean search(TreeNode<E> root, E e) {
if (root == null)
return false;
else if (e.compareTo(root.element) < 0)
return search(root.left, e);
else if (e.compareTo(root.element) > 0)
return search(root.right, e);
else
return true;
}
* */
// 插入
@Override
public boolean insert(E e){
if(root == null){
root = createNewNode(e); //如果树为空,创建一个新的根结点
}else {
// 否则寻找新元素父节点的位置
TreeNode<E> parent = null;
TreeNode<E> current = root;
while(current != null){
if(e.compareTo(current.element) < 0){
parent = current;
current = current.left;
}else if(e.compareTo(current.element) > 0){
parent = current;
current = current.left;
}else return false;
}
// 链接父结点
if(e.compareTo(parent.element) < 0)
parent.left = createNewNode(e);
else
parent.right = createNewNode(e);
}
size++;
return true;
}
protected TreeNode<E> createNewNode(E e){
return new TreeNode<>(e);
}
// 中序遍历
@Override
public void inorder(){
inorder(root);
}
protected void inorder(TreeNode<E> root){
if(root == null){ // 树为空时结束递归
return;
}
inorder(root.left); //递归左结点
System.out.print(root.element + " "); // 中间结点
inorder(root.right); // 递归右结点
}
// 后序遍历
@Override
public void postorder(){
postorder(root);
}
protected void postorder(TreeNode<E> root){
if(root == null){
return;
}
postorder(root.left);
postorder(root.right);
System.out.print(root.element + " ");
}
// 前序遍历
public void preorder(){
preorder(root);
}
protected void preorder(TreeNode<E> root){
if(root == null){
return ;
}
System.out.print(root.element + " ");
preorder(root.left);
preorder(root.right);
}
// 树结点class
public static class TreeNode<E>{
protected E element;
protected TreeNode<E> left;
protected TreeNode<E> right;
public TreeNode(E e){
element = e;
}
}
@Override
public int getSize(){
return size;
}
public TreeNode<E> getRoot(){
return root;
}
// 以数组线性表返回结点路径
public java.util.ArrayList<TreeNode<E>> path(E e){
java.util.ArrayList<TreeNode<E>> list = new java.util.ArrayList<>();
TreeNode<E> current = root;
while(current != null){
list.add(current);
if(e.compareTo(current.element) < 0){
current = current.left;
}else if(e.compareTo(current.element) > 0){
current = current.right;
}else break;
}
return list;
}
/**删除*/
@Override
public boolean delete(E e){
TreeNode<E> parent = null;
TreeNode<E> current = root;
// 定位current和parent
while(current != null){
if(e.compareTo(current.element) < 0){
parent = current;
current = current.left;
}else if(e.compareTo(current.element) > 0){
parent = current;
current = current.right;
}else break;
}
if(current == null){
return false; // 结点不在树中
}
// 1、无左子结点
if(current.left == null){
if(parent == null){
root = current.right; // 没有父结点 就设为根结点
}else {
if(e.compareTo(parent.element) < 0){ // 删除current结点
parent.left = current.right;
}else {
parent.right = current.right;
}
}
}else{ // 2、有左子结点
TreeNode<E> parentOfRightMost = current;
TreeNode<E> rightMost = current.left;
// 定位rightMost和parentOfRightMost
while (rightMost.right != null){
parentOfRightMost = rightMost;
rightMost = rightMost.right;
}
current.element = rightMost.element; // 用rightMost替换current
// 删除rightMost结点
if(parentOfRightMost.right == rightMost){
parentOfRightMost.right = rightMost.left;
}else{
parentOfRightMost.left = rightMost.left;
}
}
size--;
return true;
}
// 遍历迭代器
@Override
public java.util.Iterator<E> iterator() {
return new InorderIterator();
}
private class InorderIterator implements java.util.Iterator<E>{
private java.util.ArrayList<E> list = new java.util.ArrayList<>();
private int current = 0;
public InorderIterator(){
inorder();
}
private void inorder(){
inorder(root);
}
private void inorder(TreeNode<E> root){
if(root == null){
return;
}
inorder(root.left);
list.add(root.element);
inorder(root.right);
}
@Override
public boolean hasNext(){
if(current < list.size()){
return true;
}
return false;
}
@Override
public E next(){
return list.get(current++);
}
@Override
public void remove(){
if(current == 0){
throw new IllegalStateException();
}
delete(list.get(--current));
list.clear();
inorder();
}
}
@Override
public void clear(){
root = null;
size = 0;
}
}五、数据压缩:哈夫曼编码
哈夫曼编码中的字符编码基于字符出现的次数使用二叉树构建。使用贪心算法,算法总是选择具有最小权重的两棵树,并且创造一个新的父结点:
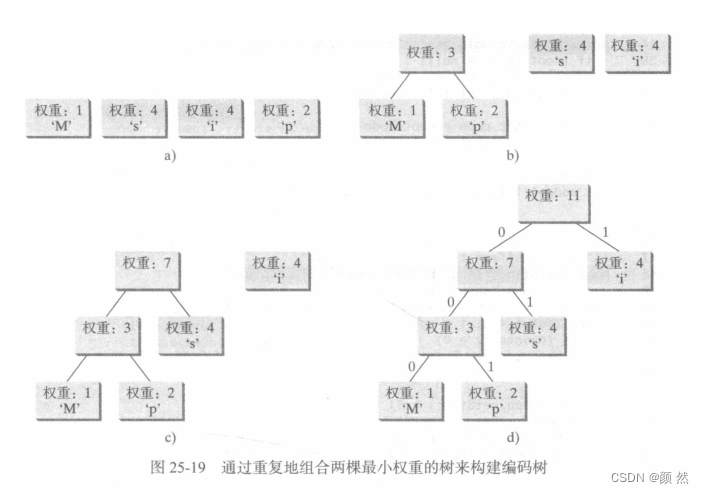
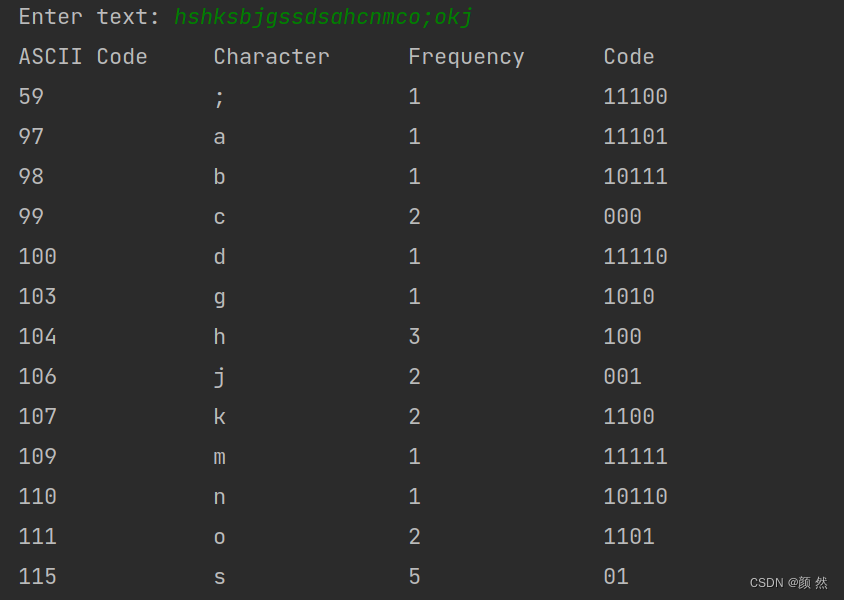
?接下来编写一个程序,用户输入字符串,程序将会输出每个字符出现的次数以及其哈夫曼编码:
import java.util.Scanner;
public class HuffmanCode {
public static void main(String[] args){
Scanner input = new Scanner(System.in);
System.out.print("Enter text: ");
String text = input.nextLine();
// 计算字符出现次数
int[] counts = getCharacterFrequency(text);
System.out.printf("%-15s%-15s%-15s%-15s\n","ASCII Code","Character","Frequency","Code");
// 基于counts得到哈夫曼树
Tree tree = getHuffmanTree(counts);
String[] codes = getCode(tree.root);
for(int i = 0; i < codes.length; i++){
if(counts[i] != 0){
System.out.printf("%-15s%-15s%-15s%-15s\n",i, (char)i + "",counts[i],codes[i]);
}
}
}
// 获取每个叶子结点中字符的编码
public static String[] getCode(Tree.Node root) {
if(root == null){
return null;
}
String[] codes = new String[2 *128];
assignCode(root,codes);
return codes;
}
// 给树中每个结点赋予编码
private static void assignCode(Tree.Node root, String[] codes){
if(root.left != null){
root.left.code = root.code + "0";
assignCode(root.left, codes);
root.right.code = root.code + "1";
assignCode(root.right,codes);
}else {
codes[(int) root.element] = root.code;
}
}
// 返回一颗哈夫曼树
public static Tree getHuffmanTree(int[] counts){
// 创建单结点树并添加到堆中
Heap<Tree> heap = new Heap<>();
for(int i = 0; i < counts.length; i++){
if(counts[i] > 0){
heap.add(new Tree(counts[i],(char)i));
}
}
// while迭代
while(heap.getSize() > 1){
Tree t1 = heap.remove(); //每次将权重最小的两个子树从堆中删除
Tree t2 = heap.remove();
heap.add(new Tree(t1, t2)); //t1,t2组合成新树。接着添加新树到堆中
}
return heap.remove();
}
// 创建一个数组计算256个ASCII字符出现的次数
public static int[] getCharacterFrequency(String text){
int[] counts = new int[256];
for(int i = 0; i < text.length(); i++){
counts[(int)text.charAt(i)]++;
}
return counts;
}
public static class Tree implements Comparable<Tree>{
Node root;
public Tree(Tree t1, Tree t2){
root = new Node();
root.left = t1.root;
root.right = t2.root;
root.weight = t1.root.weight + t2.root.weight;
}
public Tree(int weight, char element) {
root = new Node(weight, element);
}
@Override
public int compareTo(Tree t) {
if(root.weight < t.root.weight){
return 1;
}else if(root.weight == t.root.weight){
return 0;
}else return -1;
}
public class Node{
char element;
int weight;
Node left;
Node right;
String code = "";
public Node() {
}
public Node(int weight, char element){
this.weight = weight;
this.element = element;
}
}
}
}运行结果如下:?