动态规划图像压缩算法
看了很多博客,感觉对于b[i]数组(本文中的bitnum数组)的定义都不是很正确,自己思考了很久,记录一下!
①递归算法的实现
设置递归函数compress(px, bitnum, length, index)
- 参数px:输入的数组( i从0开始,0 =< px[i] <= 255)
- 参数bitnum:bitnum[i]表示存储px[i]所需的存储位数(按照其他博客的意思是表示px[0…i]最优分段中最后一段中的最大存储位数,但这样的定义很明显与他们的代码不相符)
- 参数length:length[i]表示以px[0…i]的最优分段中的最后一段的像素点的个数
- 参数index:表示要将px[0…index]进行最优分段
//length[i]: px[0..i]最优分段中最后一段的像素点个数
//bitnum[i]: px[i]的存储位数
int compress(const vector<int>& px, vector<int>& bitnum, vector<int>& length, int index) {
if (index < 0) return 0;
bitnum[index] = ceil(log(px[index] + 1) / log(2));
int bmax = bitnum[index];
int pre = compress(px, bitnum, length, index - 1);
int ans = pre + bmax + 11;
length[index] = 1;
for (int k = 2; k <= index + 1 && k <= 255; ++k) {
pre = compress(px, bitnum, length, index - k);
if (bmax < bitnum[index - k + 1]) {
bmax = bitnum[index - k + 1];
}
if (pre + k * bmax + 11 < ans) {
ans = pre + k * bmax + 11;
//bitnum[index] = bmax;
length[index] = k;
}
}
return ans;
}
以上代码有很多的重复计算
②动态规划算法实现
动态规划相较于递归最明显的好处之一就是避免了重复计算
根据递归代码比较容易将其改为动态规划算法:
int main() {
int n;
cin >> n;
vector<int> px(n);
for (int i = 0; i < n; ++i) {
cin >> px[i];
}
vector<int> length(n);
vector<int> bitnum(n);
vector<int> dp(n);
for (int i = 0; i < n; ++i) {
bitnum[i] = ceil(log(px[i] + 1) / log(2));
int bmax = bitnum[i];
length[i] = 1;
if (i == 0) {
dp[i] = 0 + bmax + 11;
}
else {
dp[i] = dp[i - 1] + bmax + 11;
}
for (int k = 2; k <= i + 1 && k <= 255; ++k) {
if (bmax < bitnum[i - k + 1]) {
bmax = bitnum[i - k + 1];
}
if ((i - k < 0 ? 0 : dp[i - k]) + k * bmax + 11 < dp[i]) {
dp[i] = (i - k < 0 ? 0 : dp[i - k]) + k * bmax + 11;
length[i] = k;
}
}
}
//cout << "the optimal value is " << compress(px, bitnum, length, n - 1) << endl;
cout << "the optimal value is " << dp[n - 1] << endl;
return 0;
}
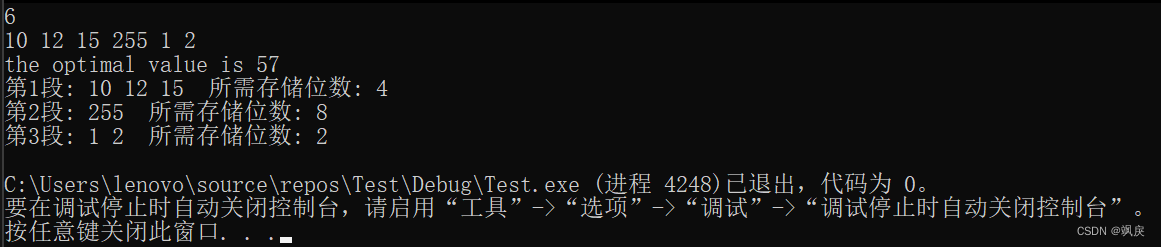
输出最优分段结果
此时length[i]存储px[0…i]最优分段中的最后一段的像素点的个数
bitnum[i]存储px[i]所需要的存储位数
根据这两个信息使用递归回溯算法输出结果:
int traceback(const vector<int>& v, const vector<int>& bitnum, const vector<int>& length, int index) {
if (index < 0) {
return 0;
}
int prenum = traceback(v, bitnum, length, index - length[index]);
int start = index - length[index] + 1;
int maxn = INT_MIN;
cout << "第" << prenum + 1 << "段: ";
for (int i = start; i <= index; i++) {
cout << v[i] << " ";
maxn = max(maxn, bitnum[i]);
}
cout << " 所需存储位数: " << maxn << endl;
return prenum + 1;
}
最终代码
#include<iostream>
#include<vector>
#include<limits.h>
#include<algorithm>
using namespace std;
//length[i]: px[0..i]最优分段中最后一段的像素点个数
//bitnum[i]: px[i]的存储位数
//int compress(const vector<int>& px, vector<int>& bitnum, vector<int>& length, int index) {
// if (index < 0) return 0;
// bitnum[index] = ceil(log(px[index] + 1) / log(2));
// int bmax = bitnum[index];
// int pre = compress(px, bitnum, length, index - 1);
// int ans = pre + bmax + 11;
// length[index] = 1;
// for (int k = 2; k <= index + 1 && k <= 255; ++k) {
// pre = compress(px, bitnum, length, index - k);
// if (bmax < bitnum[index - k + 1]) {
// bmax = bitnum[index - k + 1];
// }
// if (pre + k * bmax + 11 < ans) {
// ans = pre + k * bmax + 11;
// //bitnum[index] = bmax;
// length[index] = k;
// }
// }
// return ans;
//}
int traceback(const vector<int>& v, const vector<int>& bitnum, const vector<int>& length, int index) {
if (index < 0) {
return 0;
}
int prenum = traceback(v, bitnum, length, index - length[index]);
int start = index - length[index] + 1;
int maxn = INT_MIN;
cout << "第" << prenum + 1 << "段: ";
for (int i = start; i <= index; i++) {
cout << v[i] << " ";
maxn = max(maxn, bitnum[i]);
}
cout << " 所需存储位数: " << maxn << endl;
return prenum + 1;
}
int main() {
int n;
cin >> n;
vector<int> px(n);
for (int i = 0; i < n; ++i) {
cin >> px[i];
}
vector<int> length(n);
vector<int> bitnum(n);
vector<int> dp(n);
for (int i = 0; i < n; ++i) {
bitnum[i] = ceil(log(px[i] + 1) / log(2));
int bmax = bitnum[i];
length[i] = 1;
if (i == 0) {
dp[i] = 0 + bmax + 11;
}
else {
dp[i] = dp[i - 1] + bmax + 11;
}
for (int k = 2; k <= i + 1 && k <= 255; ++k) {
if (bmax < bitnum[i - k + 1]) {
bmax = bitnum[i - k + 1];
}
if ((i - k < 0 ? 0 : dp[i - k]) + k * bmax + 11 < dp[i]) {
dp[i] = (i - k < 0 ? 0 : dp[i - k]) + k * bmax + 11;
length[i] = k;
}
}
}
//cout << "the optimal value is " << compress(px, bitnum, length, n - 1) << endl;
cout << "the optimal value is " << dp[n - 1] << endl;
traceback(px, bitnum, length, n - 1);
return 0;
}