[数据结构与算法]1162 Postfix Expression

Given a syntax tree (binary), you are supposed to output the corresponding postfix expression, with parentheses reflecting the precedences of the operators.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤?20) which is the total number of nodes in the syntax tree. Then N lines follow, each gives the information of a node (the?i-th line corresponds to the?i-th node) in the format:

data left_child right_child

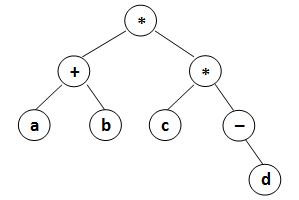
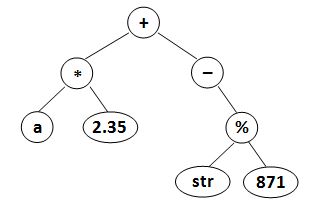
where?data?is a string of no more than 10 characters,?left_child?and?right_child?are the indices of this node's left and right children, respectively. The nodes are indexed from 1 to N. The NULL link is represented by??1. The figures 1 and 2 correspond to the samples 1 and 2, respectively.

Output Specification:

For each case, print in a line the postfix expression, with parentheses reflecting the precedences of the operators.There must be no space between any symbols.

Sample Input 1:

8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1

Sample Output 1:

(((a)(b)+)((c)(-(d))*)*)

Sample Input 2:

8
2.35 -1 -1
* 6 1
- -1 4
% 7 8
+ 2 3
a -1 -1
str -1 -1
871 -1 -1

Sample Output 2:

(((a)(2.35)*)(-((str)(871)%))+)

题目大意?

给定一个二叉表达式树，请你输出相应的后缀表达式，要求使用括号反映运算符的优先级

注意点

三种情况：

①左右孩子都不存在时 ，直接访问当前节点

②左右孩子都存在时 进行后序遍历 即：左->右->根

③左孩子不存在右孩子存在时，进行先序遍历即 ：根->右?

AC代码

/*
* @Author: Spare Lin
* @Project: AcWing2022
* @Date: 2022/6/28 14:28
* @Description: PAT (Advanced Level) 1162 Postfix Expression
*/

#include <iostream>
#include <algorithm>

using namespace std;

const int MAXN = 25;

typedef struct {
    int l, r;   //左右孩子
    string v;   //权值
} Node;

Node node[MAXN];
int n, root, flag[MAXN];

void dfs(int index) {
    cout << '(';
    //左右孩子都不存在 直接输出节点权值
    if (node[index].l == -1 && node[index].r == -1) {
        cout << node[index].v;
    }
    //左右孩子都存在 则进行后序遍历
    else if (node[index].l != -1 && node[index].r != -1) {
        dfs(node[index].l);
        dfs(node[index].r);
        cout << node[index].v;
    }
    //样例中的-作为负号时 进行先序遍历 即左孩子不存在 右孩子存在 先访问节点权值再访问右孩子
    else {
        cout << node[index].v;
        dfs(node[index].r);
    }
    cout << ')';
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> node[i].v >> node[i].l >> node[i].r;
        if (node[i].l != -1) flag[node[i].l] = 1;  //当前结点左孩子是否存在
        if (node[i].r != -1) flag[node[i].r] = 1;  //当前结点右孩子是否存在
    }
    //遍历找根节点
    for (int i = 1; i <= n; ++i) {
        if (flag[i] == 0) {
            root = i;
        }
    }

    dfs(root);

    return 0;
}

?